Обратные тригонометрические функции
Определение обратных тригонометрических функций
Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin x, при заданном , имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x такой корень, то и x + 2πn (где n целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны. Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin x. Если ограничить аргумент x интервалом , то на нем функция y = sin x монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin y.
Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.
- Арксинус ( y = arcsin x )
- – это функция, обратная к синусу ( x = sin y ), имеющая область определения и множество значений .
- Арккосинус ( y = arccos x )
- – это функция, обратная к косинусу ( x = cos y ), имеющая область определения и множество значений .
- Арктангенс ( y = arctg x )
- – это функция, обратная к тангенсу ( x = tg y ), имеющая область определения и множество значений .
- Арккотангенс ( y = arcctg x )
- – это функция, обратная к котангенсу ( x = ctg y ), имеющая область определения и множество значений .
Графики обратных тригонометрических функций
Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x. См. разделы Синус, косинус, Тангенс, котангенс.

y = arcsin x

y = arccos x

y = arctg x

y = arcctg x
Основные формулы
Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.
arcsin(sin x) = x при
sin(arcsin x) = x
arccos(cos x) = x при
cos(arccos x) = x
arctg(tg x) = x при
tg(arctg x) = x
arcctg(ctg x) = x при
ctg(arcctg x) = x
Формулы, связывающие обратные тригонометрические функции
См. также: Вывод формул обратных тригонометрических функцийФормулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
при
при
при
при
при
при
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано:
Арксинус, арккосинус — свойства, графики, формулы
Арксинус, arcsin
Определение и обозначения
- Арксинус ( y = arcsin x )
- – это функция, обратная к синусу ( x = sin y ). Он имеет область определения –1 ≤ x ≤ 1 и множество значений –π/2 ≤ y ≤ π/2.
sin(arcsin x) = x ;
arcsin(sin x) = x .
Арксинус иногда обозначают так:
.
График функции арксинус

График функции y = arcsin x
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccos
Определение и обозначения
- Арккосинус ( y = arccos x )
- – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения –1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π.
cos(arccos x) = x ;
arccos(cos x) = x .
Арккосинус иногда обозначают так:
.
График функции арккосинус

График функции y = arccos x
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin x
Функция арккосинус не является четной или нечетной:
arccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) = π – arccos x ≠ ± arccos x
Свойства — экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | – 1 ≤ x ≤ 1 | – 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
| x | arcsin x | arccos x | ||
| град. | рад. | град. | рад. | |
| – 1 | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 | |
≈ 0,7071067811865476
≈ 0,8660254037844386
Формулы
См. также: Вывод формул обратных тригонометрических функцийФормулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
Выражения через логарифм, комплексные числа
См. также: Вывод формулВыражения через гиперболические функции
Производные
;
.
См. Вывод производных арксинуса и арккосинуса > > >
Производные высших порядков:
,
где – многочлен степени . Он определяется по формулам:
;
;
.
См. Вывод производных высших порядков арксинуса и арккосинуса > > >
Интегралы
Делаем подстановку x = sin t. Интегрируем по частям, учитывая что –π/2 ≤ t ≤ π/2, cos t ≥ 0:
.
Выразим арккосинус через арксинус:
.
Разложение в ряд
При |x| < 1 имеет место следующее разложение:
;
.
Обратные функции
Обратными к арксинусу и арккосинусу являются синус и косинус, соответственно.
Следующие формулы справедливы на всей области определения:
sin(arcsin x) = x
cos(arccos x) = x .
Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin x) = x при
arccos(cos x) = x при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: Изменено:
Основные формулы: арксинус, арккосинус, арктангенс, арккотангенс.
Область определения и множество значений:
Основные тождества:
Значения тригонометрических функций от обратных тригонометрических функций:
Взаимосвязь арксинуса с другими обратными тригонометрическими функциями:
Взаимосвязь арккосинуса с другими обратными тригонометрическими функциями:
Взаимосвязь арктангенса с другими обратными тригонометрическими функциями:
Взаимосвязь арккотангенса с другими обратными тригонометрическими функциями:
Формулы сложения для обратных тригонометрических функций:
|
Обратные тригонометрические функции — это… Что такое Обратные тригонометрические функции?
Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:
- аркси́нус (обозначение: arcsin)
- аркко́синус (обозначение: arccos)
- аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)
- арккота́нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan)
- арксе́канс (обозначение: arcsec)
- арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)
Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin−1 для арксинуса и т. п.; это считается не совсем корректным, так как возможна путаница с возведением функции в степень −1.
Основное соотношение
Функция arcsin
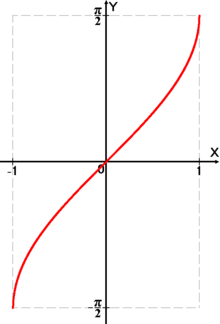 График функции .
График функции .Арксинусом числа m называется такое значение угла x, для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.
Свойства функции arcsin
Получение функции arcsin
Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — . Так как для функции на интервале каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция график которой симметричен графику функции на отрезке относительно прямой
Функция arccos
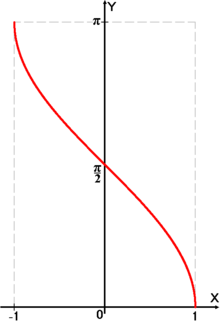 График функции .
График функции .Арккосинусом числа m называется такое значение угла x, для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.
Свойства функции arccos
Получение функции arccos
Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — На этом отрезке строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке существует обратная функция график которой симметричен графику на отрезке относительно прямой
Функция arctg
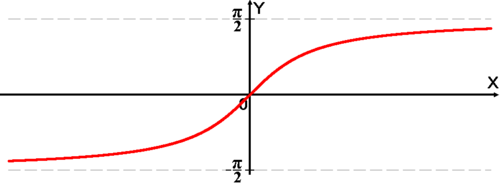 График функции .
График функции .Арктангенсом числа m называется такое значение угла , для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.
Свойства функции arctg
- , при x > 0.
Получение функции arctg
Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — На этом отрезке строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале существует обратная , график которой симметричен графику на отрезке относительно прямой
Функция arcctg
График функции y=arcctg xАрккотангенсом числа m называется такое значение угла x, для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.
Свойства функции arcctg
Получение функции arcctg
Дана функция . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз — . На этом отрезке строго убывает и принимает все свои значения только один раз, следовательно, на интервале существует обратная функция , график которой симметричен графику на отрезке относительно прямой График симметричен к арктангенсу
Функция arcsec
Функция arccosec
Производные от обратных тригонометрических функций
Интегралы от обратных тригонометрических функций
Неопределённые интегралы
Для действительных и комплексных x:
Для действительных x ≥ 1:
- См. также Список интегралов от обратных тригонометрических функций
Интегралы от обратных тригонометрических функций
Неопределённые интегралы
Для действительных и комплексных x:
Для действительных x ≥ 1:
- См. также Список интегралов от обратных тригонометрических функций
Использование в геометрии
Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например с помощью теоремы косинусов.
В прямоугольном треугольнике, эти функции от отношений сторон сразу дают угол:
- α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a)
Связь с натуральным логарифмом
Для вычисления значений обратных тригонометрических функций от комплексного аргумента удобно использовать формулы, выражающие их через натуральный логарифм:
См. также
Ссылки
Арктангенс, арккотангенс — свойства, графики, формулы
Арктангенс, arctg
Определение и обозначения
- Арктангенс ( y = arctg x )
- – это функция, обратная к тангенсу ( x = tg y ). Он имеет область определения и множество значений .
tg(arctg x) = x ;
arctg(tg x) = x .
Арктангенс обозначается так:
.
График функции арктангенс

График функции y = arctg x
График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.
Арккотангенс, arcctg
Определение и обозначения
- Арккотангенс ( y = arcctg x )
- – это функция, обратная к котангенсу ( x = ctg y ). Он имеет область определения и множество значений .
ctg(arcctg x) = x ;
arcctg(ctg x) = x .
Арккотангенс обозначается так:
.
График функции арккотангенс

График функции y = arcctg x
График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккотангенса.
Четность
Функция арктангенс является нечетной:
arctg(–x) = arctg(–tg arctg x) = arctg(tg(–arctg x)) = – arctg x
Функция арккотангенс не является четной или нечетной:
arcctg(–x) = arcctg(–ctg arcctg x) = arcctg(ctg(π–arcctg x)) = π – arcctg x ≠ ± arcctg x.
Свойства – экстремумы, возрастание, убывание
Функции арктангенс и арккотангенс непрерывны на своей области определения, то есть для всех x. (см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.
| y = arctg x | y = arcctg x | |
| Область определения и непрерывность | – ∞ < x < + ∞ | – ∞ < x < + ∞ |
| Множество значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы, минимумы | нет | нет |
| Нули, y = 0 | x = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
| – | π | |
| 0 |
Таблица арктангенсов и арккотангенсов
В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.
| x | arctg x | arcctg x | ||
| град. | рад. | град. | рад. | |
| – ∞ | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – 1 | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 1 | 45° | 45° | ||
| 60° | 30° | |||
| + ∞ | 90° | 0° | 0 | |
≈ 0,5773502691896258
≈ 1,7320508075688772
Формулы
См. также: Вывод формул обратных тригонометрических функцийФормулы суммы и разности
при
при
при
при
при
при
Выражения через логарифм, комплексные числа
См. также: Вывод формул ,
.
Выражения через гиперболические функции
Производные
См. Вывод производных арктангенса и арккотангенса > > >
Производные высших порядков:
Пусть . Тогда производную n-го порядка арктангенса можно представить одним из следующих способов:
;
.
Символ означает мнимую часть стоящего следом выражения.
См. Вывод производных высших порядков арктангенса и арккотангенса > > >
Там же даны формулы производных первых пяти порядков.
Аналогично для арккотангенса. Пусть . Тогда
;
.
Интегралы
Делаем подстановку x = tg t и интегрируем по частям:
;
;
;
Выразим арккотангенс через арктангенс:
.
Разложение в степенной ряд
При |x| ≤ 1 имеет место следующее разложение:
;
.
Обратные функции
Обратными к арктангенсу и арккотангенсу являются тангенс и котангенс, соответственно.
Следующие формулы справедливы на всей области определения:
tg(arctg x) = x
ctg(arcctg x) = x .
Следующие формулы справедливы только на множестве значений арктангенса и арккотангенса:
arctg(tg x) = x при
arcctg(ctg x) = x при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: Изменено:
Свойства обратных тригонометрических функций
- Главная
- Справочник
- Тригонометрия
- Свойства обратных тригонометрических функций
Так как геометрически значение обратной тригонометрической функции связано с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку, то названия обратных тригонометрических функций образуются следующим образом: приставка «арк-» (от латинского arc — дуга) + соответствующие им названия тригонометрических функций.
Арксинус
Арксинусом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \sin \alpha=a,\;|a|\leqslant 1,\;\alpha\in[-\frac{\pi}{2};\frac{\pi}{2}]. \)
- Областью определения функции арксинус является отрезок \( [-1;1]. \)
- Областью значений функции арксинус является отрезок \( [-\frac{\pi}{2};\frac{\pi}{2}]. \)
- Арксинус строго возрастающая функция.
- \( \sin \left (\arcsin a \right )=a,\;|a|\leqslant 1. \)
- \( \arcsin\left (\sin \alpha \right )=\alpha,\;\alpha\in[-\frac{\pi}{2};\frac{\pi}{2}]. \)
- Арксинус является нечетной функцией: \( \arcsin(-a)=-\arcsin a,\;|a| \leqslant 1. \)
- \( \arcsin a>0,\;a\in(0;1]. \)
- \( \arcsin a=0,\;a=0. \)
- \( \arcsin a<0,\;a\in[-1;0). \)
Арккосинус
Арккосинусом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \cos \alpha=a,\;|a|\leqslant 1,\;\alpha\in[0;\pi]. \)
- Областью определения функции арккосинус является отрезок \( [-1;1]. \)
- Областью значений функции арккосинус является отрезок \( [0;\pi]. \)
- Арккосинус строго убывающая функция.
- \( \cos \left (\arccos a \right )=a,\;|a|\leqslant 1. \)
- \( \arccos\left (\cos \alpha\right )=\alpha,\;\alpha\in[0;\pi]. \)
- Арккосинус является индифферентной функцией: \( \arccos (-a)=\pi-\arccos a,\;|a|\leqslant 1. \) Функция центрально-симметрична относительно точки \( \left ( 0;\frac{\pi}{2} \right ). \)
- \( \arccos a>0,\;a\in[-1;1). \)
- \( \arccos a=0,\;a=1. \)
Арктангенс
Арктангенсом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \text{tg}\, \alpha=a,\;a\in\mathbb{R},\;\alpha\in\left (-\frac{\pi}{2};\frac{\pi}{2} \right ). \)
- Областью определения функции арктангенс является вся числовая прямая: \( \mathbb{R}. \)
- Областью значений функции арктангенс является интервал \( \left (-\frac{\pi}{2};\frac{\pi}{2} \right ). \)
- Арктангенс строго возрастающая функция.
- \( \text{tg}\left (\text{arctg}\,a \right ) =a,\;a\in\mathbb{R}. \)
- \( \text{arctg}\left (\text{tg}\,\alpha \right ) =\alpha,\;\alpha\in\left ( -\frac{\pi}{2};\frac{\pi}{2} \right ). \)
- Арктангенс является нечетной функцией: \( \text{arctg}\left (-a \right ) =-\text{arctg}\,a,\;a\in\mathbb{R}. \)
- \( \text{arctg}\,a>0,\;a\in(0;\infty ). \)
- \( \text{arctg}\,a=0,\;a=0. \)
- \( \text{arctg}\,a<0,\;a\in(-\infty;0). \)
Арккотангенс
Арккотангенсом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \text{ctg}\, \alpha=a,\;a\in\mathbb{R},\;\alpha\in\left (0;\pi \right ). \)
- Областью определения функции арккотангенс является вся числовая прямая: \( \mathbb{R}. \)
- Областью значений функции арккотангенс является интервал \( \left (0;\pi \right ). \)
- Арккотангенс строго убывающая функция.
- \( \text{ctg}\left (\text{arcctg}\,a \right ) =a,\;a\in\mathbb{R}. \)
- \( \text{arcctg}\left (\text{ctg}\,\alpha \right ) =\alpha,\;\alpha\in\left (0;\pi \right ). \)
- Арккотангенс является индифферентной функцией: \( \text{arcctg}\left (-a \right ) =\pi-\text{arcctg}\,a,\;a\in\mathbb{R}. \) Функция центрально-симметрична относительно точки \( \left ( 0;\frac{\pi}{2} \right ). \)
- \( \text{arcctg}\,a>0,\;a\in\mathbb{R}. \)
Основные соотношения
- \( \arcsin a+\arccos a=\frac{\pi}{2},\;|a|\leqslant 1. \)
- \( \text{arctg}\,a+\text{arcctg}\,a=\frac{\pi}{2},\;a\in\mathbb{R}. \)
Решение простейших тригонометрических уравнений
В общем виде
\( \sin x=a,\;|a|\leqslant 1\Rightarrow x=(-1)^k\arcsin\,a+\pi k,\;k\in\mathbb{Z} \)
или \( \left[\begin{matrix} x&=&\arcsin\,a+2\pi k,&\;k\in\mathbb{Z}\\ x&=&\pi-\arcsin\,a+2\pi l,&\;l\in\mathbb{Z} \end{matrix}\right. \)
\( \cos x=a,\;|a|\leqslant 1\Rightarrow x=\pm\arccos\,a+2\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=a,\;a\in\mathbb{R}\Rightarrow x=\text{arctg}\,a+\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=a,\;a\in\mathbb{R}\Rightarrow x=\text{arcctg}\,a+\pi k,\;k\in\mathbb{Z} \)
Частные случаи
\( \sin x=0\Rightarrow x=\pi k,\;k\in\mathbb{Z} \)
\( \cos x=0\Rightarrow x=\frac{\pi}{2}+\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=0\Rightarrow x=\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=0\Rightarrow x=\frac{\pi}{2}+\pi k,\;k\in\mathbb{Z} \)
\( \sin x=1\Rightarrow x=\frac{\pi}{2}+2\pi k,\;k\in\mathbb{Z} \)
\( \cos x=1\Rightarrow x=2\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=1\Rightarrow x=\frac{\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=1\Rightarrow x=\frac{\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
\( \sin x=-1\Rightarrow x=-\frac{\pi}{2}+2\pi k,\;k\in\mathbb{Z} \)
\( \cos x=-1\Rightarrow x=\pi+2\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=-1\Rightarrow x=-\frac{\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=-1\Rightarrow x=\frac{3\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Разбираемся в терминологии: HDMI ARC и eARC
5-09-2019, 14:32
Время прочтения:


Предназначение HDMI ARC и HDMI eARC
Современные телевизоры оснащаются технологией HDMI. О её наличии можно судить по ярлыкам на коробке ТВ, по разъемам и меню настроек. По HDMI проводам на телевизор поступают звуки с разных внешних устройств (приставки, проигрыватели и пр.). Однако он же дает возможность захватывать аудиосигнал самой бытовой техники. Это делается за счет технологии ARC.
HDMI ARC
Технология HDMI пришла на смену SCART. Определенный момент времени она позволяла подключать ТВ к различным внешним устройствам. Однако первое время такие порты были только входными. Т.е., телевизор мог принимать сигналы от приставок, игровых консолей и прочих внешних устройств.
Для отправки аудиосигнала на эти устройства требуется выделенный порт. Вот для этого и требуется технология HDMI ARC. Это, так сказать, продвинутая версия HDMI. К тому же, она может еще и принимать сигналы.
Эта технология позволяет ликвидировать проблемы с синхронизацией губ. Они имели место при использовании оптических/коаксиальных проводов. Кроме того, в современных комплексах имеется настройка CEC. Она дает возможность с помощью одного пульта управлять не только ТВ, но и прочими подключенными устройствами. Так вот, HDMI ARC способна функционировать и с CEC.
Один пульт плюс отсутствие дополнительных проводов. Удобно, комфортно и внешне все выглядит прекрасно. Можно сказать, что технология ARC является «убийцей кабелей». Плюс — реверсивный аудиоканал позволяет на 100% использовать возможности звуковой системы.
Есть ли недостатки?
Да, они присутствуют. Производители ТВ могут принимать решения о не включении в стандарт некоторых функций. Они считают их лишними и/или ненужными. Вот и получается нестандартный стандарт, что приводит к проблемам, когда интегрируются устройства разных марок. Например, к ТВ Sony подключается саундбар LG.
Поэтому мы рекомендуем находить информацию в интернете или внимательно изучать руководство. Чтобы потом не разочароваться в звуке. Иначе вы будете ожидать Dolby 5.1, а можете услышать стерео!
Если ваш ТВ поддерживает технологию HDMI ARC, он будет оснащен на панели соответствующим разъемом, HDMI OUT (ARC). Настройки произойдут в авторежиме. Как только вы подключите саундбар к ТВ через нужный разъем, сразу на него пойдет трансляция. Еще в версии HDMI 1.3 отсутствовала проблема синхронизации. А сейчас используются более продвинутые 2.0/2.1. Поэтому передача будет без задержек.
HDMI eARC
Технология HDMI появилась в начале нынешнего столетия. Однако с мощным развитием телевизионной индустрии начали вырастать требования и к качеству аудио. Поэтому в 2013 г. появилась технология HDMI 2.0. Она нужна была для поддержки телевизоров 4К UHD, обладающих частоту обновления в 60 кадров/сек. После обновлений технология стала поддерживать возможности HDR и HLG.
С появлением современных телевизоров требования к 4K-видео и высококачественному аудио еще больше выросли. На рынке появилась версия HDMI 2.1. Она обеспечивает поддержку:
- 4K при 120fps;
- 8K при 60fps;
- Видео 10K.
Пропускная способность HDMI 2.1 до 48 Гбит/сек.
Поэтому и ARC обновилась до расширенной версии eARC. У нее больше пропускной способности. Эта технология – оптимальный вариант для поддержки объемного звука и она обеспечивает высокое качество для разных звуковых форматов:
- Dolby Atmos;
- Dolby TrueHD;
- DTS: X;
- DTS Master.
Т.е., высококачественный аудиосигнал можно будет передавать на ресиверы акустических систем/домашнего кинотеатра. Кабели HDMI способны отправлять/получать звуковой сигнал при скорости в 1 Мбит/сек. У eARC скорость увеличится до 38 раз. Что касается качества, то данная технология способна одновременно транслировать данные для 8 каналов (192 кГц/24 бит).
Представители HDMI Forum заявляют, что новая технология:
- Упростит подключение к ТВ разных компонентов;
- Сделает удобной управление системой;
- Обеспечит высокое качество аудио;
- Будет совместима с новыми форматами.
Телевизоры, поддерживающие eARC
Технологию HDMI 2.1 и eARC поддерживают телевизоры японского производителя Sony и южнокорейской компании LG.
К примеру, у Sony можно отметить серии ТВ AG9, AF9, ZF9 и ZG9. Первые 3 серии имеют разрешение 4К, а последняя – 8К.
Аналогичная ситуация и с телевизорами OLED от LG. Здесь 4 серии (W9, E9, C9, B9) с разрешением 4К и одна (Z9) – с 8К, поддерживают технологию eARC.
Что можем вам посоветовать? Если вас не особо беспокоит eARC, не стоит менять свой старый телевизор. Если же хотите насладиться новыми стандартами прямо сейчас, то предупреждаем, что вам придется изрядно раскошелиться. Во всяком случае, в ближайшие год-два. Технология новая, поэтому телевизоры, оснащенные такими портами, будут стоить дорого.
Обсудить данную статью можно в специальной теме на нашем форуме, будем рады Вас видеть!
Нашли ошибку? Выделите ее и нажмите ctrl+enter
Комментариев: 0