Примеры по математике со скобками
Выполнение тех или иных операций предполагает определённый порядок действий.
4 – 2 + 1 = 3
Если производить действия в порядке их записи, четыре минус два плюс один, результат будет равен трём. Если же вначале сложить 2 и 1 и вычесть данную сумму из 4, то получится цифра 1.
Чтобы указать, в каком порядке нужно выполнять действия применяют скобки.
Действия, заключенные в скобки, выполняются раньше других.
Пример:
(4 – 2) + 1 = 3
5 – (3 + 1) = 1
(3 + 4) × 5 = 7 × 5 = 35
4 + (4 × 5) = 4 + 20 =
Скобки не ставятся в тех случаях если:
1. действия сложения и вычитания, исполняются в последовательности, как они записаны:
действия сложения и вычитания, исполняются в последовательности, как они записаны:
вместо (6 – 2) + 1 = 5 пишут 6 – 2 + 1 = 5
2. внутри скобок совершаются операции умножения или деления:
вместо 2 + (2 × 8) = 18 пишут 2 + 2 × 8 = 18
При расчёте таких выражений, которые либо вовсе не содержат разделительных
1. вначале выполняются операции с цифрами заключенными в скобки, при этом действия умножения и деления делаются в порядке их следования, но ранее, чем сложение и вычитание.
2. Затем, исполняются остающиеся действия, причем опять умножение и деление производятся в порядке их следования, но ранее сложения и вычитания.
Пример:
2 × 5 – 3 ×
сначала выполняется умножения
2 × 5 = 10
3 × 3 = 9
затем выполняется вычитание
10 – 9 = 1
Пример:
22 + 16 : 4 – 4 × (17 – 2 × 7 + 3) + 7 × (3 + 4)
выполнение действий в скобках:
17 – 2 × 7 + 4 = 17 – 14 + 3 = 6
3
4 = 7выполнение остающихся действий:
22 + 16 : 4 – 4 × 6 + 7 × 7 = 22 + 4 – 24 + 49 = 51
Зачастую для указания порядка действий, необходимо применять дополнительные скобки.
Тогда, кроме простых круглых скобок, используют скобки иной формы:
[ ] – квадратные скобки
{ } – фигурные скобки
Вычисление этих выражений реализуется в следующем порядке:
Вначале операции вычисления производятся внутри всех круглых скобок
затем – вычисления внутри всех квадратных скобок
далее – вычисления внутри фигурных скобок
после выполняются остающиеся действия
Пример:
5 + 2 × [14 – 4 × (7 – 5) ] + 36 : (12 – 2 × 3)
выполнение действий в круглых скобках:
7 – 5 = 2
12 – 2 × 3 = 12 – 6 = 6
действия в квадратных скобках
14 – 4 × 2 = 6
выполнение остающихся действий:
5 + 2 × 6 + 36 : 6 = 5 + 12 + 6 = 23
Пример:
{100 – [40 – (35 – 25)]} × 2
Порядок действий:
35 – 25 = 10
40 – 10 = 30
100 – 30 = 70
70 × 2 = 140
Раскрытие скобок
Продолжаем изучать основы алгебры.
Чтобы раскрывать скобки, нужно выучить наизусть два правила. При регулярных занятиях раскрывать скобки можно с закрытыми глазами, и про те правила которые требовалось заучивать наизусть, можно благополучно забыть.
Первое правило раскрытия скобок
Рассмотрим следующее выражение:
8 + (−9 + 3)
Значение данного выражения равно 2. Раскроем скобки в данном выражении. Раскрыть скобки означает избавиться от них, не влияя на значение выражения. То есть после избавления от скобок значение выражения 8 + (−9 + 3) по прежнему должно быть равно двум.
Первое правило раскрытия скобок выглядит следующим образом:
При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.
Итак, мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Этот плюс нужно опустить вместе со скобками. Иными словами, скобки исчезнут вместе с плюсом, который перед ними стоял. А то, что было в скобках запишется без изменений:
Иными словами, скобки исчезнут вместе с плюсом, который перед ними стоял. А то, что было в скобках запишется без изменений:
Мы получили выражение без скобок 8−9+3. Данное выражение равно 2, как и предыдущее выражение со скобками было равно 2.
8 + (−9 + 3) = 2
8 − 9 + 3 = 2
Таким образом, между выражениями 8+(−9+3) и 8−9+3 можно поставить знак равенства, поскольку они равны одному и тому же значению:
8 + (−9 + 3) = 8 − 9 + 3
2 = 2
Пример 2. Раскрыть скобки в выражении 3 + (−1 − 4)
Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках останется без изменений:
3 + (−1 − 4) = 3 − 1 − 4
Пример 3. Раскрыть скобки в выражении 2 + (−1)
Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках останется без изменений:
2 + (−1) = 2 − 1
В данном примере раскрытие скобок стало своего рода обратной операцией замене вычитания сложением. Как это понимать?
Как это понимать?
В выражении 2 − 1 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 2 + (−1). Но если в выражении 2 + (−1) раскрыть скобки, то получится изначальное 2 − 1.
Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после каких-нибудь преобразований. То есть избавить его от скобок и сделать проще.
Например, упростим выражение 2a + a− 5b + b.
Чтобы упростить данное выражение, можно привести подобные слагаемые. Напомним, что для приведения подобных слагаемых, нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:
Получили выражение 3a + (−4b). В этом выражении раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок, то есть опускаем скобки вместе с плюсом, который стоит перед этими скобками:
3a + (−4b) = 3a − 4b
Таким образом, выражение 2a+a−5b+b упрощается до 3a−4b.
2 + (−3 + 1) + 3 + (−6)
Здесь два места, где нужно раскрыть скобки. В данном случае применимо первое правило раскрытия скобок, а именно опускание скобок вместе с плюсом, который стоит перед этими скобками:
2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6
Пример 3. Раскрыть скобки в выражении 6+(−3)+(−2)
В обоих местах, где имеются скобки, перед ними стоит плюс. Здесь опять же применяется первое правило раскрытия скобок:
6 + (−3) + (−2) = 6 − 3 − 2
Иногда первое слагаемое в скобках записано без знака. Например, в выражении 1+(2+3−4) первое слагаемое в скобках 
На самом деле даже будучи в скобках перед двойкой стоит плюс, но мы его не видим по причине того, что его не записывают. Мы уже говорили, что полная запись положительных чисел выглядит как +1, +2, +3. Но плюсы по традиции не записывают, поэтому мы и видим привычные для нас положительные числа 1, 2, 3.
Поэтому, чтобы раскрыть скобки в выражении 1+(2+3−4), нужно как обычно опустить скобки вместе с плюсом, стоящим перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:
1 + (2 + 3 − 4) = 1 + 2 + 3 − 4
Пример 4. Раскрыть скобки в выражении −5 + (2 − 3)
Перед скобками стоит плюс, поэтому применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед этими скобками. Но первое слагаемое, которое в скобках записываем со знаком плюс:
−5 + (2 − 3) = −5 + 2 − 3
Пример 5. Раскрыть скобки в выражении (−5)
Перед скобками стоит плюс, но он не записан по причине того, что до него не было других чисел или выражений. Наша задача убрать скобки, применив первое правило раскрытия скобок, а именно опустить скобки вместе с этим плюсом (даже если он невидим)
Наша задача убрать скобки, применив первое правило раскрытия скобок, а именно опустить скобки вместе с этим плюсом (даже если он невидим)
(−5) = −5
Пример 6. Раскрыть скобки в выражении 2a + (−6a + b)
Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишется без изменений:
2a + (−6a + b) = 2a −6a + b
Пример 7. Раскрыть скобки в выражении 5a + (−7b + 6c) + 3a + (−2d)
В данном выражении имеется два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишется без изменений:
5a + (−7b + 6c) + 3a + (−2d) = 5a −7b + 6c + 3a − 2d
Второе правило раскрытия скобок
Теперь рассмотрим второе правило раскрытия скобок. Оно применяется тогда, когда перед скобками стоит минус.
Оно применяется тогда, когда перед скобками стоит минус.
Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный.
Например, раскроем скобки в следующем выражении
5 − (−2 − 3)
Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, стоящим перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:
Мы получили выражение без скобок 5 + 2 + 3. Данное выражение равно 10, как и предыдущее выражение со скобками было равно 10.
5 − (−2 − 3) = 10
5 + 2 + 3 = 10
Таким образом, между выражениями 5−(−2−3) и 5+2+3 можно поставить знак равенства, поскольку они равны одному и тому же значению:
5 − (−2 − 3) = 5 + 2 + 3
10 = 10
Пример 2. Раскрыть скобки в выражении 6 − (−2 − 5)
Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок, а именно опускаем скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, записываем с противоположными знаками:
При этом слагаемые, которые были в скобках, записываем с противоположными знаками:
6 − (−2 − 5) = 6 + 2 + 5
Пример 3. Раскрыть скобки в выражении 2 − (7 + 3)
Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:
2 − (7 + 3) = 2 − 7 − 3
Пример 4. Раскрыть скобки в выражении −(−3 + 4)
Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:
−(−3 + 4) = 3 − 4
Пример 5. Раскрыть скобки в выражении −(−8 − 2) + 16 + (−9 − 2)
Здесь два места, где нужно раскрыть скобки. В первом случае нужно применить второе правило раскрытия скобок, а когда очередь доходит до выражения +(−9 − 2) нужно применить первое правило:
−(−8 − 2) + 16 + (−9 − 2) = 8 + 2 + 16 − 9 − 2
Пример 6. Раскрыть скобки в выражении −(−a − 1)
Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:
−(−a − 1) = a + 1
Пример 7. Раскрыть скобки в выражении −(4a + 3)
Раскрыть скобки в выражении −(4a + 3)
Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:
−(4a + 3) = −4a − 3
Пример 8. Раскрыть скобки в выражении a − (4b + 3) + 15
Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:
a − (4b + 3) + 15 = a − 4b − 3 + 15
Пример 9. Раскрыть скобки в выражении 2a + (3b − b) − (3c + 5)
Здесь два места, где нужно раскрыть скобки. В первом случае нужно применить первое правило раскрытия скобок, а когда очередь доходит до выражения −(3c+5) нужно применить второе правило:
2a + (3b − b) − (3c + 5) = 2a + 3b − b − 3c − 5
Пример 10. Раскрыть скобки в выражении −a − (−4a) + (−6b) − (−8c + 15)
Здесь три места, где нужно раскрыть скобки. Вначале нужно применить второе правило раскрытия скобок, затем первое, а затем опять второе:
Вначале нужно применить второе правило раскрытия скобок, затем первое, а затем опять второе:
−a − (−4a) + (−6b) − (−8c + 15) = −a + 4a − 6b + 8c − 15
Механизм раскрытия скобок
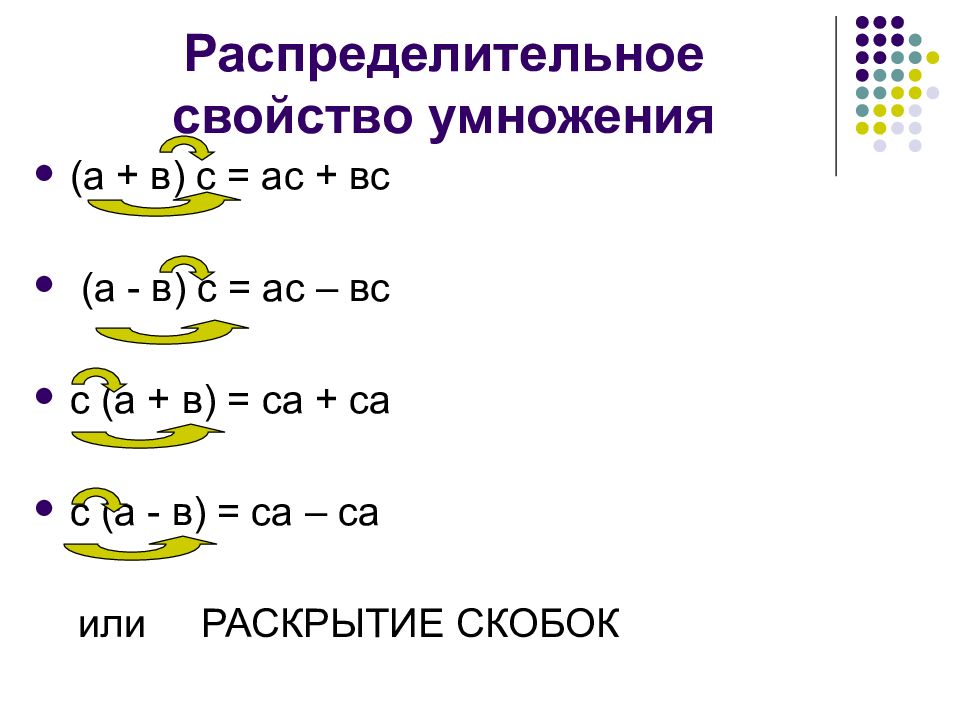
Правила раскрытия скобок, которые мы сейчас рассмотрели, основаны на распределительном законе умножения:
a(b + c) = ab + ac
На самом деле раскрытием скобок называют ту процедуру, когда общий множитель умножают на каждое слагаемое в скобках. В результате такого умножения скобки исчезают. Например, раскроем скобки в выражении 3×(4+5)
3 × (4 + 5) = 3 × 4 + 3 × 5
Поэтому, если нужно умножить число на выражение в скобках (или выражение в скобках умножить на число) надо говорить раскроем скобки.
Но как связан распределительный закон умножения с правилами раскрытия скобок, которые мы рассматривали ранее?
Дело в том, что перед любыми скобками стоит общий множитель. В примере 3 × (4 + 5) общий множитель это 3. А в примере a(b + c) общий множитель это переменная a.
А в примере a(b + c) общий множитель это переменная a.
Если перед скобками нет чисел или переменных, то общим множителем является 1 или −1, в зависимости от того, какой знак стоит перед скобками. Если перед скобками стоит плюс, значит общим множителем является 1. Если перед скобками стоит минус, значит общим множителем является −1.
К примеру, раскроем скобки в выражении −(3b − 1). Перед скобками стоит минус, поэтому нужно воспользоваться вторым правилом раскрытия скобок, то есть опустить скобки вместе с минусом, стоящим перед скобками. А выражение, которое было в скобках, записать с противоположными знаками:
−(3b − 1) = −3b + 1
Мы раскрыли скобки, воспользовавшись правилом раскрытия скобок. Но эти же скобки можно раскрыть, воспользовавшись распределительным законом умножения. Для этого сначала записываем перед скобками общий множитель 1, который не был записан:
−1(3b −1)
Минус, который раньше стоял перед скобками относился к этой единице. Теперь можно раскрыть скобки, применяя распределительный закон умножения. Для этого общий множитель −1 нужно умножить на каждое слагаемое в скобках и полученные результаты сложить.
Теперь можно раскрыть скобки, применяя распределительный закон умножения. Для этого общий множитель −1 нужно умножить на каждое слагаемое в скобках и полученные результаты сложить.
Для удобства заменим разность, находящуюся в скобках на сумму:
−1(3b −1) = −1( 3b + (−1) )
Далее умножаем общий множитель −1 на каждое слагаемое в скобках:
−1(3b −1) = −1(3b + (−1)) = −1 × 3b + (−1) × (−1) = −3b + 1
Как и в прошлый раз мы получили выражение −3b + 1. Каждый согласится с тем, что в этот раз затрачено больше времени на решение столь простейшего примера. Поэтому разумнее пользоваться готовыми правилами раскрытия скобок, которые мы рассматривали в данном уроке:
−(3b − 1) = −3b + 1
Но не мешает знать, как эти правила работают.
В данном уроке мы научились ещё одному тождественному преобразованию. Вместе с раскрытием скобок, вынесением общего за скобки и приведением подобных слагаемых можно немного расширить круг решаемых задач. Например:
Например:
Раскрыть скобки и привести подобные слагаемые в следующем выражении:
Здесь нужно выполнить два действия — сначала раскрыть скобки, а потом привести подобные слагаемые. Итак, по порядку:
1) Раскрываем скобки:
2) Приводим подобные слагаемые:
В получившемся выражении −10b+(−1) можно раскрыть скобки:
Пример 2. Раскрыть скобки и привести подобные слагаемые в следующем выражении:
1) Раскроем скобки:
2) Приведем подобные слагаемые. В этот раз для экономии времени и места, не будем записывать, как коэффициенты умножаются на общую буквенную часть
Пример 3. Упростить выражение 8m+3m и найти его значение при m=−4
1) Сначала упростим выражение. Чтобы упростить выражение 8m+3m, можно вынести в нём общий множитель m за скобки:
8m + 3m = m(8 + 3)
2) Находим значение выражения m(8 + 3) при m = −4. Для этого в выражение m(8 + 3) вместо переменной m подставляем число −4
Для этого в выражение m(8 + 3) вместо переменной m подставляем число −4
m (8 + 3) = −4 (8 + 3) = −4 × 8 + (−4) × 3 = −32 + (−12) = −44
Задания для самостоятельного решения
Задание 1. Раскройте скобки в следующем выражении:
Задание 2. Раскройте скобки в следующем выражении:
Задание 3. Раскройте скобки в следующем выражении:
Задание 4. Раскройте скобки в следующем выражении:
Задание 5. Раскройте скобки в следующем выражении:
Задание 6. Раскройте скобки в следующем выражении:
Задание 7. Раскройте скобки в следующем выражении:
Задание 8. Раскройте скобки в следующем выражении:
Задание 9. Раскройте скобки в следующем выражении:
Задание 10. Раскройте скобки в следующем выражении:
Задание 11. Раскройте скобки в следующем выражении:
Задание 12. Раскройте скобки в следующем выражении:
Задание 13. Раскройте скобки в следующем выражении:
Раскройте скобки в следующем выражении:
Задание 14. Раскройте скобки в следующем выражении:
Задание 15. Раскройте скобки в следующем выражении:
Задание 16. Раскройте скобки в следующем выражении:
Задание 17. Раскройте скобки в следующем выражении:
Задание 18. Раскройте скобки в следующем выражении:
Задание 19. Раскройте скобки в следующем выражении:
Задание 20. Раскройте скобки в следующем выражении:
Задание 21. Раскройте скобки в следующем выражении:
Задание 22. Раскройте скобки и приведите подобные слагаемые в следующем выражении:
Задание 23. Раскройте скобки и приведите подобные слагаемые в следующем выражении:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
правила и примеры (7 класс)
Основная функция скобок – менять порядок действий при вычислениях значений числовых выражений. Например, в числовом выражении \(5·3+7\) сначала будет вычисляться умножение, а потом сложение: \(5·3+7 =15+7=22\). А вот в выражении \(5·(3+7)\) сначала будет вычислено сложение в скобке, и лишь потом умножение: \(5·(3+7)=5·10=50\).
Например, в числовом выражении \(5·3+7\) сначала будет вычисляться умножение, а потом сложение: \(5·3+7 =15+7=22\). А вот в выражении \(5·(3+7)\) сначала будет вычислено сложение в скобке, и лишь потом умножение: \(5·(3+7)=5·10=50\).
Однако если мы имеем дело с алгебраическим выражением, содержащим переменную — например таким: \(2(x-3)\) – то вычислить значение в скобке не получается, мешает переменная. Поэтому в таком случае скобки «раскрывают», используя для этого соответствующие правила.
Правила раскрытия скобок
Если перед скобкой стоит знак плюс, то скобка просто снимается, выражение в ней при этом остается неизменным. Иначе говоря:
\((a-b)=a-b\)
Здесь нужно пояснить, что в математике для сокращения записей принято не писать знак плюс, если он стоит в выражении первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не \(+7+3\), а просто \(7+3\), несмотря на то, что семерка тоже положительное число. Аналогично если вы видите, например, выражение \((5+x)\) – знайте, что перед скобкой стоит плюс, который не пишут.
Аналогично если вы видите, например, выражение \((5+x)\) – знайте, что перед скобкой стоит плюс, который не пишут.
Пример. Раскройте скобку \((1+y-7x)\).
Решение: \((1+y-7x)=1+y-7x\).
Пример. Упростите выражение: \(3+(5-2x)\).
Решение: Раскрываем скобку согласно правилу, а затем приводим подобные слагаемые:
Пример. Раскройте скобку и приведите подобные слагаемые: \((x-11)+(2+3x)\).
Решение: \((x-11)+(2+3x)=x-11+2+3x=4x-9\).
Если перед скобкой стоит знак минус, то при снятии скобки каждый член выражения внутри нее меняет знак на противоположный:
\(-(a-b)=-a+b\)
Здесь нужно пояснить, что у \(a\), пока оно стояло в скобке, был знак плюс (просто его не писали), и после снятия скобки этот плюс поменялся на минус.
Пример: Упростите выражение \(2x-(-7+x)\).
Решение: внутри скобки два слагаемых: \(-7\) и \(x\), а перед скобкой минус. Значит, знаки поменяются – и семерка теперь будет с плюсом, а икс – с минусом. Раскрываем скобку и приводим подобные слагаемые.
Пример. Раскройте скобку: \(-(4m+3)\).
Решение: \(-(4m+3)=-4m-3\).
Пример. Раскройте скобку и приведите подобные слагаемые \(5-(3x+2)+(2+3x)\).
Решение: \(5-(3x+2)+(2+3x)=5-3x-2+2+3x=5\).
Если перед скобкой стоит множитель, то каждый член скобки умножается на него, то есть:
\(c(a-b)=ca-cb\)
Пример. Раскройте скобки \(5(3-x)\).
Решение: В скобке у нас стоят \(3\) и \(-x\), а перед скобкой — пятерка. Значит, каждый член скобки умножается на \(5\) — напоминаю, что знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.
Пример. Раскройте скобки \(-2(-3x+5)\).
Решение: Как и в предыдущем примере, стоящие в скобке \(-3x\) и \(5\) умножаются на \(-2\).
Пример. Упростить выражение: \(5(x+y)-2(x-y)\).
Решение: \(5(x+y)-2(x-y)=5x+5y-2x+2y=3x+7y\).
Осталось рассмотреть последнюю ситуацию.
При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй:
\((c+d)(a-b)=c·(a-b)+d·(a-b)=ca-cb+da-db\)
Пример. Раскройте скобки \((2-x)(3x-1)\).
Решение: У нас произведение скобок и его можно раскрыть сразу по формуле выше. Но чтобы не путаться, давайте сделаем всё по шагам.
Шаг 1. Убираем первую скобку — каждый ее член умножаем на скобку вторую:
Шаг 2. Раскрываем произведения скобки на множитель как описано выше:
— сначала первое…
— потом второе.
Шаг 3. Теперь перемножаем и приводим подобные слагаемые:
Так подробно расписывать все преобразования совсем необязательно, можно сразу перемножать. Но если вы только учитесь раскрывать скобок – пишите подробно, меньше будет шанс ошибиться.
Примечание ко всему разделу. На самом деле, вам нет необходимости запоминать все четыре правила, достаточно помнить только одно, вот это: \(c(a-b)=ca-cb\). Почему? Потому что если в него вместо c подставить единицу, получиться правило \((a-b)=a-b\). А если подставить минус единицу, получим правило \(-(a-b)=-a+b\). Ну, а если вместо c подставить другую скобку – можно получить последнее правило.
Скобка в скобке
Иногда в практике встречаются задачи со скобками, вложенными внутрь других скобок. Вот пример такого задания: упростить выражение \(7x+2(5-(3x+y))\).
Чтобы успешно решать подобные задания, нужно:
— внимательно разобраться во вложенности скобок – какая в какой находиться;
— раскрывать скобки последовательно, начиная, например, с самой внутренней.
При этом важно при раскрытии одной из скобок не трогать все остальное выражение, просто переписывая его как есть.
Давайте для примера разберем написанное выше задание.
Пример. Раскройте скобки и приведите подобные слагаемые \(7x+2(5-(3x+y))\).
Решение:
|
\(7x+2(5\)\(-(3x+y)\)\()=\) |
Выполнять задание начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относиться – это сама скобка и минус перед ней (выделено зеленым). Всё остальное (не выделенное) переписываем также как было. |
|
| \(=7x+2(5\)\(-3x-y\)\()=\) |
Теперь раскрываем вторую скобку, внешнюю. |
|
| \(=7x+2·5-2·3x-2·y=\) |
Упрощаем получившееся выражение… |
|
|
\(=7x+10-6x-2y=\) |
…и приводим подобные. |
|
|
\(=x+10-2y\) |
Готово. |
Пример. Раскройте скобки и приведите подобные слагаемые \(-(x+3(2x-1+(x-5)))\).
Решение:
|
\(-(x+3(2x-1\)\(+(x-5)\)\())\) |
Здесь тройная вложенность скобок. Начинаем с самой внутренней (выделено зеленым). Перед скобкой плюс, так что она просто снимается. |
|
|
\(-(x+3(2x-1\)\(+x-5\)\())\) |
Теперь нужно раскрыть вторую скобку, промежуточную. Но мы перед этим упростим выражение привидением подобный слагаемых в этой второй скобке. |
|
|
\(=-(x\)\(+3(3x-6)\)\()=\) |
Вот сейчас раскрываем вторую скобку (выделено голубым). Перед скобкой множитель – так что каждый член в скобке умножается на него. |
|
|
\(=-(x\)\(+9x-18\)\()=\) |
Вновь приводим подобные. |
|
|
\(=-(10x-18)=\) |
И раскрываем последнюю скобку. Перед скобкой минус – поэтому все знаки меняются на противоположные. |
|
|
\(=-10x+18\) |
Готово. |
Раскрытие скобок — это базовое умение в математике. Без этого умения невозможно иметь оценку выше тройки в 8 и 9 классе. Поэтому рекомендую хорошо разобраться в этой теме.
Без этого умения невозможно иметь оценку выше тройки в 8 и 9 классе. Поэтому рекомендую хорошо разобраться в этой теме.
Смотрите также:
Вынесение общего множителя за скобки
Entering Input | Mathematica & Wolfram Language for Math Students—Fast Intro
В документах Wolfram на локальном компьютере или в облаке, для начала работы нужно просто набрать нужное выражение и, затем, нажать SHIFT+ENTER для расчета:
| In[1]:= | X2 + 2 |
| Out[1]= |
Метки In[n] и Out[n] обозначают соответствующие входные и выходные данные. Символ % обозначает результат последних вычислений:
| In[1]:= | ⨯1 + 2 + 3 |
| Out[1]= |
| In[2]:= | ⨯% + 4 |
| Out[2]= |
После выполнения расчетов появляется Suggestions Bar, которая предлагает несколько вариантов последующих действий:
Для обозначения математических операций используются традиционные символы:
(Для умножения используйте пробел или *, а не символ “x”. (1 + 2))/4
(1 + 2))/4| Out[2]= |
Язык Wolfram содержит более 5 000 встроенных функций, покрывающих множество различных областей математики.
Аргументы встроенных функций разделяются между собой запятыми и заключены в квадратные скобки:
| In[1]:= | ⨯GCD[12, 15] |
| Out[1]= |
Если Вы не знаете, какую функцию использовать, просто наберите = в начале строки для активации естественной формы ввода:
| In[2]:= | Xplot a sine curve |
| Out[2]= |
Списки представляют собой коллекцию элементов и задаются с помощью фигурных скобок { . .. }:
.. }:
| In[1]:= | ⨯{1, 2, 3}
{x, y, z} |
Элементы в списках упорядочены. Они могут содержать цифры, переменные, результаты вычислений, а также другие списки.
Многие встроенные операторы к спискам применяются поэлементно:
| In[2]:= | ⨯{1, 2, 3} + 2 |
| Out[2]= |
Нумерация элементов списка начинается с 1. Части списка могут быть получены с помощью двойных квадратных скобок [[ … ]]:
| In[3]:= | ⨯{a, b, c, d}[[3]] |
| Out[3]= |
Создавать списки можно легко, благодаря таким функциям как Range:
| In[1]:= | ⨯Range[10] |
| Out[1]= |
Справочная информация: Управление вычислениями в документах »
Справочная информация: Ввод в свободной форме и внешние данные »
Справочная информация: Операции со списками »
Hands–on Start to
Wolfram Mathematica »
Полная документация »
Demonstrations Project »
Как раскрывать скобки в выражениях и уравнениях.
 Правила математики.
Правила математики.Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Этот прием носит название раскрытия скобок.
Раскрыть скобки означает избавить выражение от этих скобок.
Отдельного внимания заслуживает еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения
3−(5−7) мы получаем выражение 3−5+7. Оба этих выражения мы можем записать в виде равенства 3−(5−7)=3−5+7.
И еще один важный момент. В математике для сокращения записей принято не писать знак плюс, если он стоит в выражении или в скобках первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не +7+3, а просто 7+3, несмотря на то, что семерка тоже положительное число. Аналогично если вы видите, например, выражение (5+x) – знайте, что и перед скобкой стоит плюс, который не пишут, и перед пятеркой стоит плюс +(+5+x).
Аналогично если вы видите, например, выражение (5+x) – знайте, что и перед скобкой стоит плюс, который не пишут, и перед пятеркой стоит плюс +(+5+x).
Правило раскрытия скобок при сложении
При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.
Пример. Раскрыть скобки в выражении 2 + (7 + 3) Перед скобками плюс, значит знаки перед числами в скобках не меняем.
2 + (7 + 3) = 2 + 7 + 3
Правило раскрытия скобок при вычитании
Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный. Отсутствие знака перед первым слагаемым в скобках подразумевает знак +.
Пример. Раскрыть скобки в выражении 2 − (7 + 3)
Перед скобками стоит минус, значит нужно поменять знаки перед числами из скобок. В скобках перед цифрой 7 знака нет, это значит, что семерка положительная, считается, что перед ней знак +.
2 − (7 + 3) = 2 − (+ 7 + 3)
При раскрытии скобок убираем из примера минус, который был перед скобками, и сами скобки 2 − (+ 7 + 3) , а знаки, которые были в скобках, меняем на противоположные.
2 − (+ 7 + 3) = 2 − 7 − 3
Раскрытие скобок при умножении
Если перед скобками стоит знак умножения, то каждое число, стоящее внутри скобок, умножается на множитель, стоящий перед скобками. При этом умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.
Таким образом, сскобки в произведениях раскрываются в соответствии с распределительным свойством умножения.
Пример. 2 · (9 — 7) = 2 · 9 — 2 · 7
При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй скобки.
(2 + 3) · (4 + 5) = 2 · 4 + 2 · 5 + 3 · 4 + 3 · 5
На самом деле, нет необходимости запоминать все правила, достаточно помнить только одно, вот это: c(a−b)=ca−cb. Почему? Потому что если в него вместо c подставить единицу, получится правило (a−b)=a−b. А если подставить минус единицу, получим правило −(a−b)=−a+b. Ну, а если вместо c подставить другую скобку – можно получить последнее правило.
Почему? Потому что если в него вместо c подставить единицу, получится правило (a−b)=a−b. А если подставить минус единицу, получим правило −(a−b)=−a+b. Ну, а если вместо c подставить другую скобку – можно получить последнее правило.
Раскрываем скобки при делении
Если после скобок стоит знак деления, то каждое число, стоящее внутри скобок, делится на делитель, стоящий после скобок, и наоборот.
Пример. (9 + 6) : 3=9 : 3 + 6 : 3
Как раскрыть вложенные скобки
Если в выражении присутствуют вложенные скобки, то их раскрывают по порядку, начиная с внешних или внутренних.
При этом важно при раскрытии одной из скобок не трогать остальные скобки, просто переписывая их как есть.
Пример. 12 — (a + (6 — b) — 3) = 12 — a — (6 — b) + 3 = 12 — a — 6 + b + 3 = 9 — a + b
Как найти Область Допустимых Значений (ОДЗ)
Допустимые и недопустимые значения переменных
В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.
Первым делом школьники изучают выражения с переменными.
Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.
Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.
Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.
Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.
Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.
Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.
Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.
Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.
Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.
В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.
Пример 1
Рассмотрим выражение
В выражении три переменные (a, b, c).
Запишем значения переменных в виде: a = 1, b = 1, c = 2.
Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:
Таким же образом можем выяснить, какие значения переменных — недопустимые.
a = 1, b = 2, c = 1.
Подставим значения переменных в выражение
На ноль делить нельзя.
Что такое ОДЗ
ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».
Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.
Запоминаем!
ОДЗ относится к выражениям. Область определения функции относится к функциям и не относится к выражениям.
Пример 2
Рассмотрим выражение
ОДЗ такого выражения выглядит следующим образом: ( — ∞; 3) ∪ (3; +∞).
Читать запись нужно вот так:
Область допустимых значений переменной x для выражения — это числовое множество ( — ∞; 3) ∪ (3; +∞).
Пример 3
Рассмотрим выражение
ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.
Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.
Как найти ОДЗ: примеры решения
Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.
Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.
Мы не можем вычислить значение выражения, если:
- требуется извлечение квадратного корня из отрицательного числа
- присутствует деление на ноль (математическое правило номер раз: никогда не делите на ноль)
- отрицательный целый показатель в степени при отрицательном числе
- требуется вычисление логарифма отрицательного числа
- область определения тангенса = π * k, где k ∈ z
- область определения котангенса π * k, где k ∈ z
- нахождение арксинуса и арккосинуса числа, выходящего за пределы числового промежутка [- 1, 1].
Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.
Давайте потренируемся находить ОДЗ.
Пример 4
Найдем область допустимых значений переменной выражения a3 + 4 * a * b − 6.
Как решаем:
В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a3 + 4 * a * b − 6 при любых значениях переменной.
ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.
Ответ: (a и b), где a — любое число и b — любое число.
Пример 5
Найдем область допустимых значений (ОДЗ) переменной выражения
Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.
Это значит, что мы может сказать, что ОДЗ переменной a в выражении — пустое множество.
Пустое множество изображается в виде вот такого символа Ø.
Пример 6
Найдем область допустимых значений (ОДЗ) переменных в выражении
Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.
Лайфхак
Чтобы не потратить зря время на решение нерешаемого примера, всегда обращайтесь к списку условий, при которых выражение не может быть решено.
Пример 7
Найдем ОДЗ переменной a в выражении
Прежде всего, нам нужно подобрать такое условие, при котором в знаменателе дроби не будет ноля —
Мы знаем, что выражение под знаком корня должно быть положительным. Это дает нам второе условие: a + 1 ≥ 0.
Мы не можем вычислить логарифм отрицательного выражения. Получаем третье условие: a2 + 2 > 0.
Выражении в основании логарифма не должно быть отрицательным и не должно равняться единице. Получаем условие 4: a + 6 > 0.
Условие 5: a + 6 ≠ 1.
Определим ОДЗ, опираясь на все означенные условия:
a +1 — 1 0.
Ответ: ОДЗ: [ — 1; 0) ∪ (0; +∞)
Как видите, записывая ОДЗ, мы ставим квадратные и круглые скобки.
Запомните
- Если число входит в ОДЗ, то около числа ставим квадратные скобки.
- Если число не входит в ОДЗ, то около него ставятся круглые скобки.
Например, если х > 6, но х < 8, то записываем интервал [6; 8).
Зачем учитывать ОДЗ при преобразовании выражения
Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.
Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.
В этом может помочь определение ОДЗ.
Тождественное преобразование может:
- расширить ОДЗ
- никак не повлиять на ОДЗ
- сузить ОДЗ
Рассмотрим каждый случай в отдельности.
Пример 8
Рассмотрим выражение a + 4/a — 4/a
Поскольку мы должны следить за тем, чтобы в выражении не возникало деление ноль, определяем условие a ≠ 0.
Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).
В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.
ОДЗ для a — это R — множество всех вещественных чисел.
Преобразование расширило ОДЗ — добавился ноль.
Пример 9
Рассмотрим выражение a2 + a + 4 * a
ОДЗ a для этого выражения — множество R.
В выражении есть подобные слагаемые, выполним тождественное преобразование.
После приведения подобных слагаемых выражение приняло вид a2 + 5 * a
ОДЗ переменной a для этого выражения — множество R.
Это значит, что тождественное преобразование никак не повлияло на ОДЗ.
Пример 10
Рассмотрим выражение
ОДЗ a определяется неравенством (a — 1) * (a — 4) ≥ 0.
Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).
Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.
Приведем выражение к виду
ОДЗ переменной a для этого выражения определяется неравенствами:
a — 1 ≥ 0
a — 4 ≥ 0
Решив систему линейных неравенств, получаем множество [4; + ∞).
Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).
Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.
Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.
Тебе следует повторить тему — формулы сокращенного умножения!
скобок по математике: типы и примеры — видео и стенограмма урока
Скобки и группировка
Часто можно встретить математические скобки, используемые для группировки . Эти скобки могут включать:
Эти скобки могут включать:
При использовании для группировки скобки всегда идут парами. Будет открывающаяся скобка и закрывающая скобка .
Скобки используются для ясности порядка операций. — порядка, в котором несколько операций должны выполняться в математическом выражении.
Например, предположим, что у вас есть следующее выражение: 2 + 4 * 6 — 1. Несмотря на то, что вы могли прочитать на Facebook, есть только один правильный ответ на это выражение. Вы выполняете умножение и деление, двигаясь слева направо, прежде чем выполнять сложение и вычитание, также перемещаясь слева направо. Произведя сначала умножение, вы получите 2 + 24 — 1 = 25.
Что, если вместо этого вы захотите сначала выполнить сложение и вычитание (а затем умножить результаты)? Используйте скобки.Теперь проблема принимает следующий вид: (2 + 4) * (6 — 1) = 6 * 5 = 30. В этом примере круглые скобки говорят вам сделать что-то отличное от обычного порядка операций. В других случаях они просто используются для визуальной ясности.
Несколько уровней группировки
Возможно, вы захотите выполнить группировку внутри группировки. Если это так, то такие выражения сбивают с толку: 2 + (1 + (3 + 2 * (4 + 5))). Хотя нет ничего плохого в использовании нескольких уровней круглых скобок (а иногда в компьютерных приложениях у вас нет выбора), на это немного сложно смотреть.
Вместо этого вы можете использовать разные типы скобок для каждого уровня. В математике чаще всего используются круглые скобки для первого уровня (первая операция, которую вы должны выполнить), квадратные скобки для следующего уровня и фигурные скобки для последнего уровня: 2 + {1 + [3 + 2 * (4 + 5)]}.
В любом случае, вы сначала выполняете внутреннюю группировку (4 + 5), а оттуда двигаетесь наружу, как показано ниже:
2 + {1 + [3 + 2 * 9]} = 2 + {1 + [3 + 18 ]} = 2 + {1 + 21} = 2 + 22 = 24 Это немного похоже на поиск выхода из особняка вашего дяди Джерома.Сначала вам нужно выбраться из гостевой комнаты, затем вы выберетесь с третьего этажа, а затем вы выберетесь из самого дома. Сначала вы начинаете с самой внутренней «загадки», а оттуда двигаетесь наружу.
Сначала вы начинаете с самой внутренней «загадки», а оттуда двигаетесь наружу.
Другое использование скобок
Однако иногда скобки используются не для группирования. Например, если вы работаете с функциями , тогда f ( x ) означает «функция f с x в качестве входных данных». В этом случае круглые скобки используются для обозначения аргументов или входных данных функции.
Также круглые скобки могут использоваться для обозначения упорядоченной пары , например (3, -1). Вы часто будете видеть, что это используется для обозначения декартовых координат : если вы наносите точку на оси x и y , то (3, -1) будет конкретной точкой на декартовой плоскости, где x равно 3 и y равно -1.
Или скобки могут представлять обозначение интервала . (1,5) может означать все значения от чуть более одного до почти пяти.[4,6] может означать все числа от четырех до шести, включая четыре и шесть.
Фигурные скобки также часто используются для обозначения множеств. Например, {3, 4, 5, 6} означает набор, включающий числа 3, 4, 5 и 6. Угловые скобки, такие как <1,3>, могут указывать на внутренний продукт в продвинутой математике или физике. class, а квадратные скобки могут означать, что то, что находится внутри, является матрицей.
Итак, как узнать, что означают скобки, если их можно использовать по-разному? Точно так же вы узнаете, относится ли «синий» к цвету глаз вашего любимого человека или к ощущению, которое вы испытываете, когда он бросает вас ради лучшего друга — по контексту.
Краткое содержание урока
Математические скобки часто используются для группировки, чтобы указать порядок, в котором должен выполняться набор математических операций. Однако в некоторых случаях скобки используются для специальных математических целей.
Ключевые точки
- Группировка : скобки будут включать: (), [] & {}
- Открывающая скоба и закрывающая скоба : все скобки попарно
- Порядок операций : порядок, в котором несколько операций должны выполняться в математическом выражении
- Функции : в скобках используется f ( x ), что означает «функция f с x в качестве входных данных»
- Аргументы : круглые скобки используются для указания входных данных функции
- Упорядоченная пара : круглые скобки могут использоваться для обозначения пар, например (3, -1)
- Декартовы координаты : нанесение точки на оси x и y —
- Интервальное обозначение : (1,5) может означать все значения от чуть более одного до почти пяти
- Внутренний продукт : угловые скобки, такие как <1,3>; может указывать наборы в продвинутом классе математики или физики
Результаты обучения
Просматривая урок по использованию скобок, сделайте своей целью:
- Иллюстрировать математические скобки
- Приведите примеры различных применений скоб.

- Выделите их использование для нескольких уровней группировки
- Обсудите роль скобок в сообщении аргументов и указании упорядоченных пар, а также в представлении обозначений интервалов и наборов.
Что такое круглые скобки? — MVOrganizing
Что такое круглые скобки?
Круглые скобки (также называемые круглыми скобками, особенно в американском английском) в основном используются для отделения информации, которая не важна для значения остальной части предложения.Если вы удалите заключенный в скобки материал, предложение все равно будет иметь смысл.
Следует использовать квадратные или круглые скобки?
Круглые скобки — это знаки препинания, которые используются для выделения информации в тексте или абзаце. Вне смайликов круглые скобки всегда идут парами. Скобки, иногда называемые квадратными скобками, чаще всего используются, чтобы показать, что слова были добавлены к прямой цитате.
Что такое грамматические скобки?
Скобки (круглые скобки) — это знаки препинания, используемые в предложении для включения информации, которая не является существенной для основной мысли. Информация в скобках обычно является дополнительной; если бы оно было удалено, смысл предложения остался бы неизменным.
Информация в скобках обычно является дополнительной; если бы оно было удалено, смысл предложения остался бы неизменным.
Где вы ставите скобки в сумме?
Кронштейны. Индексы. Деление и умножение (начните слева и отработайте их в том порядке, в котором вы их найдете) Сложение и вычитание (когда в сумме осталось только сложение и вычитание, обработайте их в том порядке, в котором вы их найдете — начиная с левой стороны от суммы). сумму и двигаясь вправо)
Что означают прямые скобки в математике?
Самый распространенный способ представления абсолютного значения числа или выражения — окружить его символом абсолютного значения: двумя вертикальными прямыми линиями.| 6 | = 6 означает, что «абсолютное значение 6 равно 6.» | –6 | = 6 означает, что «абсолютное значение –6 равно 6.» | –2 — x | означает «абсолютное значение выражения –2 минус x».
Что означают 3 вертикальные линии в математике?
В математике тройная черта иногда используется как символ идентичности или отношения эквивалентности (хотя и не единственная; другие распространенные варианты включают ~ и ≈). В частности, в геометрии он может использоваться либо для того, чтобы показать, что две фигуры совпадают, либо что они идентичны.
В частности, в геометрии он может использоваться либо для того, чтобы показать, что две фигуры совпадают, либо что они идентичны.
Что означают фигурные скобки в математике?
Символы фигурных скобок (также называемые фигурными скобками). Фигурные скобки чаще всего используются как (1) символы группировки в математическом выражении и (2) символы группировки, используемые для идентификации набора элементов. При использовании в математическом выражении левая фигурная скобка «{» и правая фигурная скобка «}» используются вместе.
Где фигурные скобки клавиатуры?
Фигурные скобки, которые также называются открытой скобкой, закрывающей скобкой и волнистыми скобками, находятся на тех же клавишах, что и открытая скобка [и закрывающая скобка] на клавиатурах США.
Что означают фигурные скобки в наборах?
Фигурные скобки {} обозначают набор. Итак, у вас есть два набора, один {x} и другой {{x}}, давайте обозначим первый набор как A = {x}, затем второй набор будет {A}, и ваше утверждение будет ли A∈ {A} или нет. , что, конечно, верно.
, что, конечно, верно.
Что означает двойная скобка?
Ответ и объяснение: Двойные скобки или [[]] в математике относятся к округлению внутреннего значения до его наибольшего целого числа, меньшего или равного значению.
Скобки — это то же самое, что круглые скобки в математике?
Круглые скобки — это гладкие и изогнутые (), квадратные скобки [] и фигурные {}.В математике они в основном используются для определения порядка операций. Скобки также используются для представления массивов, а фигурные скобки используются в наборах и последовательностях.
| Набор текста форматирование | Только текст форматирование | Банкноты | |
| (2, 3) | (2, 3) | В скобках укажите баллы. Квадратные скобки и другие обозначения (или вообще ничего) имеют другое значение. Квадратные скобки и другие обозначения (или вообще ничего) имеют другое значение. | |
| (2, 3) | (2, 3) | Когда вы пишете открытый интервал, используйте круглые скобки и обратите внимание, что «это интервал», чтобы отличать интервал от точки. | |
| [2, 3] | [2, 3] | Используйте квадратные скобки для обозначения закрытых интервалов. | |
| [2, ∞) | [2, бесконечность) [2, бесконечность) | Для «бесконечности» либо произнесите слово по буквам, либо сократите до «inf.». Не пытайтесь аппроксимировать символ бесконечности двумя строчными буквами О. Кстати, никогда не используйте квадратную скобку на бесконечности. «Бесконечность» — это не число, поэтому вы не можете «включить» его в интервал. | |
| A ∪ B | A-соединение-B A U B | Если вы не указали объединение множеств (как в первой строке слева), то определите вашу нотацию.B | Если вы не указали пересечение множества, определите свои обозначения, чтобы читатель не ошибся, что карат указывает на показатель степени. |
| A ⊂ B | A-подмножество-B A Если вы не разъясняете отношение подмножества, определите, что вы подразумеваете под символом «меньше». | | |
| A ⊆ B | A-подмножество или аналогичное-B A <= B | Если вы не разъясняете отношение подмножества, определите вашу нотацию «меньше или равно».c | Либо сформулируйте отношение дополнения, либо определите «до степени c» как «набор дополнений». |
| А — В | A-дополнение-B A — B | Вы можете описать отношение дополнения, если хотите, но почти все понимают обозначение «минус». | |
| a ∈ A | a находится в A a-элементе-A | Символ «является элементом» — непростой.Не пытайтесь приблизить его с помощью заглавной буквы E; даже несмотря на то, что «все» пытаются его использовать, читателей это почти всегда сбивает с толку. (Можно подумать, что мы научимся, но … нет.) Просто объясните отношения. | |
| a ∉ A | a не входит в A a не является элементом A | Объясните отношение. | |
| ∅ | {} пустой набор Ø | Фигурные скобки обычно используются для обозначения наборов, поэтому вы можете использовать фигурные скобки без каких-либо элементов между ними для обозначения пустого набора. Или (на ПК), удерживая нажатой клавишу «ALT», введите «0216» на цифровой клавиатуре. Или (на ПК), удерживая нажатой клавишу «ALT», введите «0216» на цифровой клавиатуре. | |
| {1, 2, 3} | {1, 2, 3} | Наборы обычно записываются с помощью фигурных скобок. Не используйте круглые скобки или другие символы группировки или, что еще хуже, вообще не используйте символы группировки. | |
| N {1, 2, 3 ,…} натуральные числа | Если вы используете букву «N» для обозначения «набора натуральных чисел», скажите читателю, что вы имеете в виду. | ||
| Z {…, -1, 0, 1, 2, …} целые числа | Если вы используете букву «Z» для обозначения «набора целых чисел», скажите читателю, что вы имеете в виду. В противном случае укажите набор, который вы имеете в виду. | ||
| R вещественные числа | Если вы используете только букву «R» для «набора всех действительных чисел», определите обозначение. В противном случае укажите набор, который вы имеете в виду. | ||
| Q рациональные | Если вы используете только букву «Q» для «набора всех рациональных чисел» (то есть набора всех дробей), определите обозначение.В противном случае укажите набор, который вы имеете в виду. | ||
| C комплексные числа | Если вы используете «C» для «набора всех комплексных чисел», определите обозначение. В противном случае укажите набор, который вы имеете в виду. | ||
| ⇒ | . если (это), то (то) ==> | Либо укажите отношение «если-то», либо приблизьте стрелку, используя два знака «равно», чтобы отличить «если-то» от «больше или равно». | |
| ⇔ | iff тогда и только тогда, когда <==> | Сокращение «iff» для «если и только если» является довольно стандартным и должно быть распознано в контексте, но если вы не уверены, разъясните его. | |
| ∃ | существует (а) | Не пытайтесь подделать этот символ. и | В контексте логического утверждения, карат следует распознать как значение «и», но поясните, если вы не уверены. |
| ∨ | v или | Использование «v» вместо символа «или» может сбивать с толку, поэтому либо объясните, что вы имеете в виду, либо четко определите, что вы имеете в виду под «v». | |
| ˜ ¬ | ~ ! не | Существуют различные символы для «не», поэтому определите свое обозначение, независимо от того, что вы используете.На практике часто проще всего использовать «не — (что угодно)». |
Разница между скобками и круглыми скобками
Ключевое отличие: Скобки и круглые скобки — это символы, используемые для заключения слов или чисел. Скобки обычно относятся к квадратным или квадратным скобкам с символом [], тогда как круглые или круглые скобки обозначаются символом (). Оба по-разному используются в математике и обычном английском.Скобки — это в основном символы, которые используются парами для обозначения группы, состоящей из различных членов.Существуют различные типы кронштейнов, например —
Круглые или круглые скобки с символом ()
Квадратные или квадратные скобки с символом []
Скобки или фигурные скобки с символом {}
Кронштейны угловые <>
Однако, как правило, квадратные скобки используются для обозначения квадратных скобок. В математике он используется для обозначения интервалов, используемых для выражения области и диапазона функций. Скобка (одинарная) используется, если точка не входит в интервал, а скобка используется, когда точка включена.
В математике он используется для обозначения интервалов, используемых для выражения области и диапазона функций. Скобка (одинарная) используется, если точка не входит в интервал, а скобка используется, когда точка включена.
Например — (5, 6] — это означает, что 5 исключено, а 6 включено в этот интервал.
Интервал для бесконечности или отрицательной бесконечности всегда обозначается круглыми скобками, это связано с тем, что бесконечность не может содержаться, и поэтому выражается с помощью круглых скобок вместо скобок. Также можно использовать обратные скобки для обозначения скобок.
Круглые скобки обычно используются в математике для группировки выражений, которые используются для определения порядка приоритета в операциях.Квадратные скобки в математике обычно используются для заключения аргументов функций.
В обычном письменном языке также широко используются круглые скобки, особенно для разделения второстепенного материала. Например — машина (украденная Джо) была красного цвета. В этом предложении можно просто пропустить материал, украденный Джо, поскольку он не влияет и не изменяет значение в окружающем предложении. Он также используется, когда нет уверенности в вопросах, связанных с полом, предметом единственного или множественного числа и т. Д.С другой стороны, квадратные скобки чаще всего используются для изменения цитируемого текста кем-то, кто не является первоначальным автором.
В этом предложении можно просто пропустить материал, украденный Джо, поскольку он не влияет и не изменяет значение в окружающем предложении. Он также используется, когда нет уверенности в вопросах, связанных с полом, предметом единственного или множественного числа и т. Д.С другой стороны, квадратные скобки чаще всего используются для изменения цитируемого текста кем-то, кто не является первоначальным автором.
Нравится — «Она [Лили] была рада видеть его [Джеймса]»
Это может быть сделано для добавления пропущенных слов, добавления некоторого редакционного комментария и т. Д. Можно также использовать скобки для включения материала в скобках в материал в скобках, например — Он был председателем (очень высокая должность [оплачивалась] в течение длительного времени).
Сравнение скобок и круглых скобок:
Кронштейны | Скобки | |
Символ | [] | () |
Интервальное обозначение | Используется для изображения этой точки. | Используется для обозначенной точки не входит |
Общий курс математики | Для включения аргументов функций Ложь функции Range, Sin и т. Д. | Для группировки выражений и определения приоритета операций |
На простом английском | За изменение цитируемого текста кем-то, кто не является первоначальным автором. | Специально для отделения второстепенных материалов |
Использование на английском языке | Сравнительно реже | Более общий |
Кронштейн — GIS Wiki | Энциклопедия ГИС
Скобки — это знаки препинания, используемые парами для выделения или вставки текста в другой текст.В Соединенных Штатах «скобка» иногда относится конкретно к квадратному или прямоугольному типу. [1]
Существует четыре основных типа скоб:
- круглые скобки , открытые скобки или круглые скобки : ()
- квадратные скобки , закрытые скобки или квадратные скобки : []
- фигурных скобок , волнистых скобок , закрученных скобок , скобок или куриных губ : {}
- угловые скобы , ромбовидные скобы , конические скобы или шевроны : <> или ⟨
История
Угловая скобка была первым шрифтом, появившимся на английском языке. Дезидериус Эразм ввел термин лунула для обозначения закругленных скобок (), напоминающих круглую форму луны. [2]
Дезидериус Эразм ввел термин лунула для обозначения закругленных скобок (), напоминающих круглую форму луны. [2]
Использование
Помимо обозначения класса скобок всех типов, неквалифицированное слово скобка чаще всего используется для обозначения определенного типа скобок. В современном американском использовании это обычно квадратная скобка, тогда как в современном британском использовании это обычно скобка (круглая скобка).
В американском обиходе круглые скобки обычно рассматриваются отдельно от других скобок, и называть их «скобками» вообще необычно, даже если они выполняют аналогичную функцию. В более формальном использовании «круглые скобки» могут относиться ко всему тексту в квадратных скобках, а не только к используемым знакам препинания (так что весь текст в этом наборе круглых скобок можно назвать круглыми скобками).
Типы
Круглые скобки ()
Круглые скобки (единственное число, скобки ) — иногда называемые круглых скобок , изогнутых скобок , овальных скобок или просто скобок , или, в просторечии, скобок без скобок — содержат материал, который может быть опущен. уничтожение или изменение значения предложения.
уничтожение или изменение значения предложения.
Круглые скобки могут использоваться в официальном письме для добавления дополнительной информации, например «Sen. Эдвард Кеннеди (Д., Массачусетс) выступил подробно ». Они также могут обозначать сокращенное обозначение «единственного или множественного числа» для существительных — например, «притязания».
Фразы в скобках широко использовались в неформальной письменной форме и в литературе, посвященной сознанию. Особо следует отметить южноамериканского писателя Уильяма Фолкнера (см. Абсалом, Авессалом! и раздел Квентина Звуки и ярость ), а также поэт Э.Э. Каммингс. В большинстве текстов чрезмерное использование круглых скобок обычно является признаком плохо структурированного текста. Более мягкий эффект может быть получен при использовании пары запятых в качестве разделителя. Если предложение содержит запятые для других целей, это может привести к визуальной путанице.
Круглые скобки исторически использовались там, где в настоящее время используется тире, то есть для обозначения альтернатив, таких как «круглые скобки» (круглые скобки). Примеры такого использования можно увидеть в редакциях Fowler’s .
Примеры такого использования можно увидеть в редакциях Fowler’s .
Круглые скобки также могут быть вложенными (один набор (например, этот) внутри другого набора).Это обычно не используется в формальном письме (хотя иногда другие скобки [особенно квадратные скобки] будут использоваться для одной или нескольких внутренних скобок [другими словами, вторичных {или даже третичных } фраз можно найти внутри основное предложение]). [необходима ссылка ]
Любая пунктуация в круглых или других скобках не зависит от остального текста: «Mrs. Пеннифартинг (Что? Да, так ее звали!) Была моей квартирной хозяйкой.«В этом использовании пояснительный текст в круглых скобках заключен в круглые скобки. (Чаще всего заключенный в скобки текст находится в одном предложении, но также часто бывает, что все предложение или даже несколько предложений дополнительного материала заключаются в круглые скобки.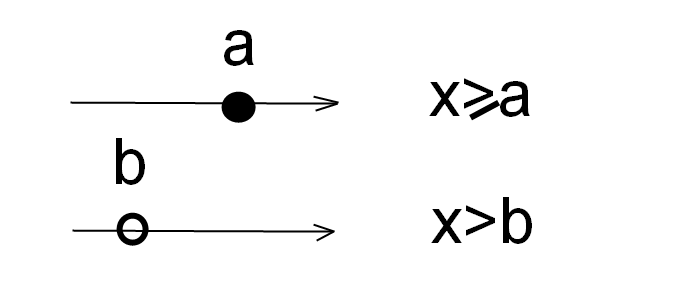 В этом случае даже последняя точка будет в скобках. Опять же, круглые скобки подразумевают, что смысл и последовательность текста в целом не изменились бы, если бы предложения в скобках были удалены.)
В этом случае даже последняя точка будет в скобках. Опять же, круглые скобки подразумевают, что смысл и последовательность текста в целом не изменились бы, если бы предложения в скобках были удалены.)
Круглые скобки в математике означают различный приоритет операторов.Например, 2 + 3 × 4 будет 14, поскольку умножение выполняется до сложения. С другой стороны, (2 + 3) × 4 равно 20, потому что круглые скобки имеют приоритет над обычным приоритетом, в результате чего добавление выполняется первым. Они также используются для разделения аргументов в математических функциях. Например, f (x) — это функция f , применяемая к переменной x. Круглые скобки обозначают набор координат в системе координат. (4,7), например, может представлять точку, расположенную в 4 на оси x и 7 на оси y.Круглые скобки также могут обозначать интервалы. (0,5), например, представляет собой интервал между 0 и 5, не включая 0 или 5. Круглые скобки также могут представлять умножение, как в случае 2 (3) = 6.![]() Некоторые авторы следуют соглашению в математических уравнениях, что , когда круглые скобки имеют один уровень вложенности, внутренняя пара — это круглые скобки, а внешняя пара — квадратные скобки. Пример:
Некоторые авторы следуют соглашению в математических уравнениях, что , когда круглые скобки имеют один уровень вложенности, внутренняя пара — это круглые скобки, а внешняя пара — квадратные скобки. Пример:
Круглые скобки также могут использоваться для представления биномиального коэффициента.
Круглые скобки используются в компьютерном программировании, особенно в языке программирования C и подобных языках, для передачи параметров или аргументов функциям или методам, например, в следующем примере:
В декартовой системе координат скобки используются для указания координат точки: (2,3) обозначает точку с координатой x 2 и координатой y 3.
Рамные или квадратные скобки []
Квадратные скобки в основном используются для заключения пояснительных или отсутствующих материалов, обычно добавляемых кем-то, кроме исходного автора, особенно в цитируемом тексте. [3] Примеры включают: «Я ценю это [честь], но я должен отказаться» и «будущее псионики [см. Определение] под вопросом» .
Определение] под вопросом» .
Выражение в квадратных скобках [sic] используется для обозначения ошибок, которые «таким образом находятся в оригинале»; многоточие в квадратных скобках […] часто используется для обозначения удаленного материала; комментарии в квадратных скобках указывают на то, что исходный текст был изменен для ясности: «Я хотел бы поблагодарить [несколько неважных людей] и моих родителей [ sic ] за их любовь, терпимость […] и помощь [курсив мой]». [4]
Квадратные скобки используются в математике в различных обозначениях, включая стандартные обозначения для интервалов, коммутаторов, скобок Ли и скобок Айверсона.
В переведенных произведениях квадратные скобки используются для обозначения того же слова или фразы на языке оригинала, чтобы избежать двусмысленности. [5] Например: Он обучен открытой ладони [карате].
Когда необходимы вложенные круглые скобки, квадратные скобки могут использоваться вместо внутренней пары круглых скобок во внешней паре. [6] Когда необходимы более глубокие уровни вложенности, обычно принято чередовать круглые и квадратные скобки на каждом уровне или использовать фигурные скобки. [необходима ссылка ]
[6] Когда необходимы более глубокие уровни вложенности, обычно принято чередовать круглые и квадратные скобки на каждом уровне или использовать фигурные скобки. [необходима ссылка ]
Фонетическая транскрипция может быть заключена в квадратные скобки [7] , часто с использованием международного фонетического алфавита.Обратите внимание, что фонематическая, а не фонетическая транскрипция обычно использует парные косые черты, а не скобки.
Квадратные скобки также могут использоваться в химии для обозначения концентрации химического вещества или комплексного иона.
Квадратные скобки могут использоваться в компьютерном программировании для доступа к элементам массива, особенно в C-подобных языках. Они используются в руководствах по программированию для обозначения отсутствующих или дополнительных параметров.
Квадратные скобки (называемые символов перемещения влево или символов перемещения вправо ) добавляются по бокам текста при корректуре, чтобы указать изменения в отступах:
| Сдвинуть влево | [К Судьбе я подаю в суд, лишенный других средств, единственное убежище для оставшихся несчастных. |
|---|---|
| Центр | ] Потерянный рай [ |
| Двигаться вверх |
Квадратные скобки используются для обозначения частей текста, которые необходимо проверить при подготовке черновиков перед окончательной доработкой документа. Они часто обозначают моменты, которые еще не согласованы в законопроектах, и год, в котором был составлен отчет по определенным решениям прецедентного права.
HTML-объекты в квадратных скобках: & # 91; и & # 93;
Сверху: квадратные скобки, фигурные скобки (фигурные скобки), круглые скобки, угловые скобки и (красным) знаки неравенства.Фигурные скобки или фигурные скобки {}
Фигурные скобки (также называемые фигурными скобками или «волнистыми скобками») иногда используются в прозе для обозначения серии равных вариантов: «Выберите свое животное (козу, овцу, корову, лошадь} и следуйте за мной».Они используются особым образом в поэзии и музыке (для обозначения повторов или соединенных строк). Музыкальные термины для этого знака, соединяющего нотоносцы, — это награда и «скобка», и они соединяют две или более музыкальных строк, которые воспроизводятся одновременно. [8] В математике разграничивают множества. Во многих языках программирования они заключают в себя группы операторов. Поэтому такие языки (C — один из самых известных примеров) называются языками фигурных скобок. Некоторые люди используют фигурную скобку для обозначения движения в определенном направлении.
Музыкальные термины для этого знака, соединяющего нотоносцы, — это награда и «скобка», и они соединяют две или более музыкальных строк, которые воспроизводятся одновременно. [8] В математике разграничивают множества. Во многих языках программирования они заключают в себя группы операторов. Поэтому такие языки (C — один из самых известных примеров) называются языками фигурных скобок. Некоторые люди используют фигурную скобку для обозначения движения в определенном направлении.
Предположительно из-за сходства слов скобка и скобка (хотя у них нет общей этимологии), многие люди небрежно рассматривают скобка как синоним скобка . Поэтому, когда необходимо избежать любой возможности путаницы, например, в компьютерном программировании, может быть лучше использовать термин фигурная скобка , а не скобка . Однако в общем употреблении в североамериканском английском предпочтение отдается последней форме. [необходима ссылка ] Термин фигурные скобки является избыточным, поскольку других типов скобок не существует. Индийские программисты часто используют название «цветочная скобка». [9]
Индийские программисты часто используют название «цветочная скобка». [9]
Фигурные скобки часто используются в интернет-сообществах и в обмене мгновенными сообщениями для обозначения объятий. [10]
Угловые скобки, ромбовидные скобки или шевроны 〈〉
Угловые скобки (〈〉 [11] ; Unicode U + 27E8 и U + 27E9; и другие, см. Ниже) часто используются для заключения выделенного материала.Некоторые словари используют угловые скобки, чтобы заключить короткие отрывки, иллюстрирующие использование слов.
В физических науках угловые скобки используются для обозначения среднего во времени или другого непрерывного параметра. Например,
Внутреннее произведение двух векторов обычно записывается как, но также используются обозначения (a, b).
В лингвистике угловые скобки обозначают орфографию, например: «Английское слово / kæt / пишется как 〈cat〉».
В текстовой критике и, следовательно, во многих изданиях плохо переданных произведений угловые скобки обозначают разделы текста, которые нечитаемы или иным образом утеряны; редактор часто вставляет в них свою собственную реконструкцию.
Угловые скобки нечасто используются для обозначения диалога, который мыслится, а не произносится, например:
- 〈Какой красивый цветок!〉
Одинарные и двойные угловые скобки или пары операторов сравнения (<<, >>) (то есть намного меньше и намного больше ) иногда используются вместо нитей ( «,») (Используется как кавычки на многих языках), когда соответствующие глифы недоступны.
Математические или логические символы для «больше» (>) и «меньше» (<) являются операторами неравенства и не являются знаками препинания при их использовании.Тем не менее, поскольку настоящие угловые скобки недоступны на типичной компьютерной клавиатуре, вместо них часто используются символы «меньше» и «больше». Когда они используются таким образом, их часто вольно называют угловыми кронштейнами . Например, символы <и> часто используются для разделения URL-адресов в тексте, например «Я нашел это на Example.com.
 Также часто можно встретить указание адреса электронной почты, например: «Авторские права на эту фотографию принадлежат John Smith
Также часто можно встретить указание адреса электронной почты, например: «Авторские права на эту фотографию принадлежат John Smith
Шевроны являются частью стандартной китайской и корейской знаков препинания, где они обычно заключают названия книг: ︿ и ﹀ или ︽ и ︾ для традиционной вертикальной печати и 〈и〉 или 《и》 для горизонтальной печати.
В комиксах угловые скобки часто используются для обозначения диалогов, которые условно переведены с другого языка; Другими словами, если персонаж говорит на другом языке, вместо того, чтобы писать на другом языке и предоставлять перевод, он записывает переведенный текст в угловые скобки.Конечно, поскольку на самом деле ни один иностранный язык не написан, это всего переведено условно . [необходима ссылка ]
[необходима ссылка ]
Угловые скобки также могут использоваться для обозначения действия или статуса (например, <Волны> или <Не в сети>), особенно в онлайн-обсуждениях в режиме реального времени (обмен мгновенными сообщениями, бюллетень). доски и т. д.). (Здесь звездочки также могут использоваться для обозначения действия.)
Вычислительная техника
Кодировка
- Открывающая и закрывающая круглых скобок соответствуют символам ASCII и Unicode 40 и 41 или U + 0028 и U + 0029, соответственно.
- Для квадратных скобок соответствующие значения — 91 и 93 или U + 005B и U + 005D.
- Для скоб , 123 и 125 или U + 007B и U + 007D. Скобки впервые стали частью набора символов с 8-битным кодом IBM 7030 Stretch [12] .
- Истинные угловые скобки доступны в Unicode в кодовых точках U + 27E8 и U + 27E9 (для математического использования) и / или U + 3008 и U + 3009 (для языков Восточной Азии).
 Третий набор угловых скобок закодирован в U + 2329 и U + 232A, но официально «не рекомендуется для математического использования» [13] , потому что они канонически эквивалентны кодовым точкам CJK U + 300x и, следовательно, могут отображаться как двойные -ширинные символы.Символы меньше и больше часто используются в качестве замены угловых скобок. Они находятся как в Unicode, так и в ASCII в кодовых точках 60 и 62 или U + 003C и U + 003E.
Третий набор угловых скобок закодирован в U + 2329 и U + 232A, но официально «не рекомендуется для математического использования» [13] , потому что они канонически эквивалентны кодовым точкам CJK U + 300x и, следовательно, могут отображаться как двойные -ширинные символы.Символы меньше и больше часто используются в качестве замены угловых скобок. Они находятся как в Unicode, так и в ASCII в кодовых точках 60 и 62 или U + 003C и U + 003E.
Эти различные символы скобок часто используются во многих компьютерных языках в качестве операторов или для другой синтаксической разметки. Далее следуют наиболее распространенные варианты использования.
Использование «(» и «)»
- часто используются для определения синтаксической структуры выражений, отменяя приоритет операторов:
a * (b + c)имеет подвыраженияaиb + c, тогда какa * b + cимеет подвыраженияa * bиc - содержат параметры или аргументы функций или могут обозначать вызов функции или подобной функции конструкции:
substring ($ val, 10,1) - в Лиспе, они открывают и закрывают s-выражения и, следовательно, работают с приложениями:
(cons a b) - в языках семейства Fortran, они также используются для ссылок на массивы От
- на языке программирования Perl до Perl 5, они используются для определения списков , статических структур, подобных массиву; эта идиома распространяется на их использование в качестве контейнеров аргументов подпрограммы (функции)
- на языке программирования Perl 6, они определяют захватов , структуру, которая откладывает контекстную интерпретацию.
 Это использование распространяется и на обычные круглые скобки. Они также используются для указания аргументов для вызовов функций и для объявления сигнатур формальных параметров или других переменных.
Это использование распространяется и на обычные круглые скобки. Они также используются для указания аргументов для вызовов функций и для объявления сигнатур формальных параметров или других переменных. - в Python они используются для устранения неоднозначности литералов кортежей (неизменяемых упорядоченных списков), которые обычно формируются запятыми в тех местах, где круглые скобки и запятые в противном случае были бы частью вызова функции.
- в Tcl они используются для включения имени элемента переменной ассоциативного массива
- используется для создания улыбки или хмурого лица в чате в мгновенных сообщениях или текстовых сообщениях (см. Смайлик).
Использование «[» и «]»
- относятся к элементам массива или ассоциативного массива, а иногда и для определения количества элементов в массиве:
queue [3] - может использоваться для определения буквального анонимного массива или списка:
[5, 10, 15] - в большинстве синтаксисов регулярных выражений квадратные скобки обозначают класс символов: набор возможных символов на выбор из
- в Tcl, они включают в себя суб-скрипт, который нужно оценить, и результат будет заменен на
- в химии, [c] обозначает концентрацию определенного вещества — в этом примере c.

- в некоторых языках Microsoft .NET (CLI), в первую очередь C # и C ++, они используются для обозначения атрибутов метаданных.
- используется для создания смайлов в текстовых сообщениях или мгновенных сообщениях
- x86 Внедрение сборки, такое как FASM, они используются, чтобы отличать указатели от их данных
Использование «{» и «}»
- используются в некоторых языках программирования для определения начала и конца блоков кода или данных. Говорят, что языки, использующие это соглашение, принадлежат к семейству языков программирования с фигурными скобками .
- используются для представления определенных определений типов или буквальных значений данных, таких как составная структура или ассоциативный массив
- в математике они заключают в себя элементы набора и обозначают набор
- в Curl они используются для разграничения выражений и операторов (аналогично тому, как в Lisp используются круглые скобки).
- в Паскале определяют начало и конец комментариев
- в большинстве синтаксисов регулярных выражений, они используются как квантификаторы, соответствующие n повторений предыдущей группы
- в Perl они также используются для обозначения элементов ассоциативного массива
- в PHP они используются для определения структур.
- в Tcl они заключают строку, которая должна быть заменена без выполнения каких-либо внутренних замен
- на сленге IRC, две фигурные скобки, одна из которых закрывающая, обозначают поцелуй:} {
- в Python они используются для словарей
- в LaTeX они группируют части, имеющие один и тот же локальный формат, или параметры переноса
Использование «
<» и «>»В вычислениях символы «меньше» и «больше» иногда используются с функцией, подобной скобкам.Когда эти символы используются парами, как если бы они были скобками,
- в SGML (и его приложениях и вариантах, таких как HTML и XML), используется для включения тегов кода:
- в C ++, C # и Java они разграничивают общие аргументы
- при написании текста, содержащего адреса электронной почты или URI, они отделяют каноническую часть адреса от любого окружающего текстового содержимого, особенно когда в противном случае могут возникнуть двусмысленность.
- в Perl через Perl 5 они используются для чтения строки из источника ввода
- в Perl 6 они сочетают цитирование и поиск по ассоциативному массиву
- в ABAP они обозначают символы полей — заполнители или символические имена для других полей, которые могут указывать на любой объект данных.
- используется для мысленного общения
Когда не используется парами для разграничения текста (не используется в качестве скобок),
- знаки «меньше» и «больше» (возможно, в сочетании с другими знаками препинания) являются общими операторами отношения; в некоторых языках пара вместе как
<>обозначает сравнение неравенства - при дублировании как
<<или>>они могут представлять операторы битового сдвига или в C ++ также как операторы потокового ввода / вывода - - это операторы для указания перенаправления ввода / вывода в различных командных оболочках.В этом контексте их часто называют hoinkies (единственное число hoinky ), чтобы «избежать путаницы с другими операторами скобочного типа». [14]
Стили макета
Основная статья: Стиль отступаВ обычном письме (прозе) открывающая скобка редко остается висящей в конце строки текста, а закрывающая скобка не может ее начинать. Однако в компьютерном коде это часто делается специально для облегчения чтения. Например, список элементов в квадратных скобках, разделенных точкой с запятой, может быть записан в квадратных скобках в отдельных строках, а элементы, за которыми следует точка с запятой, - каждый в одной строке.
Распространенная ошибка программирования - несовпадение фигурных скобок; соответственно, во многих IDE есть фигурные скобки для выделения совпадающих пар.
Математика
Основная статья: Кронштейн (математика)В дополнение к использованию круглых скобок для указания порядка операций, круглые и квадратные скобки используются для обозначения интервала. Обозначение
[a, c) используется для обозначения интервала от a до c , который включает a , но не включает c .То есть,
[5, 12) будет набором всех действительных чисел от 5 до 12, включая 5, но не 12. Числа могут быть сколь угодно близки к 12, включая 11,999 и так далее (с любым конечным числом 9. ), но 12.0 не входит. В Европе обозначение
[5,12 [также используется для этого. Конечная точка, примыкающая к квадратной скобке, известна как закрытая , а конечная точка, примыкающая к скобке, известна как открытая . Если оба типа скобок одинаковы, весь интервал может обозначаться как закрытый или открытый соответственно.Когда в качестве конечной точки используется бесконечность или отрицательная бесконечность, она обычно считается открытой и добавляется в круглые скобки. См. «Интервал» (математика) для более полного описания.
В квантовой механике угловые скобки также используются как часть формализма Дирака, обозначения скобок, для обозначения векторов из двойных пространств Бра ( ) и Кета ( | B> ). Математики также обычно пишут < a , b > для внутреннего произведения двух векторов.В статистической механике угловые скобки обозначают ансамбль или среднее значение по времени. Угловые скобки используются в теории групп для записи групповых представлений и для обозначения подгруппы, порожденной набором элементов.
В теории групп и теории колец квадратные скобки обозначают коммутатор. В теории групп коммутатор
[ г , ч
] обычно определяется как г -1 ч -1 гч . В теории колец коммутатор
[ a , b
] определяется как ab - ba .Кроме того, в теории колец скобки обозначают коммутатор, где { a , b } определяется как ab + ba . Квадратная скобка также используется для обозначения производной Ли или, в более общем смысле, скобки Ли в любой алгебре Ли.
Различные обозначения, такие как винкулум, действуют аналогично скобкам при указании порядка операций или ином группировании нескольких символов для общей цели.
В формальном языке спецификации Z фигурные скобки определяют набор, а угловые скобки определяют последовательность.
Бухгалтерский учет
Традиционно в бухгалтерском учете отрицательные суммы заключаются в скобки. [15]
Закон
Квадратные скобки используются при цитировании юридических отчетов для выявления параллельных ссылок на неофициальных репортеров. Например: Хроника Паб. Co. против Верховного суда, (1998) 54 Cal.2d 548, [7 Cal.Rptr. 109].
Если цитируемый материал каким-либо образом изменен, изменения заключаются в скобки внутри цитаты. Например: Истец утверждает, что его причина является справедливой, заявляя: «[m] y причин является [ sic ] справедливым.В то время как в исходном процитированном предложении слово «мой» было написано с заглавной буквы, оно было изменено в цитате, и это изменение обозначено скобками. Точно так же, когда цитата содержала грамматическую ошибку, цитирующий автор сигнализировал, что ошибка была в оригинале, с помощью «[ sic ]» (латинское означает «таким образом»). ( California Style Manual , раздел 4:59 (4-е изд.))
Спорт
Турнирные скобки, схематическое представление серии игр, сыгранных во время турнира, обычно приводящих к одному победителю, названы так из-за их сходства с квадратными или фигурными скобками.
Набор текста
В ролевой игре и письме скобки используются для предложений, не связанных с речью (также известных как OOC, несимволы). Пример:
(как вас зовут?)
Также в ролевой игре иногда предпочитают использовать двойные круглые скобки для OOC, а иногда и квадратные скобки, в зависимости от личных предпочтений. [необходима ссылка ]
См. Также
- Смайлик
- Японские типографские символы
Список литературы
- ↑ Бесплатный онлайн-словарь по вычислительной технике
- ↑ Трасс, Линн. Eats, Shoots & Leaves , 2003. стр. 161. ISBN 1-592-40087-6.
- ↑ Чикагское руководство по стилю, 15-е изд. , Издательство Чикагского университета, 2003 г., §6.104
- ↑ The Columbia Guide to Standard American English (Колумбийский справочник по стандартному американскому английскому)
- ↑ Чикагское руководство по стилю, 15-е изд. , Издательство Чикагского университета, 2003 г., §6.105
- ↑ Чикагское руководство по стилю, 15-е изд. , Издательство Чикагского университета, 2003 г., §6.102 и §6.106
- ↑ Чикагское руководство по стилю, 15-е изд., Издательство Чикагского университета, 2003 г., §6.107
- ↑ decodeunicode.org> U + 007B LEFT CURLY BRACKET Проверено 3 мая 2009 г.
- ↑ К. Р. Венугопал, Раджкумар Буйя, Т. Равишанкар. Освоение C ++ , 1999. стр. 34. ISBN 0-07-463454-2.
- ↑ Смайлики Messenger См. Левое и правое объятия
- ↑ Некоторые шрифты неправильно отображают эти символы. Вместо этого обратитесь к изображению справа.
- ↑ Боб, Бемер, The Great Curly Brace Trace Chase , http: // www.bobbemer.com/BRACES.HTM, получено 5 сентября 2009 г.
- ↑ http://www.unicode.org/charts/PDF/U2300.pdf
- ↑ Bryant, Randal E .; О’Халларон, Дэвид. Компьютерные системы: взгляд программиста , 2003. стр. 794. ISBN 0-13-034074-X.
- ↑ Информационный центр IBM Information Management Software для z / OS Solutions
Библиография
- Леннард, Джон (1991). Но я отвлекся: использование круглых скобок в английском печатном стихе .Оксфорд: Clarendon Press. ISBN 0-19-811247-5.
- Тернбулл; и другие. (1964). Графика общения . Нью-Йорк: Холт. Утверждает, что то, что изображено выше в виде квадратных скобок, называется фигурными скобками, а фигурные скобки - скобками. Это была терминология в американской печати до компьютеров.
Типы, использование, правило BODMAS, решенные проблемы и ответы на часто задаваемые вопросы
Первый вопрос, который задает учащийся в этой теме, - «Как мы можем определить скобки».
При оценке выражения, содержащего подвыражение в квадратных скобках, квадратные скобки обозначают тип группировки, операторы в подвыражении имеют приоритет над окружающими его операторами. Кроме того, для различных скобок существует множество вариантов использования и определений.
Типы скоб
Часто используемые типы скоб:
Круглые скобки ()
Квадратные скобки []
Фигурные скобки {}
Угловые скобки ⟨9013
90Среди четырех различных типов скобок скобки являются наиболее часто используемым типом скобок.
В математических задачах круглые скобки в основном используются для группировки чисел. Используйте порядок операций для решения проблемы, когда мы видим несколько чисел и операций в круглых скобках.
В математике скобки используются для трех основных целей:
Для разделения чисел для пояснения.
Для обозначения умножения.
Для группировки номеров.
Чтобы разделить числа для пояснения, можно использовать круглые скобки.Например, если у нас есть дополнительная проблема с отрицательным числом, чтобы различать два знака, будут использоваться круглые скобки. Чтобы отличить число от его степени, также можно использовать круглые скобки. Обычно это происходит, если мы поднимаем отрицательное число для контроля.
Для чего нужны кронштейны?
Скобки, особенно скобки Скобки () используются в элементарной алгебре для определения порядка операций. В соответствии с правилом BODMAS, слова в скобках оцениваются первыми.
Пример: 5 * (2 + 4) - 30, (5 * 3) + 2 - 30.
Скобки часто используются в математических выражениях в целом для обозначения группировки, где это необходимо, для предотвращения двусмысленности и повышения ясности .
В декартовой системе координат скобки используются для обозначения координат точки.
Пример: (4,8) обозначает точки в системе координат x-y, где координата x равна 4, а координата y - 8.
Пример: f (x), g (x).
Пример: [0,8) обозначает полузакрытый интервал, который включает все действительные числа, кроме 8 от 0 до 8.
Широкие скобки вокруг двух чисел обозначают биномиальный коэффициент, один над другим.
Как и в (a, b, c), круглые скобки вокруг набора из двух или более чисел обозначают набор из n чисел, которые связаны определенным образом.
Матрица обозначается широкими скобками вокруг массива чисел.
Для обозначения наибольшего общего делителя используются круглые скобки.
Правило BODMAS
Скобки находят свое основное применение в правиле BODMAS или PEMDAS, где последовательность операций, выполняемых при разрешении выражения. BODMAS или PEMDAS означает:
B - скобки, P - круглые скобки
O - порядок, E - экспоненты
D - деление
M - умножение
A - добавление
S - вычитание
BODMAS объясняет последовательность операций, которые необходимо выполнить, пока выражение не будет разрешено.Согласно закону BODMAS, если в выражении есть скобки ((), {}, []), мы сначала должны преодолеть или упростить скобку, за которой следует порядок, затем делить, умножать, складывать и вычитать слева направо. . В неправильном порядке решение проблемы приведет к неправильному ответу.
Основные проблемы со скобками и их применение:
1) Решите (2 + 4) - (6 - 3)
Ответ: В данном выражении заключены две круглые скобки. Мы можем решить оба из них по отдельности по правилу BODMAS, а затем объединить их результаты.
(2 + 4) = 6 ………. (1)
(6-3) = 3 ……… .. (2)
Теперь вычитая (1) с (2), получаем
( 2 + 4) - (6 - 3) = 6 - 3 = 3
2) Решить (3 + (5 * 4)) - ((4 * 6) - 10)
Ответ: Четыре скобки заключаются в данное выражение. Мы решим ее, используя правило BODMAS, чтобы найти ответ.
Первые скобки: (5 * 4) = 20 …………………………… .. (1)
Вторые скобки: (3 + (5 * 4)) = (3 + 20) = 23 ……… (2)
Третьи скобки: (4 * 6) = 24 …………………………… (3)
Четвертые скобки: ((4 * 6) - 10) = (24 - 10) = 14 …… (4)
Теперь вычтем (2) и (4) и получим
(3 + (5 * 4)) - ((4 * 6) - 10) = 23-14 = 9.
Почему некоторые слова заключены в квадратные скобки? - Цвета-NewYork.com
Почему некоторые слова заключены в квадратные скобки?
Скобки, иногда называемые квадратными скобками, чаще всего используются, чтобы показать, что слова были добавлены к прямой цитате. Иногда при цитировании человека или документа необходимо добавить пару слов, чтобы обеспечить достаточный контекст, чтобы цитата имела смысл.
Для чего нужны скобки в цитате?
Скобки: в документе используйте квадратные скобки для обозначения важной информации, добавляемой в прямые цитаты.Скобки говорят читателю, что информация добавлена для дальнейшего пояснения цитаты.
Что означает буква в скобках?
Скобки означают, что письмо редактировал писатель. Обычно это цитата, и автор, который цитирует, должен был изменить букву, чтобы цитата соответствовала - скажем, с верхнего регистра на нижний или наоборот - в его или ее собственный абзац.
Что означают скобки в юридической письменной форме?
Используйте пару скобок в цитате, чтобы заключить редакторский комментарий, исправление, объяснение, интерполяцию, замену или перевод, которых не было в исходном тексте.Используйте пару скобок вокруг любого символа, который вы изменяете или добавляете в цитируемый материал.
Как называются скобки?
Четыре основных парных символа пунктуации: скобка (или квадратная скобка; также называется скобкой в британском английском), скобка (множественное число: круглые скобки), фигурная скобка (фигурная скобка в британском английском) и знак неравенства (остроконечная скобка).
Почему юристы заключают числа в скобки?
Garner's Modern American Usage сообщает, что изначально это было сделано в юридической письменной форме, чтобы предотвратить мошеннические изменения.Вот почему вы иногда видите цифру в скобках после выписанного числа - это пережиток юридической письменности, но это не то, что вам нужно включать в свое письмо сегодня.
Когда следует заключать числа в круглые скобки?
Лучшее правило - записывать числа от одного до десяти, использовать цифры для чисел больше 10 и забыть о повторяющихся числах в скобках.
Какие числа в скобках?
Числа в круглых скобках - число, указанное в финансовой отчетности, заключенное в круглые скобки, является отрицательным числом.Если скобок нет, число положительное. Отчет о доходах и расходах - этот отчет показывает ежемесячный доход и понесенные расходы.
Почему в скобках указаны отрицательные числа?
(Вы, возможно, слышали выражение «залито красными чернилами» для компании, которая теряет деньги). Но у них не всегда есть цветные принтеры, поэтому они должны ставить знак минус перед отрицательными числами. Тем не менее, знак минус очень маленький, поэтому они согласились, для ясности, использовать вместо него скобки (или круглые скобки).
Какое правило для скобок в математике?
Для ясности можно использовать скобки для разделения чисел. Например, если у вас возникла проблема сложения с отрицательным числом, скобки будут использоваться для разделения двух знаков. Круглые скобки также могут использоваться для отделения числа от его степени. Обычно это происходит, если вы возводите отрицательное число в степень.
Что такое круглые скобки и примеры?
Используйте круглые скобки, чтобы заключить поясняющую информацию или использовать ее в качестве отступления.Пример: он наконец ответил (после пяти минут размышлений), что он не понял вопроса. Если материал в круглых скобках завершает предложение, точка ставится после скобок. Пример: он дал мне приятный бонус (500 долларов).
Как называется ()?
() называются круглыми скобками или круглыми скобками, {} называются фигурными скобками или скобками, а [] - квадратными скобками. Все они выполняют одну и ту же функцию, за исключением того, что имеют разные формы. Мы используем эти скобки, когда хотим заключить часть выражения в скобки.
Для чего нужны круглые скобки?
Круглые скобки () используются для заключения в предложение несущественной или дополнительной информации. Круглые скобки всегда используются парами; у вас должны быть открывающая и закрывающая круглые скобки. В формальном академическом письме рекомендуется экономно использовать круглые скобки.
В чем разница между круглыми и круглыми скобками?
Круглые скобки, конечно же, греческие и фактически означают «вставка». Он принял значение знаков "(" или ")".Скобки - правильное множественное число. Обычно вы используете пару знаков, обозначающих вставку, затем «в круглых скобках» - или скобки; тем не менее, «в скобках» означает: в последнюю очередь.
Что стоит в первых скобках?
В математике они в основном используются для определения порядка операций. Сначала вычисляются самые внутренние круглые скобки, за ними следуют скобки, которые образуют следующий слой наружу, а затем скобки, которые образуют третий слой наружу.
Как называются причудливые скобки?
У них {} множество имен; они называются фигурными скобками, фигурными скобками или волнистыми скобками.
Что означают одни круглые скобки?
: одна из пары знаков (), используемых для заключения слова или группы слов или для группировки математических терминов, рассматриваемых как единое целое. Другие слова в скобках.
Что значит)))?
Смысл))) простая улыбка, как эмодзи.
Что означают двойные скобки в текстовых сообщениях?
Двойные скобки указывают на то, что это интерполяция не докладчика, а репортера.
Можно ли использовать двойные скобки?
Отделяйте цитаты от текста в скобках точкой с запятой (для цитат в скобках) или запятыми вокруг года (для повествовательных цитат).Не используйте двойное закрытие или скобки, стоящие подряд.
Что такое вложенные круглые скобки?
Как и матрешки, некоторые арифметические выражения содержат наборы вложенных скобок - один набор скобок внутри другого набора. Эти разные стили помогают отслеживать, где начинается и где заканчивается утверждение в круглых скобках.
Что означают две точки и скобка?
две точки и правая скобка - это смайлик (сбоку) точка с запятой, а правая скобка - подмигивающий смайлик (сбоку) :-p - это смайлик, высунувший язык.
Как называются две точки?
Двоеточие: знак препинания, состоящий из двух точек одинакового размера, размещенных одна над другой на одной вертикальной линии. Двоеточие часто предшествует объяснению, списку или введению цитируемого предложения.
Что означают две точки?
многоточие
Что означает татуировка 3%?
Треугольная татуировка с тремя точками обычно обозначает понятие «mi vida loca», что по-испански означает «моя сумасшедшая жизнь», и обычно ассоциируется с сообществом банд и длительными сроками тюремного заключения.Хорошая новость в том, что это значение применимо только тогда, когда точки расположены треугольником.
Что означают 3 точки в текстовых сообщениях?
.





 Третий набор угловых скобок закодирован в U + 2329 и U + 232A, но официально «не рекомендуется для математического использования» [13] , потому что они канонически эквивалентны кодовым точкам CJK U + 300x и, следовательно, могут отображаться как двойные -ширинные символы.Символы меньше и больше часто используются в качестве замены угловых скобок. Они находятся как в Unicode, так и в ASCII в кодовых точках 60 и 62 или U + 003C и U + 003E.
Третий набор угловых скобок закодирован в U + 2329 и U + 232A, но официально «не рекомендуется для математического использования» [13] , потому что они канонически эквивалентны кодовым точкам CJK U + 300x и, следовательно, могут отображаться как двойные -ширинные символы.Символы меньше и больше часто используются в качестве замены угловых скобок. Они находятся как в Unicode, так и в ASCII в кодовых точках 60 и 62 или U + 003C и U + 003E.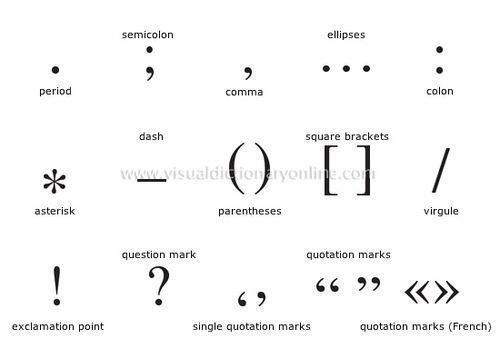 Это использование распространяется и на обычные круглые скобки. Они также используются для указания аргументов для вызовов функций и для объявления сигнатур формальных параметров или других переменных.
Это использование распространяется и на обычные круглые скобки. Они также используются для указания аргументов для вызовов функций и для объявления сигнатур формальных параметров или других переменных.