ОГЭ по информатике: Логические операции

Пример 1.

Для какого из приведённых чисел ложно высказывание: 

НЕ(число > 50) ИЛИ (число чётное)?
1) 9    2) 56     3) 123     4) 8

Решение. Сначала выполняем сравнения в скобках, затем операция НЕ, в последнюю очередь — операция ИЛИ.

1) Подставим число 9 в выражение:
НЕ (9 > 50) ИЛИ (9 чётное)
НЕ (ложь) ИЛИ (ложь) = истина ИЛИ ложь = истина

9 нам не подходит, так как по условию мы должны получить ложь.

2) Подставим число 56 в выражение:
НЕ (56 > 50) ИЛИ (56 чётное)
НЕ (истина) ИЛИ (истина) = ложь ИЛИ истина = истина

56 тоже не подходит.

3) Подставим 123:
НЕ (123 > 50) ИЛИ (123 чётное)
НЕ (истина) ИЛИ (ложь) = ложь 

ИЛИ ложь = ложь 

Число 123 подошло.

Эту задачу можно было решить и по-другому:
НЕ(число > 50) ИЛИ (число чётное)

Нам надо получить ложное значение. Мы видим, что операция ИЛИ будет выполняться в последнюю очередь. Операция ИЛИ даст ложь, когда оба выражения НЕ(число) и (число чётное) будут ложны.

Так как условие (число чётное) должно быть равно ложному значению, то сразу отвергаем варианты с числами 56, 8.

Далее, условие НЕ (число > 50) = ложь, соответственно условие (число > 50) = истина. Из двух оставшихся чисел 9 и 123 этому условию подходит число 123. 

Итак, можно решать прямой подстановкой, что долго и может дать ошибку при вычислении выражения; или же можно решать задачу быстро, проанализировав все простые условия.

Ответ: 3)

 

Пример 2

Для какого из приведённых чисел истинно высказывание:

НЕ(Первая цифра чётная) И НЕ(Последняя цифра нечётная)?

1) 6843       2)  4562       3) 3561       4) 1234

Сначала выполняем сравнения в скобках, затем операции НЕ над скобками, в последнюю очередь — операция И. Все это выражение должно принимать истинное значение.

Так как операция НЕ меняет смысл высказывания на противоположный, мы может переписать это сложное выражение так:

(Первая цифра нечётная)

И (Последняя цифра чётная) = истина 

Как известно, логическое умножение И дает истину только тогда, когда истинны все простые высказывания. Таким образом, оба условия должны быть истинными:

(Первая цифра нечётная) = истина       (Последняя цифра чётная) = истина

Как видно, подходит только число 1234

Ответ: 4)  

 

Пример 3

Для какого из приведённых имён истинно высказывание:
НЕ(Первая буква гласная) И (Количество букв > 5)?

1) Иван      2) Николай      3) Семён      4) Илларион

Перепишем выражение:
(Первая буква не гласная) И

 (Количество букв > 5) = истина 
(Первая буква согласная)  И (Количество букв > 5) = истина 

Оба условия должны выполняться (команда И дает истину когда оба входящих простых условия истинны).

Подходит имя «Николай» (первая буква не гласная и число букв 7>5).

Ответ: 2)

 

Пример 4

Для какого из приведённых значений числа X истинно высказывание:
НЕ (X > 5) И (X > 4)?

1) 4     2) 5     3) 6     4) 7

Первой выполняется операция НЕ, второй — И.

Перепишем выражение: (X ≤ 5) И (X > 4) = истина

Оба условия должны быть верными. Подходит число 5

Ответ: 2)

ОГЭ по информатике

Логические операции — урок. Информатика, 8 класс.

Сложные (составные) высказывания строятся из простых с помощью логических операций. Рассмотрим основные логические операции, определённые над высказываниями. Все они соответствуют связкам, употребляемым в естественном языке.

 

Название логической операции	Логическая связка
Инверсия	«не»; «неверно, что»
Конъюнкция	«и»; «а»; «но»; «хотя»
Дизъюнкция	«или»

Конъюнкция

Рассмотрим два высказывания:

\(A\) = «Основоположником алгебры логики является Джордж Буль»,

\(B\) = «Исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике».

Очевидно, новое высказывание «Основоположником алгебры логики является Джордж Буль, и исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике» истинно только в том случае, когда одновременно истинны оба исходных высказывания.

Конъюнкция — логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Для записи конъюнкции используются следующие знаки: И,ˆ,⋅,&.

Например: A И B,AˆB,A⋅B,A&B.

Конъюнкцию можно описать в виде таблицы, которую называют таблицей истинности:

 

В таблице истинности перечисляются все возможные значения исходных высказываний (столбцы \(A\) и \(B\)), причём соответствующие им двоичные числа, как правило, располагают в порядке возрастания: \(00, 01, 10, 11\). В последнем столбце записан результат выполнения логической операции для соответствующих операндов.

 

Обрати внимание!

Конъюнкцию также называют логическим умножением.

Дизъюнкция

Рассмотрим два высказывания:

\(A\) = «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу»,

\(B\) = «Лейбниц является основоположником бинарной арифметики».

Очевидно, новое высказывание «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания.

Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.

Для записи дизъюнкции используются следующие знаки: ИЛИ;∨;|;+.

Например: A ИЛИ B;A∨B;A|B;A+B.

Дизъюнкция определяется следующей таблицей истинности:

 

Обрати внимание!

Дизъюнкцию также называют логическим сложением.

Инверсия

Инверсия — логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.

Для записи инверсии используются следующие знаки: НЕ;¬;−

Например: НЕ А;¬А;А−.
Инверсия определяется следующей таблицей истинности:

 

 

Обрати внимание!

Инверсию также называют логическим отрицанием.

Отрицанием высказывания «У меня дома есть компьютер» будет высказывание «Неверно, что у меня дома есть компьютер» или, что в русском языке то же самое, что «У меня дома нет компьютера».

Отрицанием высказывания «Я не знаю китайский язык» будет высказывание «Неверно, что я не знаю китайский язык» или, что в русском языке: «Я знаю китайский язык».

Отрицанием высказывания «Все юноши \(8-х\) классов — отличники» является высказывание «Неверно, что все юноши \(8-х\) классов — отличники», другими словами, «Не все юноши \(8-х\) классов — отличники».

Таким образом, при построении отрицания к простому высказыванию либо используется речевой оборот «неверно, что …», либо отрицание строится к сказуемому, тогда к соответствующему глаголу добавляется частица «не».

 

Любое сложное высказывание можно записать и виде логического выражения — выражения, содержащего логические переменные, знаки логических операций и скобки.

 

Логические операции в логическом выражении выполняются в следующей очерёдности: инверсия, конъюнкция, дизъюнкция.

 

Изменить порядок выполнения операций можно с помощью расстановки скобок.

 

Обрати внимание!

Логические операции при выполнении имеют следующий приоритет: инверсия, конъюнкция, дизъюнкция.

Источники:

Босова Л. Л., Босова А. Ю., Информатика: учебник для 8 класса. М. : БИНОМ. Лаборатория знаний, 24 с.

Логические элементы — Википедия

Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательностями «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (в частности, на диодах или транзисторах), пневматическими, гидравлическими, оптическими и другими.

С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам: вначале — на электронных лампах, позже — на транзисторах. После доказательства в 1946 году теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.

Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).

Всего возможно x(xn)∗m{\displaystyle x^{\left(x^{n}\right)*m}} логических функций и соответствующих им логических элементов, где x{\displaystyle x} — основание системы счисления, n{\displaystyle n} — число входов (аргументов), m{\displaystyle m} — число выходов; таким образом, количество теоретически возможных логических элементов бесконечно. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.

Всего возможны 2(22)∗1=24=16{\displaystyle 2^{\left(2^{2}\right)*1}=2^{4}=16} двухвходовых двоичных логических элементов и 2(23)∗1=28=256{\displaystyle 2^{\left(2^{3}\right)*1}=2^{8}=256} трёхвходовых двоичных логических элементов (Булева функция). Аналогично, для троичной логики возможны 19 683 двухвходовых и 7 625 597 484 987 трёхвходовых логических элементов.

Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.

Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.

Унарные операции[править | править код]

Из 2(21)=22=4{\displaystyle 2^{\left(2^{1}\right)}=2^{2}=4} возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания (инверсии) и повторения, причём, операция отрицания имеет бо́льшую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.

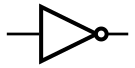
Отрицание (инверсия). Операция «НЕ»[править | править код]

• Инвертор (элемент «НЕ»)
• 
• 

Здесь и далее приведены гра­фи­чес­кие обозначения логических элементов по стандартам IEC (слева) и ANSI (справа).

A{\displaystyle A}	¬A{\displaystyle \neg A}
0	1
1	0

Мнемоническое правило для отрицания звучит так — на выходе будет:

Повторение[править | править код]

A{\displaystyle A}	A{\displaystyle A} (буферизованное)
0	0
1	1

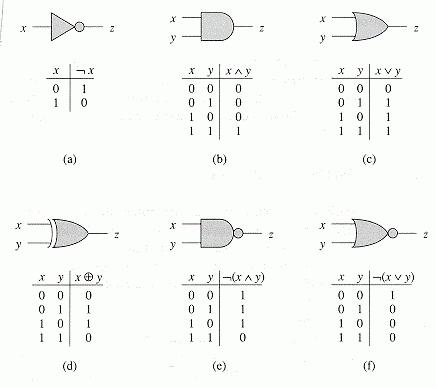
Бинарные операции[править | править код]

Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками. Из 2(22)=24=16{\displaystyle 2^{\left(2^{2}\right)}=2^{4}=16} возможных бинарных логических операций с двумя знаками с унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.

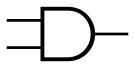
Конъюнкция (логическое умножение). Операция «И»[править | править код]

• Элемент «И»
• 
• 

A{\displaystyle A}	B{\displaystyle B}	A∧B{\displaystyle A\land B}
0	0	0
0	1	0
1	0	0
1	1	1

Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так — на выходе будет:

• «1» тогда и только тогда, когда на всех входах действуют «1»,
• «0» тогда и только тогда, когда хотя бы на одном входе действует «0».

Словесно эту операцию можно выразить следующим выражением: «Истина на выходе может быть только при истине на входе 1 И истине на входе 2».

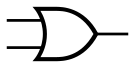
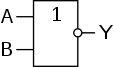
Дизъюнкция (логическое сложение). Операция «ИЛИ»[править | править код]

• Элемент «ИЛИ»
• 
• 

A{\displaystyle A}	B{\displaystyle B}	A∨B{\displaystyle A\lor B}
0	0	0
0	1	1
1	0	1
1	1	1

Мнемоническое правило для дизъюнкции с любым количеством входов звучит так — на выходе будет:

• «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
• «0» тогда и только тогда, когда на всех входах действуют «0».

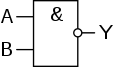
Инверсия функции конъюнкции. Операция «И-НЕ» (штрих Шеффера)[править | править код]

• Элемент «И-НЕ»
• 
• 

A{\displaystyle A}	B{\displaystyle B}	A|B{\displaystyle A|B}
0	0	1
0	1	1
1	0	1
1	1	0

Мнемоническое правило для И-НЕ с любым количеством входов звучит так — на выходе будет:

• «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
• «0» тогда и только тогда, когда на всех входах действуют «1».

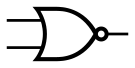
Инверсия функции дизъюнкции. Операция «ИЛИ-НЕ» (стрелка Пирса)[править | править код]

• Элемент «ИЛИ-НЕ»
• 
• 

A{\displaystyle A}	B{\displaystyle B}	A↓B{\displaystyle A\downarrow B}
0	0	1
0	1	0
1	0	0
1	1	0

Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так — на выходе будет:

• «1» тогда и только тогда, когда на всех входах действуют «0»,
• «0» тогда и только тогда, когда хотя бы на одном входе действует «1».

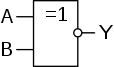
Эквивалентность (равнозначность). Операция «исключающее ИЛИ-НЕ»[править | править код]

• Элемент «исключающее ИЛИ-НЕ»
• 
• 

A{\displaystyle A}	B{\displaystyle B}	A↔B{\displaystyle A\leftrightarrow B}
0	0	1
0	1	0
1	0	0
1	1	1

Мнемоническое правило эквивалентности с любым количеством входов звучит так — на выходе будет:

• «1» тогда и только тогда, когда на входе действует чётное количество «1»,
• «0» тогда и только тогда, когда на входе действует нечётное количество «1».

Словесная запись: «истина на выходе при истине на входе 1 и входе 2 или при лжи на входе 1 и входе 2».

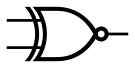
Сложение (сумма) по модулю 2 (неравнозначность, инверсия равнозначности). Операция «исключающее ИЛИ»[править | править код]

• Элемент «исключающее ИЛИ»
• 
• 

A{\displaystyle A}	B{\displaystyle B}	A⊕B{\displaystyle A\oplus B}
0	0	0
0	1	1
1	0	1
1	1	0

Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так — на выходе будет:

• «1» тогда и только тогда, когда на входе действует нечётное количество «1»,
• «0» тогда и только тогда, когда на входе действует чётное количество «1».

Словесное описание: «истина на выходе — при истине только на входе 1, либо при истине только на входе 2».

Импликация от A к B (прямая импликация, инверсия декремента, A<=B)[править | править код]

A{\displaystyle A}	B{\displaystyle B}	A→B{\displaystyle A\rightarrow B}
0	0	1
0	1	1
1	0	0
1	1	1

Мнемоническое правило для инверсии декремента звучит так — на выходе будет:

• «0» тогда и только тогда, когда значение на «B» меньше значения на «A»,
• «1» тогда и только тогда, когда значение на «B» больше либо равно значению на «A».

Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)[править | править код]

A{\displaystyle A}	B{\displaystyle B}	B→A{\displaystyle B\rightarrow A}
0	0	1
0	1	0
1	0	1
1	1	1

Мнемоническое правило для инверсии инкремента звучит так — на выходе будет:

• «0» тогда и только тогда, когда значение на «B» больше значения на «A»,
• «1» тогда и только тогда, когда значение на «B» меньше либо равно значению на «A».

Декремент. Запрет импликации по B. Инверсия импликации от A к B[править | править код]

A{\displaystyle A}	B{\displaystyle B}	f(A,B){\displaystyle f\left(A,B\right)}
0	0	0
0	1	0
1	0	1
1	1	0

Мнемоническое правило для инверсии импликации от A к B звучит так — на выходе будет:

• «1» тогда и только тогда, когда значение на «A» больше значения на «B»,
• «0» тогда и только тогда, когда значение на «A» меньше либо равно значению на «B».

Инкремент. Запрет импликации по A. Инверсия импликации от B к A[править | править код]

A{\displaystyle A}	B{\displaystyle B}	f(A,B){\displaystyle f\left(A,B\right)}
0	0	0
0	1	1
1	0	0
1	1	0

Мнемоническое правило для инверсии импликации от B к A звучит так — на выходе будет:

• «1» тогда и только тогда, когда значение на «B» больше значения на «A»,
• «0» тогда и только тогда, когда значение на «B» меньше либо равно значению на «A».

Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.^{[источник не указан 137 дней]}

Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:

• И, НЕ (2 элемента)
• ИЛИ, НЕ (2 элемента)
• И-НЕ (1 элемент)
• ИЛИ-НЕ (1 элемент).

Для преобразования логических функций в один из названых базисов необходимо применять законы (правила) де Моргана.

Реализация логических элементов возможна при помощи устройств, использующих самые разнообразные физические принципы:

• механические,
• гидравлические,
• пневматические,
• электромагнитные,
• электромеханические,
• электронные,
• оптические.

Физические реализации одной и той же логической функции, а также обозначения для истины и лжи, в разных системах электронных и неэлектронных элементов отличаются друг от друга.

Классификация электронных транзисторных физических реализаций логических элементов[править | править код]

Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:

• РТЛ (резисторно-транзисторная логика)
• ДТЛ (диодно-транзисторная логика)
• ТТЛ (транзисторно-транзисторная логика)

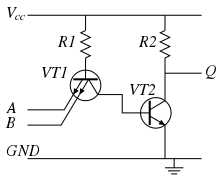Упрощённая схема двухвходового элемента И-НЕ ТТЛ.

Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.

В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.

Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используется в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включённым в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включённым по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало́ и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.

Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4—5 раз (во столько же раз меньше и входной ток логического элемента).

Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10—15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП-технология достигла частот переключения в несколько гигагерц.

Инвертор[править | править код]

Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).

Логические элементы входят в состав микросхем, например ТТЛ-элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.

Комбинационные логические устройства[править | править код]

Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:

Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.

Последовательностные цифровые устройства[править | править код]

Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.

Конъюнкция — Википедия

Конъю́нкция (от лат. conjunctio — «союз, связь») — логическая операция, по смыслу максимально приближенная к союзу «и». Синонимы: логи́ческое «И», логи́ческое умноже́ние, иногда просто «И»^[1].

Конъюнкция может быть бинарной операцией (т. e. иметь два операнда), тернарной операцией (т. e. иметь три операнда), или n-арной операцией (т. e. иметь n операндов).

Наиболее часто встречаются следующие обозначения для операции конъюнкции:

a∧b,a&&b,a&b,a⋅b,aANDb,min(a,b){\displaystyle a\land b,\quad a\And \And b,\quad a\And b,\quad a\cdot b,\quad a\,\,\mathrm {AND} \,\,b,\quad \min(a,b)}

(в случае использования точки, как знака логического умножения, этот знак, как и при обычном умножении в алгебре, может быть опущен: ab{\displaystyle ab}^[1]).

При этом обозначение a∧b{\displaystyle a\land b}, рекомендованное стандартом ISO 31-11, наиболее широко распространено в современной математике и математической логике, где оно, впрочем, конкурирует со знаком амперсанда &^[1]; последний, появившись ещё в I веке до н. э. как графическое сокращение (лигатура) латинского союза et ‘и’, уже Якобом и Иоганном Бернулли в 1685 году использовался в качестве логической связки (у них он, однако, связывал не высказывания, а понятия)^[2][3]. Джордж Буль (а за ним — и другие пионеры систематического применения символического метода к логике: У. С. Джевонс, Э. Шрёдер, П. С. Порецкий) обозначал конъюнкцию знаком ⋅{\displaystyle \cdot } — как обычное умножение^[4]. Символ ⋀ (перевёрнутый знак дизъюнкции) в качестве обозначения конъюнкции был предложен Арендом Гейтингом (1930)^[5].

Обозначение ⋀ для конъюнкции было использовано и в раннем языке программирования Алгол 60^[6]. Однако из-за отсутствия соответствующего символа в стандартных наборах символов (например, в ASCII или EBCDIC), применявшихся на большинстве компьютеров, в получивших наибольшее распространение языках программирования были предусмотрены иные обозначения для конъюнкции. Так, в Фортране IV и PL/I применялись соответственно обозначения .AND. и & (с возможностью замены последнего на ключевое слово AND)^[7]; в языках Паскаль и Ада используется зарезервированное слово and^[8][9]; в языках C и C++ применяются обозначения & для побитовой конъюнкции и && для логической конъюнкции^[10]).

Наконец, при естественном упорядочении значений истинности двузначной логики (когда полагают, что 0<1{\displaystyle 0<1}), оказывается, что (a∧b)=min(a,b).{\displaystyle (a\land b)\,=\,\min(a,b).} Таким образом, конъюнкция оказывается частным случаем операции вычисления минимума; это открывает наиболее естественный способ определить операцию конъюнкции в системах многозначной логики (хотя иногда рассматривают и другие способы обобщения конъюнкции — например, такой: (a∧b)=ab(mod⁡k){\displaystyle (a\land b)\,=\,ab\;(\operatorname {mod} k)} в случае k-значной логики, в которой множество значений истинности представлено начальным отрезком {0,…,k−1}{\displaystyle \{0,\dots ,k-1\}} полугруппы N{\displaystyle \mathbb {N} } натуральных чисел)^[11][12].

Определение.
Логическая функция MIN в двухзначной (двоичной) логике называется конъюнкция (логи́ческое «И», логи́ческое умноже́ние или просто «И»).

Правило: результат равен наименьшему операнду.

Описание.
В булевой алгебре конъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {0,1}{\displaystyle \{0,1\}}. Результат также принадлежит множеству {0,1}{\displaystyle \{0,1\}}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 0,1{\displaystyle 0,1} может использоваться любая другая пара подходящих символов, например false,true{\displaystyle false,true} или F,T{\displaystyle F,T} или «ложь», «истина», но при таком обозначении необходимо дополнительно доопределять старшинство, например, true>false{\displaystyle true>false}, при цифровом обозначении старшинство естественно 1>0{\displaystyle 1>0}.
Правило: результат равен 1{\displaystyle 1}, если все операнды равны 1{\displaystyle 1}; во всех остальных случаях результат равен 0{\displaystyle 0}.

Таблицы истинности:
для бинарной конъюнкции

для тернарной конъюнкции

a{\displaystyle a}	b{\displaystyle b}	c{\displaystyle c}	a∧b∧c{\displaystyle a\land b\land c}
0	0	0	0
1	0	0	0
0	1	0	0
1	1	0	0
0	0	1	0
1	0	1	0
0	1	1	0
1	1	1	1

Конъюнкция коммутативна, ассоциативна и дистрибутивна по отношению к слабой дизъюнкции^[13].

Операции, называемой в двоичной логике конъюнкция, в многозначных логиках обычно сопоставляется операция минимум: min(a,b){\displaystyle min(a,b)}, где a,b∈{0,…,k−1},{\displaystyle a,b\in \{0,\dots ,k-1\},} а k{\displaystyle k} — значность логики; впрочем, возможны и другие варианты обобщения обычной конъюнкции на многозначный случай. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов 0{\displaystyle 0} и k−1{\displaystyle k-1}.

Следует отметить, что название этой операции минимум имеет смысл в логиках с любой значностью, в том числе и в двоичной логике, а названия конъюнкция, логи́ческое «И», логическое умноже́ние и просто «И» характерны для двоичной логики, а при переходе к многозначным логикам используются реже.

В классическом исчислении высказываний свойства конъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства конъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для конъюнкции:
a∧b→a{\displaystyle a\land b\to a}
a∧b→b{\displaystyle a\land b\to b}
a→(b→(a∧b)){\displaystyle a\to (b\to (a\land b))}

С помощью этих аксиом можно доказать другие формулы, содержащие операцию конъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.

Логический элемент «И»

Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения^[13]. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на всех входах есть «1»,
• «0» тогда и только тогда, когда хотя бы на одном входе есть «0»

С точки зрения теории множеств, конъюнкция аналогична операции пересечения.

В компьютерных языках используется два основных варианта конъюнкции: логическое «И» и побитовое (поразрядное) «И». Например, в языках C/C++ логическое «И» обозначается символом «&&», а побитовое — символом «&». В терминологии, используемой в C#, операцию «&» принято называть логическим «И», а операцию «&&» — условным «И», поскольку значения операндов являются условиями для продолжения вычисления. В языках Pascal/Delphi оба вида конъюнкции обозначаются с использованием ключевого слова «and», а результат действия определяется типом операндов. Если операнды имеют логический тип (например, Boolean) — выполняется логическая операция, если целочисленный (например, Byte) — поразрядная.

Логическое «И» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата false{\displaystyle false} или true{\displaystyle true}. Например:

if (a & b & c) 
{
    /* какие-то действия */
};

Сравнение в данном случае будет продолжаться до конца выражения, независимо от промежуточных результатов. Принцип работы условного «И» в аналогичной ситуации:

a = false; b = true; c = true;
if (a && b && c) 
{
    /* какие-то действия */ 
};

Проверка истинности выражения в данном случае остановится после проверки переменной a, так как дальнейшее сравнение не имеет смысла.

Результат будет равен true{\displaystyle true}, если оба операнда равны true{\displaystyle true} (для числовых типов не равны 0{\displaystyle 0}). В любом другом случае результат будет равен false{\displaystyle false}.

При этом применяется стандартное соглашение: если значение левого операнда равно false{\displaystyle false}, то значение правого операнда не вычисляется (вместо b{\displaystyle b} может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приёмом в некоторых случаях. Компилятор Delphi поддерживает специальную директиву, включающую

или выключающую

подобное поведение. Например, если левый операнд проверяет возможность вычисления правого операнда:

if (a != 0 && b / a > 3) 
{
    /* какие-то действия */
};

В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдет деления на ноль.

Побитовое «И» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,

если
a =	011001012{\displaystyle 01100101_{2}}
b =	001010012{\displaystyle 00101001_{2}}
то
a И b =	001000012{\displaystyle 00100001_{2}}

Часто указывают на сходство между конъюнкцией и союзом «и» в естественном языке. Составное утверждение «A и B» считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как 0{\displaystyle 0}. При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз «и» может нести дополнительный оттенок «и тогда», «и поэтому», «и потом». Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке «Мэри вышла замуж и родила ребенка» — не то же самое, что «Мэри родила ребенка и вышла замуж».

1. ↑ ^{1 2 3} Кондаков, 1975, с. 264—266, 534—536.
2. ↑ Ampersand (неопр.). // Website Online Etymology Dictionary. Дата обращения 7 февраля 2016.
3. ↑ Кондаков, 1975, с. 67.
4. ↑ Стяжкин Н. И. . Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 321, 348, 352, 368.
5. ↑ Earliest Uses of Symbols of Set Theory and Logic (неопр.). // Website Jeff Miller Web Pages. Дата обращения 7 февраля 2016.
6. ↑ Кондаков, 1975, с. 30.
7. ↑ Пратт Т. . Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
8. ↑ Грогоно П. . Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
9. ↑ Вегнер П. . Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
10. ↑ Эллис М.^[en], Строуструп Б. . Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
11. ↑ Яблонский С. В. . Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
12. ↑ Рвачёв В. Л. . Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.
13. ↑ ^{1 2} Словарь по кибернетике. 2-е изд / Под ред. В. С. Михалевича. — Киев: Украинская советская энциклопедия, 1989. — 751 с. — ISBN 5-88500-008-5.

Формальная
Математическая (теоретическая, символическая)	Высказывание — построение над множеством {B,¬,∧,∨,0,1}{\displaystyle \{B,\neg ,\land ,\lor ,0,1\}} 2 константы 0 1
См. также

Простейшие логические операции в информатике

Каждого, кто начинает изучать информатику, учат двоичной системе исчисления. Именно она используется для вычисления логических операций. Рассмотрим ниже все самые элементарные логические операции в информатике. Ведь если задуматься, именно они используются при создании логики вычислительных машин и приборов.

Отрицание

Перед тем как начать подробно рассматривать конкретные примеры, перечислим основные логические операции в информатике:

• отрицание;
• сложение;
• умножение;
• следование;
• равенство.

Также перед началом изучения логических операций стоит сказать, что в информатике ложь обозначается «0», а правда «1».

Для каждого действия, как и в обычной математике, используются следующие знаки логических операций в информатике: ¬, v, &, ->.

Каждое действие возможно описать либо цифрами 1/0, либо просто логическими выражениями. Начнём рассмотрение математической логики с простейшей операции, использующей всего одну переменную.

Логическое отрицание — операция инверсии. Суть заключается в том, что если исходное выражение — истина, то результат инверсии — ложь. И наоборот, если исходное выражение — ложь, то результатом инверсии станет — правда.

При записи этого выражения используется следующее обозначение «¬A».

Приведём таблицу истинности — схему, которая показывает все возможные результаты операции при любых исходных данных.

Таблица истинности для инверсии

А	х	о
¬A	о	х

То есть, если у нас исходное выражение — истина (1), то его отрицание будет ложным (0). А если исходное выражение — ложь (0), то его отрицание — истина (1).

Сложение

Оставшиеся операции требуют наличия двух переменных. Обозначим одно выражение —

А, второе — В. Логические операции в информатике, обозначающие действие сложения (или дизъюнкция), при написании обозначаются либо словом «или», либо значком «v». Распишем возможные варианты данных и результаты вычислений.

1. Е=1, Н=1 ,тогда Е v Н = 1. Если оба выражения истинны, тогда и их дизъюнкция также истинна.
2. Е=0, Н=1 ,в итоге Е v Н = 1. Е=1, Н=0 , тогда Е v Н= 1. Если хотябы одно из выражений истинно, тогда и результат их сложения будет истиной.
3. Е=0, Н=0 ,результат Е v Н = 0. Если оба выражения ложны, то их сумма также — ложь.

Для краткости создадим таблицу истинности.

Дизъюнкция

Е	х	х	о	о
Н	х	о	х	о
Е v Н	х	х	х	о

Умножение

Разобравшись с операцией сложения, переходим к умножению (конъюнкции). Воспользуемся теми же обозначениями, которые были приведены выше для сложения. При письме логическое умножение обозначается значком «&», либо буквой «И».

1. Е=1, Н=1 ,тогда Е & Н = 1. Если оба выражения истинны, тогда их конъюнкция — истина.
2. Если хотя бы одно из выражений — ложь, тогда результатом логического умножения также будет ложь.

• Е=1, Н=0, поэтому Е & Н = 0.
• Е=0, Н=1, тогда Е & Н = 0.
• Е=0, Н=0, итог Е & Н = 0.

Конъюнкция

Е	х	х	0	0
Н	х	0	х	0
Е & Н	х	0	0	0

Следствие

Логическая операция следования (импликация) — одна из простейших в математической логике. Она основана на единственной аксиоме — из правды не может следовать ложь.

1. Е=1, Н=, поэтому Е -> Н = 1. Если пара влюблена, то они могут целоваться — правда.
2. Е=0, Н=1, тогда Е -> Н = 1. Если пара не влюблена, то они могут целоваться — также может быть истиной.
3. Е=0, Н=0, из этого Е -> Н = 1. Если пара не влюблена, то они и не целуются — тоже правда.
4. Е=1, Н=0, результатом будет Е -> Н = 0. Если пара влюблена, то они не целуются — ложь.

Для облегчения выполнения математических действий также приведём таблицу истинности.

Импликация

Е	х	х	о	о
Н	х	о	х	0
Е -> Н	х	о	х	х

Равенство

Последней рассмотренной операцией станет логическое тождественное равенство или эквивалентность. В тексте оно может обозначаться как «…тогда и только тогда, когда…». Исходя из этой формулировки, напишем примеры для всех исходных вариантов.

1. А=1, В=1, тогда А≡В = 1. Человек пьёт таблетки тогда и только тогда, когда болеет. (истина)
2. А=0, В=0, в итоге А≡В = 1. Человек не пьёт таблетки тогда и только тогда, когда не болеет. (истина)
3. А=1, В=0, поэтому А≡В = 0. Человек пьёт таблетки тогда и только тогда, когда не болеет. (ложь)
4. А=0, В=1 ,тогда А≡В = 0. Человек не пьёт таблетки тогда и только тогда, когда болеет. (ложь)

Эквивалентность

А	х	о	х	о
В	х	о	0	х
А≡В	х	х	о	о

Свойства

Итак, рассмотрев простейшие логические операции в информатике, можем приступить к изучению некоторых их свойств. Как и в математике, у логических операций существует свой порядок обработки. В больших логических выражениях операции в скобках выполняются в первую очередь. После них первым делом подсчитываем все значения отрицания в примере. Следующим шагом станет вычисление конъюнкции, а затем дизъюнкции. Только после этого выполняем операцию следствия и, наконец, эквивалентности. Рассмотрим небольшой пример для наглядности.

А v В & ¬В -> В ≡ А

Порядок выполнения действий следующий.

1. ¬В
2. В&(¬В)
3. А v(В&(¬В))
4. (А v(В&(¬В)))->В
5. ((А v(В&(¬В)))->В)≡А

Для того чтобы решить этот пример, нам потребуется построить расширенную таблицу истинности. При её создании помните, что столбцы лучше располагать в том же порядке, в каком и будут выполняться действия.

Решение примера

А	В	¬В	В&(¬В)	А v(В&(¬В))	(А v(В&(¬В)))->В	((А v(В&(¬В)))->В)≡А
х	о	х	о	х	х	х
х	х	о	о	х	х	х
о	о	х	о	о	х	о
о	х	о	о	о	х	о

Как мы видим, результатом решения примера станет последний столбец. Таблица истинности помогла решить задачу с любыми возможными исходными данными.

Заключение

В этой статье были рассмотрены некоторые понятия математической логики, такие как информатика, свойства логических операций, а также — что такое логические операции сами по себе. Были приведены некоторые простейшие примеры для решения задач по математической логике и таблицы истинности, необходимые для упрощения этого процесса.

Импликация — Википедия

Импликация (от лат. implicatio — «связь») — бинарная логическая связка, по своему применению приближенная к союзам «если…, то…».

Импликация записывается как посылка ⇒{\displaystyle \Rightarrow } следствие; применяются также стрелки другой формы и направленные в другую сторону, но всегда указывающие на следствие.

Суждение, выражаемое импликацией, выражается также следующими способами^[1][2]:

Импликация играет очень важную роль в умозаключениях. С её помощью формулируются определения различных понятий, теоремы, научные законы^[3].

При учёте смыслового содержания высказываний импликация подразумевает причинную связь между посылкой и заключением^[4].

В булевой логике импликация — это функция двух переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {0,1}{\displaystyle \{0,1\}}. Результат также принадлежит множеству {0,1}{\displaystyle \{0,1\}}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 0,1{\displaystyle 0,1} может использоваться любая другая пара подходящих символов, например false,true{\displaystyle \operatorname {false} ,\operatorname {true} } или F,T{\displaystyle F,T} или «ложь», «истина».

Правило:

Импликация как булева функция ложна лишь тогда, когда посылка истинна, а следствие ложно. Иными словами, импликация A→B{\displaystyle A\to B} это сокращённая запись для выражения ¬A∨B{\displaystyle \neg A\lor B}.

Таблицы истинности:

прямая импликация (от a к b) (материальная импликация (англ.)русск., материальный кондиционал (англ.)русск.)

• если первый операнд не больше второго операнда, то 1,
• если a⩽b{\displaystyle a\leqslant b}, то истинно (1).

«Житейский» смысл импликации. Для более лёгкого понимания смысла прямой импликации и запоминания её таблицы истинности может пригодиться житейская модель:

А — начальник. Он может приказать «работай» (1) или сказать «делай что хочешь» (0).

В — подчиненный. Он может работать (1) или бездельничать (0).

В таком случае импликация — не что иное, как послушание подчиненного начальнику. По таблице истинности легко проверить, что послушания нет только тогда, когда начальник приказывает работать, а подчиненный бездельничает.

обратная импликация (англ.)русск. (от b к a, A∨(¬B){\displaystyle A\lor (\neg B)})

• если первый операнд не меньше второго операнда, то 1,
• если a⩾b{\displaystyle a\geqslant b}, то истинно (1).

Обратная импликация — отрицание (негация, инверсия) обнаружения увеличения (перехода от 0 к 1, инкремента).

отрицание (инверсия, негация) прямой импликации

• если первый операнд больше второго операнда, то 1,
• если a>b{\displaystyle a>b}, то истинно (1).

отрицание (инверсия, негация) обратной импликации (англ.)русск. (¬A∧B{\displaystyle \lnot A\land B}), разряд займа в двоичном полувычитателе.

• если первый операнд меньше второго операнда, то 1,
• если a<b{\displaystyle a<b}, то истинно (1).

Другими словами, две импликации (прямая и обратная) и две их инверсии — это четыре оператора отношений. Результат операций зависит от перемены мест операндов.

Синонимические импликации выражения в русском языке[править | править код]

• Если А, то Б
• Б в том случае, если А
• При А будет Б
• Из А следует Б
• В случае А произойдет Б
• Б, так как А
• Б, потому что А
• А — достаточное условие для Б
• Б — необходимое условие для А

Импликация высказываний означает, что одно из них следует из другого. Импликация обозначается символом ⇒{\displaystyle \Rightarrow }, и ей соответствует вложение множеств: пусть A⊂B{\displaystyle A\subset B}, тогда

x∈A⇒x∈B.{\displaystyle x\in A\Rightarrow x\in B.}

Например, если A{\displaystyle A} — множество всех квадратов, а B{\displaystyle B} — множество прямоугольников, то, конечно, A⊂B{\displaystyle A\subset B} и

(a — квадрат) ⇒{\displaystyle \Rightarrow } (a — прямоугольник).

(если a является квадратом, то a является прямоугольником).

В классическом исчислении высказываний свойства импликации определяются с помощью аксиом.

Можно доказать эквивалентность импликации A→B{\displaystyle A\rightarrow B} формуле ¬A∨B{\displaystyle \neg A\lor B} (с первого взгляда более очевидна её эквивалентность формуле ¬(A∧¬B){\displaystyle \neg (A\land \neg B)}, которая принимает значение «ложь» в случае, если выполняется A (посылка), но не выполняется B (следствие)). Поэтому любое высказывание можно заменить на эквивалентное ему без знаков импликации.

В интуиционистской логике импликация никоим образом не сводится к отрицаниям. Скорее напротив, отрицание ¬A можно представить в виде A→⊭{\displaystyle A\rightarrow \nvDash }, где ⊭{\displaystyle \nvDash } — пропозициональная константа «ложь». Впрочем, такое представление отрицания возможно и в классической логике.

В интуиционистской теории типов импликации соответствует множество (тип) отображений из A в B.

В учении о силлогизмах импликации отвечает «общеутвердительное атрибутивное высказывание».

В языках программирования импликация используется, как правило, неявно. Например, конструкция, предполагающая истинность условий B в данном участке программы:

 if (!(выражение A) || выражение B) {
    сделать_что-то_полезное
 } else {
    сбой
 }

будет успешно выполняться тогда и только тогда, когда верна импликация A → B. В то же время эти условия можно спокойно написать в одной строке, объединив их оператором конъюнкции.

 if (выражение A) and (выражение B) {
    сделать_что-то_полезное
 }

При стандартных опциях компилятора (Delphi, C++ Builder)^{[прояснить]} проверка идёт до тех пор, пока результат не станет очевидным, и если А ложно, то (А и В) ложно вне зависимости от В, и не нужно ставить ещё один условный оператор.

 //выражение A - ложно
 if (выражение A) {
    // Дальше проверка не идёт
    ... if (выражение B) {
       сделать_что-то_полезное
    } ...
 }

В функциональных языках импликация может быть не только правилом вычислений, но и видом отношения между данными, то есть обрабатываться (в том числе и выполняться) и создаваться по ходу выполнения программы.

• Эдельман С.Л. Математическая логика. — М.: Высшая школа, 1975. — 176 с.
• Игошин В.И. Задачник-практикум по математической логике. — М.: Просвещение, 1986. — 158 с.
• Гиндикин С.Г. Алгебра логики в задачах. — М.: Наука, 1972. — 288 с.
• Барабанов О.О. Импликация / Труды XI международных Колмогоровских чтений: сборник статей. – Ярославль: Изд-во ЯГПУ, 2013. С.49-53.

Конспект «Логические значения, операции, выражения»

Логические значения, операции, выражения

Код ОГЭ: 1.3.3. Логические значения, операции, выражения

Алгебра логики, логические высказывания

Наука, изучающая формы, методы и законы правильного мышления, называется логикой. Она интересуется не содержанием мышления, а его формой, поэтому ее часто называют еще формальной логикой.

Форма мышления — это способ выражения мыслей или форма, по которой они строятся.

Форма, обозначающая какой–либо объект или отличающий его признак, называется понятием. Примеры понятий: «компьютер», «планета», «длина», «профессия».

Форма, утверждающая или отрицающая что–либо о свойствах понятий и отношений между ними, называется утверждением (высказыванием, суждением). Примеры логических утверждений: «Декодирование — процесс восстановления информации из закодированного представления»; «В двоичной системе используются две цифры: 0 и 1»; «Париж — столица Франции». Утверждения могут быть истинными или ложными. Так, высказывание «Шанхай — столица Франции» является ложным утверждением.

Форма, в которой из двух или нескольких высказываний получают новое утверждение, называется умозаключением. Пример умозаключения: «Периферийные устройства компьютера — это устройства для ввода или вывода информации. Сканер — устройство для переноса текста и изображений с бумаги в компьютер. Следовательно, сканер — периферийное устройство».

Правила, которые должны соблюдаться, чтобы на основании истинных суждений получить истинные выводы, — это законы мышления. Логика изучает эти законы и способы получения новых утверждений на основании уже имеющихся.

Математическая логика использует для установления истинности или ложности высказываний математические методы. Она пользуется специальным символьным языком, подобным языку математики, поэтому ее часто называют символьной логикой.

Алгебра логики — раздел математической логики, в котором методы алгебры используются в логических преобразованиях. Она изучает логические высказывания и методы установления их истинности или ложности с помощью алгебраических методов.

Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно. Вопросительные и повелительные предложения не являются логическими высказываниями. Но и не каждое повествовательное предложение является логическим высказыванием. Например, суждение «Лето было очень дождливым» не является однозначным, для утверждения «Существует несколько Вселенных» нельзя однозначно определить истинность; поэтому такие предложения не являются логическими высказываниями (утверждениями).

Таким образом, отличительной особенностью логических высказываний является возможность принимать одно из двух значений — истина и ложь. Истинность или ложность высказывания определяется вне алгебры логики — с помощью наблюдений, научных исследований, практических опытов и т. п.

В алгебре логики различают простые высказывания и сложные (составные), составленные из нескольких простых. Если в высказывании нельзя выделить некую часть, которая не совпадает по смыслу с исходным высказыванием и сама является высказыванием, то оно называется простым высказыванием. Простые высказывания обычно обозначаются латинскими буквами A, B, C и т. д.

Сложные высказывания представляют собой объединение простых высказываний с помощью логических связок. В качестве логических связок используются слова «не», «и», «или», «тогда и только тогда», «если … то». Истинность или ложность получаемых таким образом сложных высказываний определяется значением простых высказываний. Например, из простых высказываний «Офис фирмы находится в Мадриде» и «Офис фирмы находится в Берлине» можно составить сложные: «Офис фирмы находится в Мадриде или Берлине», «Офис фирмы находится в Мадриде и Берлине», «Если офис фирмы находится в Мадриде, то он находится в Берлине». Истинность первого из них означает, что офис фирмы находится в одном из названных городов или же имеются офисы в обоих городах. Ложность его означает, что ни в одном из этих городов офиса нет. Второе составное утверждение истинно тогда, когда в обоих городах имеется офис фирмы. Если же офис существует только в Берлине или только в Мадриде, — второе составное высказывание ложно.

В классической, двузначной алгебре логики логических значений всего два: истина (True) и ложь (False). Им соответствует цифровое представление — 1 и 0. Иногда эти значения записывают как «да» и «нет». Факт истинности или ложности некоторого высказывания А записывают соответственно как А = 1 или А = 0.

Логические операции

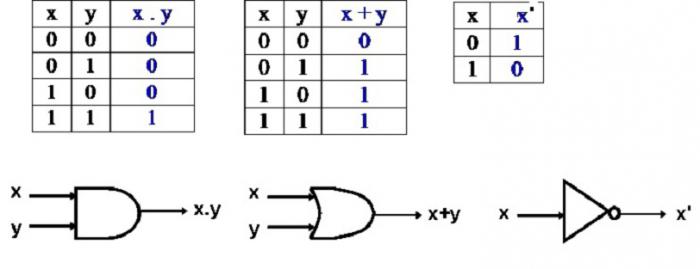
В алгебре логики логические связки рассматриваются как логические операции. Они имеют свои названия и обозначения. Результаты применения каждой операции к логическим высказываниям (истинным или ложным) можно представить в виде таблицы. В ней указывают все возможные сочетания значений исходных логических высказываний и истинность или ложность результата. Такие таблицы называют таблицами истинности операции. Обычно в них используют обозначения логических значений 0 и 1 или ложь и истина.

Основные логические операции — отрицание, конъюнкция, дизъюнкция, исключающая дизъюнкция, следование, эквивалентность.

Логическое отрицание (инверсия) — логическая операция, в результате которой из данного высказывания получается новое высказывание — отрицание исходного. Обозначается символически чертой сверху (Ā) или условными обозначениями ¬А, not А, не А (читается «отрицание А», «не А», «А ложно», «неверно, что А»).

Высказывание ¬А ложно, когда А истинно, и истинно, когда А ложно.

Таблица истинности операции отрицания

Если обозначить через А высказывание «Арбуз является ягодой», то ¬А соответствует высказыванию «Арбуз не является ягодой» («Неверно, что арбуз — ягода»).

Отрицание является унарной операцией. Унарная (одноместная) операция — это операция, которая применяется к одному операнду.

Остальные логические операции являются двуместными (бинарными). Бинарная (двуместная) операция — это операция, которая выполняется над двумя операндами.

Логическое умножение (конъюнкция) — операция, соединяющая два или более высказываний при помощи связки «и». Эта связка символически обозначается с помощью знака ∧ и читается «А и В». Для обозначения конъюнкции также применяются знаки: А • В, А & В, А и В, А and В, а иногда между высказываниями не ставится никакого знака: АВ.

Высказывание А ∧ В истинно только тогда, когда оба высказывания А и В истинны. Высказывание А ∧ В ложно только тогда, когда ложно хотя бы одно из высказываний А или В.

Таблица истинности операции конъюнкции

Например, высказывания «Лондон расположен севернее Лиссабона» и «Лондон расположен восточнее Лиссабона» истинны. Тогда истинным будет и составное логическое высказывание «Лондон расположен севернее и восточнее Лиссабона». Высказывания «Лондон расположен не севернее и восточнее Лиссабона», «Лондон расположен севернее и не восточнее Лиссабона», «Лондон расположен не севернее и не восточнее Лиссабона» — ложны.

Логическое сложение (дизъюнкция) — операция, соединяющая два или более высказываний при помощи связки « или». Эта связка символически обозначается с помощью знака v и читается «А или В». Для обозначения дизъюнкции также применяются знаки: А + В, А или В, А or В, А | B.

Высказывание А v В истинно только тогда, когда хотя бы одно из высказываний А или В истинно. Высказывание А v В ложно только тогда, когда оба высказывания А и В ложны.

Таблица истинности операции дизъюнкции

Например, высказывания «Виктор старше Ольги» и «Виктор — однофамилец Ольги» истинны. Тогда истинными будут и составные логические высказывания «Виктор старше Ольги или Виктор — однофамилец Ольги», «Виктор младше Ольги или Виктор — однофамилец Ольги», «Виктор старше Ольги или Виктор — не однофамилец Ольги». Высказывание «Виктор младше Ольги или Виктор — не однофамилец Ольги» — ложно, поскольку ложны оба составляющие его простые высказывания.

Исключающее сложение (исключающая дизъюнкция, строгая дизъюнкция, сложение по модулю два, дизъюнкция строго–разделительная) — логическая операция, соединяющая два высказывания при помощи связки «или», употребленной в исключающем смысле (называется также исключающее «или»). Операция символически обозначается с помощью знака ⊕ и читается «либо А, либо В».

Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.

Таблица истинности операции строгой дизъюнкции

Например, результат исключающей дизъюнкции двух высказываний «Виктор не старше Ольги» и «Виктор младше Ольги» всегда будет истиной, кто бы из них не был старше.

Логическое следование (импликация) — логическая операция, соединяющая два высказывания при помощи связки «если… то» в сложное высказывание. Операция символически обозначается с помощью знака → и читается «Если А, то В», «А влечет В», «из А следует В», «А имплицирует В». Для обозначения импликации применяются также знаки ⊃ или ⇒. Первое логическое высказывание является условием (посылкой), а второе — следствием (заключением).

Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина. Таким образом, импликация А → В ложна только тогда, когда А истинно, а В ложно (из истинного высказывания следует ложное). Во всех остальных случаях импликация истинна.

Таблица истинности операции импликации

Для высказываний «Луна — спутник Земли» и «Сумма углов треугольника не равна 180°» (первое истинно, второе ложно) составное высказывание «Если Луна — спутник Земли, то сумма углов треугольника не равна 180°» будет ложным. Однако истинными будут высказывания «Если Луна — спутник Земли, то сумма углов треугольника равна 180°», «Если Луна — не спутник Земли, то сумма углов треугольника не равна 180°» и «Если Луна — не спутник Земли, то сумма углов треугольника равна 180°». Этот пример наглядно демонстрирует, что в алгебре логики смысл высказываний не учитывается, а рассматриваются только их истинность или ложность.

Логическое равенство (эквивалентность, следование, двойная импликация, равнозначность) — логическая операция, позволяющая из двух высказываний А и В получить новое высказывание А ≡ В (читается «А эквивалентно B»). Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Для обозначения эквивалентности применяются знаки ~, ⇔.

Если оба высказывания имеют различные логические значения, результатом операции эквивалентности всегда будет ложь. Если же оба простые высказывания ложны или оба истинны, то составное логическое высказывание всегда будет истинно.

Таблица истинности операции эквивалентности

Для высказываний «Линейное уравнение всегда имеет решение» и «Кит — млекопитающее» их эквивалентность всегда будет истиной, так как оба простые утверждения истинны.

Таким образом, сводная таблица истинности для всех основных логических операций имеет вид:

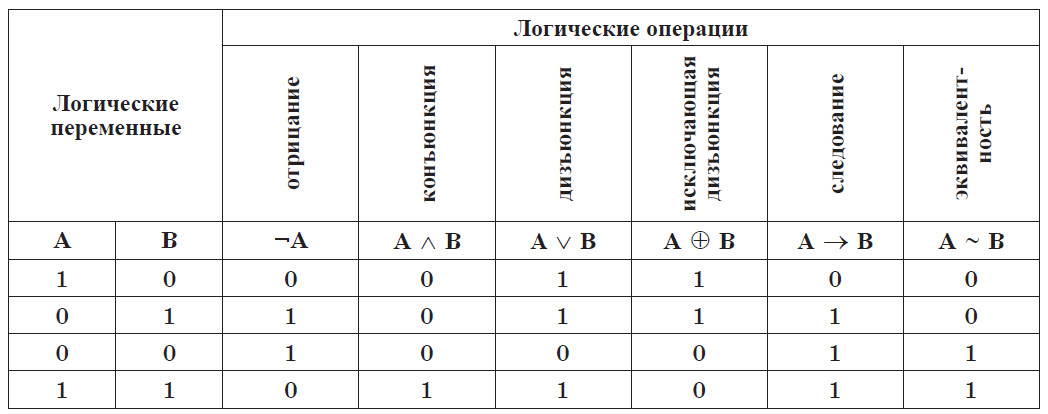
Логические выражения

Логические высказывания могут быть записаны в виде формул (логических выражений). Логические выражения включают логические переменные, знаки логических операций, логические константы (истина и ложь) и скобки. Логические выражения принимают значения истина или ложь.

Правила построения логических выражений:

• любая логическая переменная или константа (истина и ложь) являются логическим выражением;
• если А — , то ¬А — тоже логическое выражение;
• если А и В — логические выражения, то А ∧ В; А v В ; А ⊕ В; А → В; А ~ В — тоже логические выражения.

Например, A ⊕ истина v В v ложь — логическое выражение; А v ⊕ В v ложь не является логическим выражением.

Логическое выражение, принимающее значение истина при любых значениях входящих в него переменных, называется тождественно–истинным выражением (тавтологией). Например, А v В v ¬А; (А ∧ ¬А) → В.

Логическое выражение, принимающее значение ложь при любых значениях входящих в него переменных, называется тождественно–ложным выражением (противоречием). Например, А ∧ ¬А; В ~ ¬В.

Логическое выражение, принимающее как значение ложь, так и значение истина при разных значениях входящих в него переменных, называется выполнимым выражением.

ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ

Для сложных логических выражений, содержащих несколько логических операций, определен порядок выполнения действий (приоритет): сначала операции отрицания, затем операции логического умножения, потом операции логического сложения и исключающего сложения, последними выполняются операции импликации и эквивалентности. Операции выполняются слева направо. Порядок выполнения может быть изменен с помощью скобок.

Приоритет выполнения логических операций в логических выражениях

Пример 1
Определить порядок выполнения логических операций в выражении.
Вычислить его значение, если А = 1, В = 0, С = 1.
¬А ∧ С v (A ⊕ В) ∧ В

Решение. Первыми вычисляются значения в скобках. Затем выполняются операции по приоритетам: самый высокий приоритет имеет операция отрицания, после нее, как в математике, следуют операции умножения, а затем сложения. Таким образом, порядок будет следующий: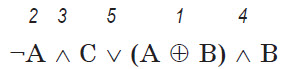

Тогда значение выражения ¬1 ∧ 1 v (1 ⊕ 0) ∧ 0 после вычисления отрицания и выражения в скобках: 0 ∧ 1 v 1 ∧ 0, после операций умножения: 0 v 0. Итог: 0.
Ответ: логическое выражение ложно.

Пример 2
Для каких из приведенных слов истинно следующее высказывание?
(Вторая буква гласная) ИЛИ (Первая буква гласная) И НЕ (Длина имени не больше 5 букв)

1) Олег   2) Марианна  3) Светлана   4) Ольга.

Решение.

1.  В соответствии с приоритетом выполнения операций сначала нужно вычислить результат операции отрицания: «Длина имени больше 5 букв». Такие имена — Марианна, Светлана.
2. Затем необходимо рассчитать результат конъюнкции (связка И) второго и третьего высказываний. Конъюнкция истинна только тогда, когда истинны оба высказывания. Следовательно, нужно выбрать имена, в которых и первая буква гласная, и длина имени больше 5 букв — таких имен среди вариантов нет.
3. Результат дизъюнкции (связка ИЛИ) истинен только тогда, когда истинно или одно, или второе, или одновременно оба простые высказывания. Первое простое высказывание истинно для имени Марианна, второе ложно для указанных имен. Таким образом, верный вариант ответа — 2.

Ответ: 2) Марианна.

СВЯЗЬ МЕЖДУ ЛОГИЧЕСКИМИ ОПЕРАЦИЯМИ

Между логическими операциями существует взаимосвязь. Операции исключающего «или», следования и эквивалентности можно выразить через операции отрицания, логического сложения и умножения, что отражено в следующей таблице.

Связь между логическими операциями

Поэтому операции отрицания, логического сложения и логического умножения называют основными логическими операциями: их достаточно, чтобы построить любое логическое выражение.

Если логическое выражение содержит только операции отрицания, логического сложения и логического умножения, говорят, что выражение находится в нормальной форме.

РАВНОСИЛЬНЫЕ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ

Логические выражения, значения которых совпадают для всех наборов входящих в них переменных, называются равносильными, или эквивалентными.

Чтобы убедиться, что два выражения равносильны, можно построить для них таблицы истинности. Если в таблицах совпадут все значения, значит, выражения равносильны.

Пример 3
Проверить равносильность выражений А ~ E и (Ā ∧ Ē) v (A ∧ E).

Решение. Для проверки следует создать таблицу истинности, содержащую столько строк, сколько возможно наборов значений переменных, входящих в выражение. Для двух переменных (А и E) количество наборов равно четырем. К двум столбцам для значений переменных (А и E) нужно присовокупить количество столбцов, равное количеству операций в выражении. Таким образом, необходимо создать таблицу, содержащую 4 строки и 7 столбцов.

Заполним первые 2 столбца (А и E) всеми сочетаниями значений переменных. Запишем в качестве заголовков столбцов все операции выражения в порядке их выполнения (в соответствии с приоритетами и скобками). Рассчитаем значения этих операций: сначала выражения в скобках, затем результат их сложения.

Последний столбец содержит результирующее значение выражения. Он совпадает с таблицей истинности для операции эквивалентности. Следовательно, выражения равносильны.

Основные законы алгебры логики

Для сложных логических выражений с большим числом переменных определение их истинности путем построения таблиц истинности становится громоздким. В таких случаях применяют способы упрощения выражений. Под упрощением понимают равносильное преобразование выражения к его нормальной форме.

Нормальная форма выражения содержит только операции отрицания, конъюнкции и дизъюнкции и не содержит отрицания выражений и двойных отрицаний.

Для упрощения используют равносильные преобразования, которые иначе называют основными законами алгебры логики.

Тождественные преобразования логических выражений

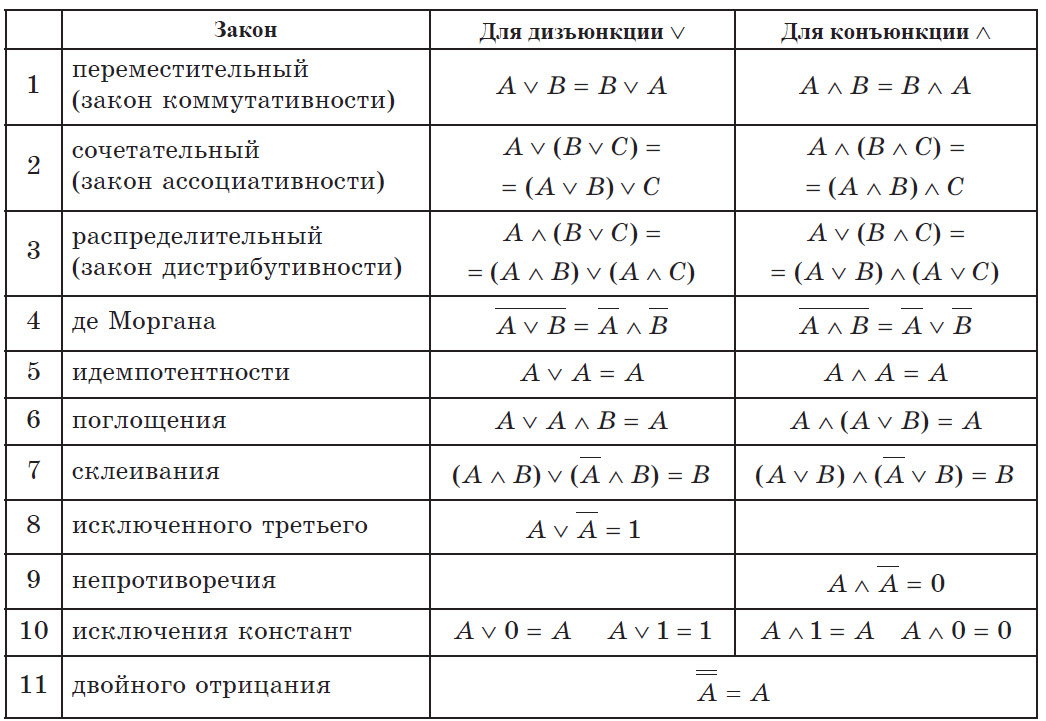
Для всех тождественных преобразований выполняется закон двойственности: если в формуле преобразования заменить конъюнкцию на дизъюнкцию, дизъюнкцию — на конъюнкцию, значения 1 — на 0, 0 — на 1, то закон, сформулированный для конъюнкции, примет форму аналогичного закона для дизъюнкции, и наоборот.

Прежде всего при равносильных преобразованиях избавляются от отрицания выражений, потом — от логических операций исключающей дизъюнкции, следования и эквивалентности. Затем используют законы алгебры логики для уменьшения количества переменных в выражении.

Пример 4
Выбрать выражение, которое равносильно выражению (A ∧ B) v (Ā ∧ B).

1) A         2) A ∧ B          3) Ā ∧ B           4) B

Решение. В соответствии с законом склеивания (A ∧ B) v (Ā ∧ B) = B, следовательно, исходное выражение равносильно выражению В.
Ответ: 4) В.

ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ

Выражения, которые принимают логические значения (истина или ложь) в результате выполнения операций сравнения (больше >, меньше <, больше или равно ≥, меньше или равно ≤, равно =, не равно ≠), также являются логическими выражениями. Кроме операций сравнения и логических операций такие выражения могут включать функции и алгебраические операции. Приоритет выполнения этих операций таков:

1. Вычисление значений функций.
2. Выполнение алгебраических операций (вначале возведение в степень, затем умножение и деление, после чего вычитание и сложение).
3. Выполнение операций сравнения (в порядке записи).
4. Выполнение логических операций (сначала операции отрицания, затем операции логического умножения, потом операции логического сложения, последними выполняются операции импликации и эквивалентности).

Если в логическом выражении используются скобки, то сначала выполняются заключенные в них операции.

Пример 5
Для какого из приведенных ниже значений числа М истинно следующее выражение?
¬М ≥ 10 ∧ M > 3

1) 1          2) 2         3) 3        4) 4

Решение. В соответствии с приоритетами операций сначала следует выполнить операции сравнения, затем отрицания, а потом — конъюнкцию. Отрицанием высказывания М ≥ 10 является высказывание М < 10. Получим выражение М < 10 ∧ M > 3. Для того чтобы это выражение (конъюнкция) было истинным, должны выполняться (т. е. быть истинными) оба неравенства. Следовательно, значение М должно быть больше 3, но меньше 10. Среди предложенных значений этому условию удовлетворяет только одно — число 4.
Ответ: 4) 4.

Задачи, подобные предыдущему примеру, можно решать и с помощью таблиц истинности.

Пример 6.
Для какого из приведенных ниже значений числа М истинно следующее выражение?
¬М ≥ 10 ∧ M > 3

1) 1           2) 2         3) 3        4) 4

Решение. Составим таблицу истинности: все операции выражения укажем в столбцах таблицы, все предложенные значения М укажем в ее строках. Рассчитаем значения таблицы:

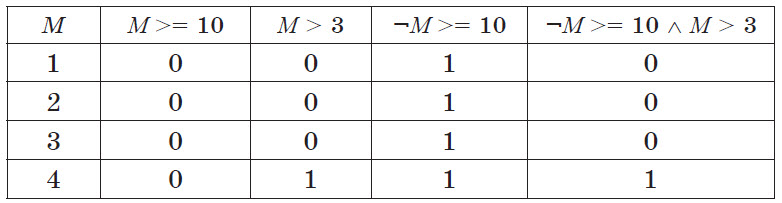
Последний столбец содержит результат всего выражения. Истинным оно будет только для значения числа М, равного 4.
Ответ: 4) 4.

Пример 7.
В табличной форме представлены ежемесячные данные о продаже групп товаров за полгода. Сколько групп товаров демонстрировали рост продаж в весенние месяцы или вышли на уровень свыше 80 % в июне?

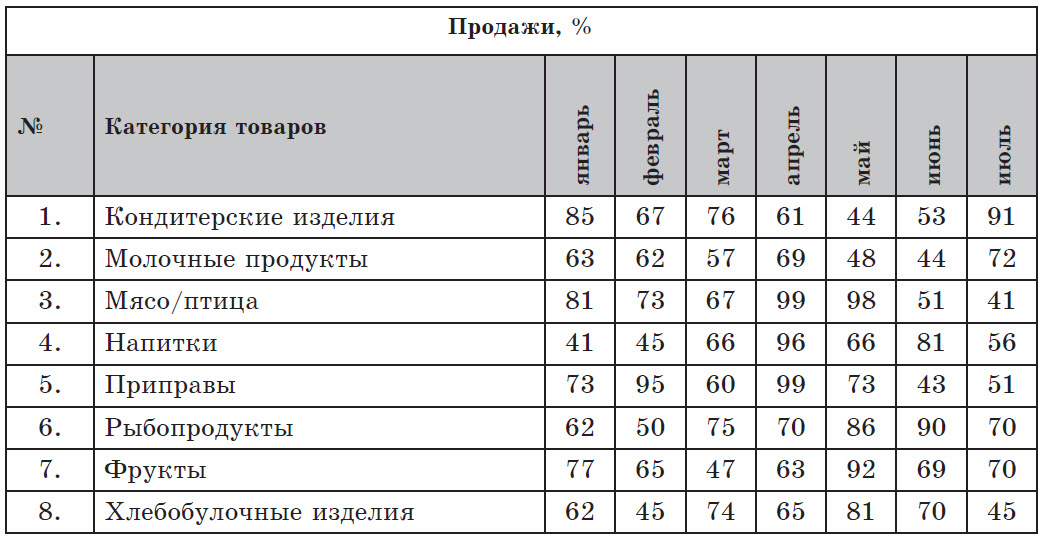
Решение. Переформулируем условие задачи: необходимо найти группы товаров, для которых (Март < Апрель) ∧ (Апрель < Май) v (Июнь > 80).

Введем обозначения:
А = (Март < Апрель)
В = (Апрель < Май)
С = (Июнь > 80)

Тогда выражение можно записать как А ∧ В v С.

Логическое выражение состоит из одной конъюнкции и одной дизъюнкции. Значение выражения конъюнкции истинно только тогда, когда истинны оба составляющие его простых выражения ((Март < Апрель) и (Апрель < Май)). Значение выражения дизъюнкции будет истинным, если хотя бы одно из составляющих его простых высказываний будет истинным.

Составим таблицу истинности для исходных данных.

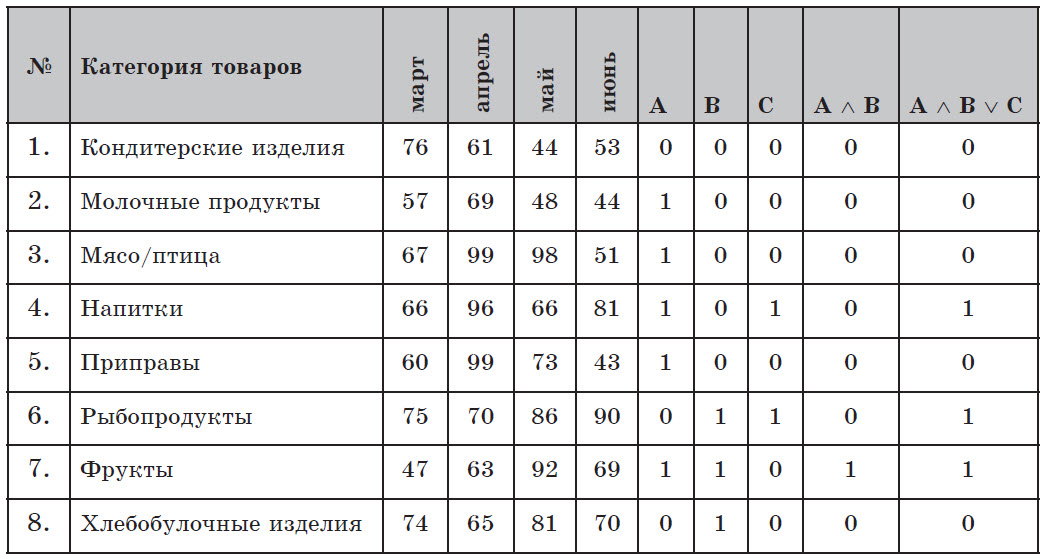
Логическому выражению удовлетворяют 3 записи — 4–я, 6–я и 7–я.
Ответ: 3.

 

---

Конспект урока по информатике «Логические значения, операции, выражения».

Вернуться к Списку конспектов по информатике.