|
Учебный курс «Информатика»
 Триггер
Триггер
Логика очень древняя наука. Ещё в античные времена была известна формальная логика, позволяющая делать заключения о правильности какого-либо суждения не по его фактическому содержанию, а только по форме его построения. Например, уже в древности был известен закон исключения третьего. Его содержательная трактовка была такова: «Во время своих странствований Платон был в Египте ИЛИ не был Платон в Египте». В такой форме это или любое другое выражение будут правильны (тогда говорили: истинно). Ничего другого быть не может: Платон либо был, либо не был в Египте — третьего не дано.
 Если из теории следуют два противоречащих друг другу вывода, то такая теория безусловно неправильная (ложная) и должна быть отвергнута.
Если из теории следуют два противоречащих друг другу вывода, то такая теория безусловно неправильная (ложная) и должна быть отвергнута.
Формальная логика основана на “высказываниях”. “Высказывание” — это основной элемент логики, определяемый как повествовательное предложение, относительно которого можно однозначно сказать, истинное или ложное утверждение оно содержит.
Например: Листва на деревьях опадает осенью. Земля прямоугольная.
Первое высказывание содержит истинную информацию, а второе — ложную. Вопросительное, побудительное и восклицательное предложения не являются высказываниями, так как в них ничего не утверждается и не отрицается.
Высказывания могут быть и такими: 2>1, Н2О+SO3=h3SO4.
 Здесь используются языки математических символов и химических формул.
Здесь используются языки математических символов и химических формул.
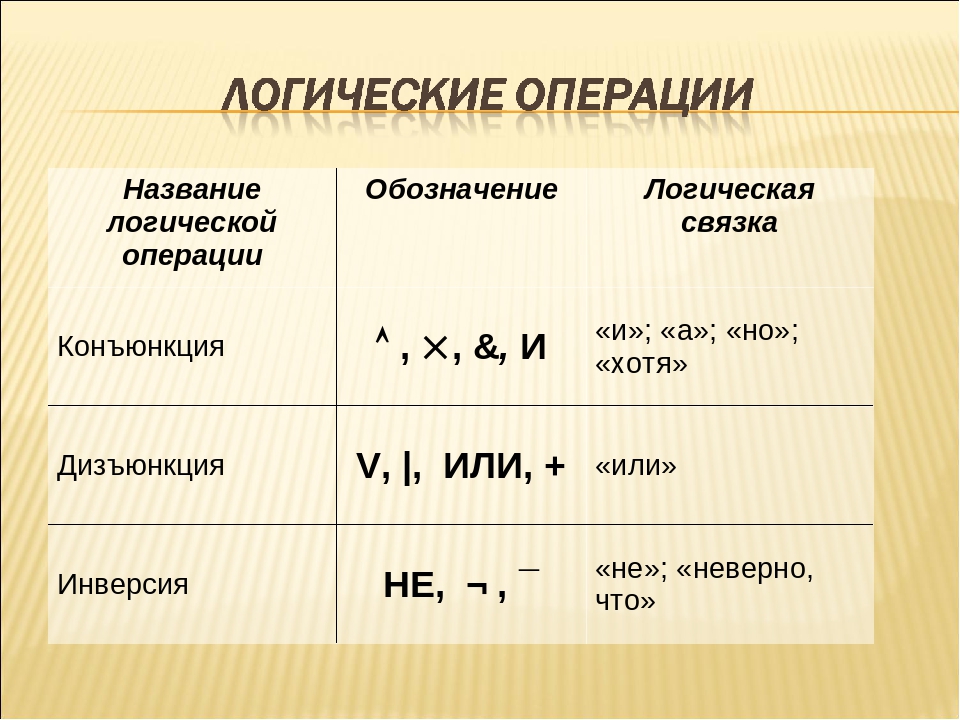
Приведённые выше примеры высказываний являются простыми. Но из простых высказываний можно получить сложные, объединив их с помощью логических связок. Логические связки — это слова, которые подразумевают определённые логические связи между высказываниями. Основные логические связки издавна употребляются не только в научном языке, но и в обыденном, — это “и”, “или”, “не”, “если … то”, “либо … либо” и другие известные нам из русского языка связки. В рассмотренных нами трёх законах формальной логики использовались связки “и”, “или”, “не”, “если … то” для связи простых высказываний в сложные.
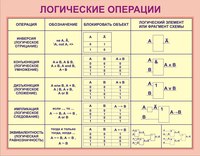
Формальная логика была известна в средневековой Европе, она развивалась и обогащалась новыми законами и правилами, но при этом вплоть до 19 века она оставалась обобщением конкретных содержательных данных и её законы сохраняли форму высказываний на разговорном языке.
В 1847 году английский математик Джордж Буль, преподаватель провинциального университета в маленьком городке Корке на юге Англии разработал алгебру логики.
Алгебра логики очень проста, так как каждая переменная может принимать только два значения: истинно или ложно. Трудность изучения алгебры логики возникает из-за того, что для обозначения переменных принимают символы 0 и 1, которые по написанию совпадают с обычными арифметическими единицей и нулём. Но совпадение это только внешнее, так как смысл они имеют совсем иной.
 е. ложно. Высказывание заменилось на логическое выражение, которое строится из логических переменных (А, В, Х, …) и логических операций (связок).
е. ложно. Высказывание заменилось на логическое выражение, которое строится из логических переменных (А, В, Х, …) и логических операций (связок).
В алгебре логики знаки операций обозначают лишь три логические связки
1.Логическая операция ИЛИ. Логическую функцию принято задавать в виде таблицы. В левой части этой таблицы перечисляются все возможные значения аргументов функции, т.е. входные величины, а в правой указывается соответствующее им значение логической функции. Для элементарных функций получается таблица истинности данной логической операции. Для операции ИЛИ таблица истинности имеет вид:
Операцию ИЛИ называют также логическим сложением, и потому её можно обозначать знаком «+».
Рассмотрим сложное единичное высказывание: «Летом я поеду в деревню или в туристическую поездку». Обозначим через
 Тогда логическое выражение сложного высказывания имеет вид А+В, и оно будет ложным только, если ни одно из простых высказываний не будет истинным.
Тогда логическое выражение сложного высказывания имеет вид А+В, и оно будет ложным только, если ни одно из простых высказываний не будет истинным.
2. Логическая операция И. Таблица истинности для этой функции имеет вид:
Из таблицы истинности следует, что операция И — это логическое умножение, которое ничем не отличается от традиционно известного умножения в обычной алгебре. Операцию И можно обозначить знаком по-разному:
В формальной логике операции логического умножения соответствуют связки и, а, но, хотя.
3. Логическая операция НЕ. Эта операция является специфичной для алгебры логики и не имеет аналога в обычной алгебре. Она обозначается чертой над значением переменной, либо знаком приставки перед значением переменной:
Читается в обоих случаях одинаково «Не А». Таблица истинности для этой функции имеет вид:
В вычислительной технике операцию НЕ называют отрицанием или инверсией, операцию ИЛИ — дизъюнкцией, операцию И — конъюнкцией. Набор логических функций “И”, “ИЛИ”, “НЕ” является функционально полным набором или базисом алгебры логики. С помощью него можно выразить любые другие логические функции, например операции “строгой дизъюнкции”, “импликации” и “эквивалентности” и др. Рассмотрим некоторые из них.
Набор логических функций “И”, “ИЛИ”, “НЕ” является функционально полным набором или базисом алгебры логики. С помощью него можно выразить любые другие логические функции, например операции “строгой дизъюнкции”, “импликации” и “эквивалентности” и др. Рассмотрим некоторые из них.
Логическая операция “строгая дизъюнкция”. Этой логической операции соответствует логическая связка “либо … либо”. Таблица истинности для этой функции имеет вид:
Операция “строгая дизъюнкция” выражается через логические функции “И”, “ИЛИ”, “НЕ” любой из двух логических формул:
и иначе называется операцией неравнозначности или “сложения по модулю 2”, так как при сложении чётного количества единиц, результатом будет “0”, а при сложении нечётного числа единиц, результат станет равен “1”.
Логическая операция “импликация”. Выражение, начинающееся со слов если, когда, коль скоро и продолжающееся словами то, тогда, называется условным высказыванием или операцией «импликация». Таблица истинности для этой функции имеет вид:
Таблица истинности для этой функции имеет вид:
Операцию “импликация” можно обозначить по-разному:
Эти выражения эквивалентны и читаются одинаково: «Игрек равен импликации от А и В». Операция “импликация” выражается через логические функции “ИЛИ”, “НЕ” в виде логической формулы
Логическая операция “эквивалентность” (равнозначность). Этой логической операции соответствуют логические связки “если и только если”, «тогда и только тогда, когда». Таблица истинности для этой функции имеет вид:
Операция “эквивалентность” обозначается по-разному. Выражения
обозначают одно и тоже, и можно сказать, что А эквивалентна В, если и только если они равнозначны. Логическая операция “эквивалентность” выражается через логические функции “И”, “ИЛИ”, “НЕ” в виде логической формулы
С помощью алгебры логики можно очень кратко записать законы формальной логики и дать им математически строгое доказательство.
В алгебре логики, как в элементарной, справедливы переместительный (закон коммутативности), сочетательный (закон ассоциативности) и распределительный (закон дистрибутивности) законы, а также аксиома идемпотентности (отсутствие степеней и коэффициэнтов) и др., в записях которых используются логические переменные, принимающие только два значения — логический ноль и логическая единица. Применение этих законов позволяет производить упрощение логических функций, т.е. находить для них выражения, имеющие наиболее простую форму. Основные аксиомы и законы алгебры логики приведены в таблице:
Примеры использования основных аксиом и законов:| Обозначение | Наименование документа | Файл PDF | ||
| РД ПГУТИ 2.01.7-2016 | Управление организации учебного процесса. Положение | |||
РД ПГУТИ 2.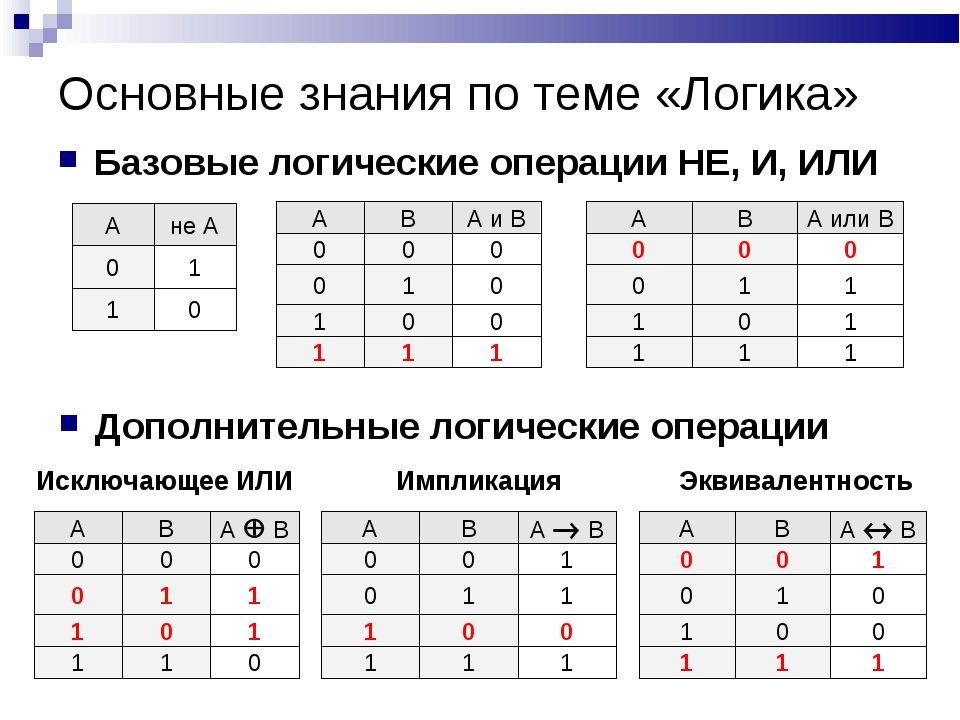 02.7-2016 02.7-2016 | Отдел учебных лабораторий. Положение | |||
| РД ПГУТИ 2.03.7-2017 | Организация образовательной деятельности по заочной форме обучения с применением дистанционных технологий в ПГУТИ. Положение | |||
| РД ПГУТИ 2.04.7-2017 | Порядок организации и осуществления образовательной деятельности по образовательным программам высшего образования. Положение | скачать | ||
| РД ПГУТИ 2.05.7-2020 | Порядок применения электронного обучения, дистанционных образовательных технологий при реализации образовательных программ в ПГУТИ. Положение | скачать | ||
| РД ПГУТИ 2.06.6-2019 | Кафедра университета. Положение | |||
| РД ПГУТИ 2.08.6-2020 | Факультет университета. Положение | |||
| РД ПГУТИ 2.10.4-2017 | Учебно-методический комплекс. Положение | |||
| РД ПГУТИ 2.11.7-2020 | Организация и проведение курсового проектирования. Положение Положение | |||
РД ПГУТИ 2.13.7-2017 | Порядок заполнения, учета и выдачи документов о высшем образовании и о квалификации и их дубликатов. Положение | |||
РД ПГУТИ 2.14.7-2021 | Подготовка магистров в ПГУТИ. Положение | |||
| РД ПГУТИ 2.15.7 — 2016 | Порядок проведения нормоконтроля в ПГУТИ. Положение | |||
| РД ПГУТИ 2.16.7 — 2021 | Порядок проверки выпускных квалификационных работ обучающихся по программам бакалавриата, специалитета и магистратуры и аспирантуры на плагиат в ПГУТИ. Положение | скачать | ||
| РД ПГУТИ 2.18.7 — 2021 | Выпускные квалификационные работы. Порядок подготовки, оформления и защиты. Положение | |||
| РД ПГУТИ 2.22.7-2017 | Практики учебные и производственные. Общие требования к организации и проведению. Положение | |||
РД ПГУТИ 2.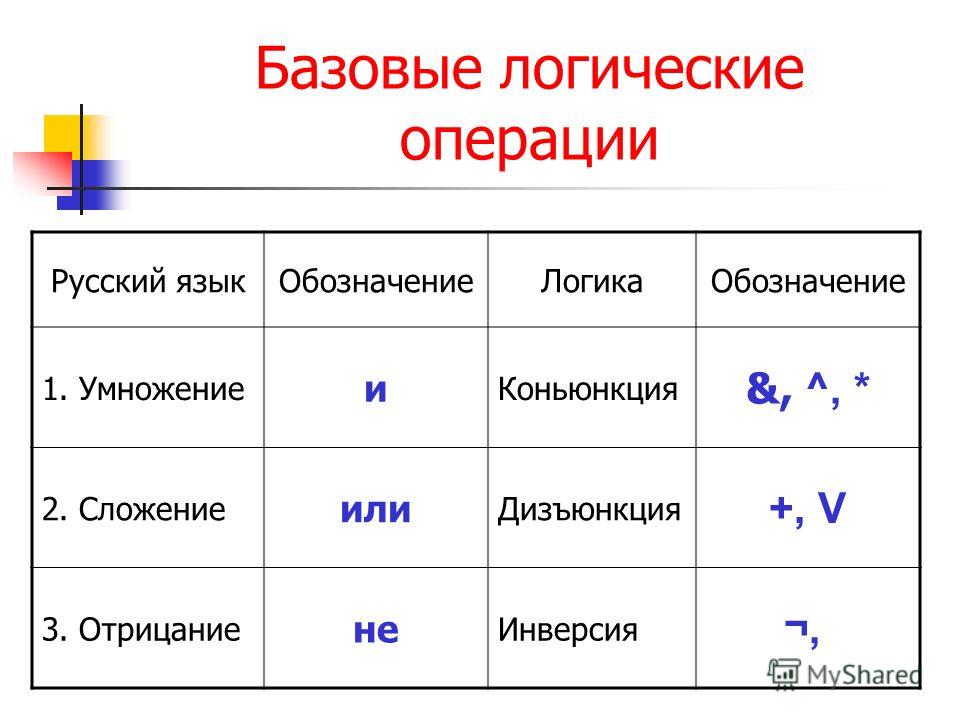 22.7-2020 22.7-2020 | Практики учебные и производственные. Общие требования к организации и проведению. Положение | |||
| РД ПГУТИ 2.23.7-2009 | Компьютерное тестирование. Правила | |||
| РД ПГУТИ 2.25.7-2019 | Отдел магистратуры. Положение | скачать | ||
| РД ПГУТИ 2.26.7-2021 | Магистерская диссертация. Порядок подготовки, оформления и защиты. Положение | |||
| РД ПГУТИ 2.28.7-2017 | Основная образовательная программа. Программа формирования. Общие требования. | |||
| РД ПГУТИ 2.28.7-2018 | Основная профессиональная образовательная программа. Программа формирования. Общие требования. | |||
| РД ПГУТИ 2.30.7-2017 | Рабочая программа дисциплины. Общие требования. С изм. и доп. | |||
| РД ПГУТИ 2.30.7-2018 | Рабочая программа дисциплины. Общие требования Общие требования | |||
| РД ПГУТИ 2.31.7-2017 | Фонд оценочных средств для текущей, промежуточной и государственной итоговой аттестации студентов в ПГУТИ. Положение с изм. и доп. | скачать | ||
| РД ПГУТИ 2.31.7-2018 | Оценочные средства для текущей, промежуточной и государственной итоговой аттестации студентов в ПГУТИ. Положение | |||
| РД ПГУТИ 2.32.7-2020 | Организация и проведение лабораторных занятий. Положение | |||
| РД ПГУТИ 2.33.7-2020 | Организация и проведение практических занятий. Положение | |||
| РД ПГУТИ 2.34.7-2020 | Организация и проведение лекционных занятий. Положение | скачать | ||
| РД ПГУТИ 2.35.7-2020 | Рейтинговая оценка деятельности педагогических работников, относящихся к профессорско-преподавательскому сотаву. Положение | скачать | ||
| РД ПГУТИ 2.36.7-2011 | Учебная лаборатория кафедры. Положение Положение | |||
| РД ПГУТИ 2.40.4-2015 | Правила оформления учебных изданий ПГУТИ. Положение | |||
| РД ПГУТИ 2.45.7-2016 | Правила оформления текстовых студенческих работ в ПГУТИ. Положение | |||
| РД ПГУТИ 2.47.7-2017 | Порядок организации контактной работы обучающихся с преподавателем в процессе освоения образовательной программы высшего образования. Положение | |||
| РД ПГУТИ 2.50.6-2016 | Научно-техническая библиотека. Положение | |||
| РД ПГУТИ 2.54.6-2017 | Выпускающая кафедра. Положение | |||
| РД ПГУТИ 2.53.6-2016 | Базовая кафедра. Положение | |||
| РД ПГУТИ 2.57.6-2015 | Порядок участия обучающихся в формировании содержания своего профессионального образования. Положение | |||
| РД ПГУТИ 2.61.7-2017 | Текущий контроль успеваемости студентов и промежуточная аттестация. Положение Положение | |||
| РД ПГУТИ 2.62.7-2017 | Государственная итоговая аттестация. Положение | |||
| РД ПГУТИ 2.62.7-2020 | Государственная итоговая аттестация. Положение | |||
| РД ПГУТИ 2.63.7-2017 | Программа государственной итоговой аттестации. Положение | |||
| РД ПГУТИ 2.63.7-2018 | Программа государственной итоговой аттестации. Положение | |||
| РД ПГУТИ 2.64.7-2017 | Порядок перевода, отчисления и востановления студентов в ПГУТИ. Положение | |||
| РД ПГУТИ 2.67.7-2015 | Порядок предоставления академического отпуска лицам, обучающимся по образовательным программам высшего образования в ПГУТИ. Положение | |||
| РД ПГУТИ 2.69.7-2021 | Особенности проведения государственных аттестационных испытаний с применением электронного обучения, дистанционных образовательных технологий в ПГУТИ. Положение Положение | скачать | ||
| РД ПГУТИ 2.73.7-2017 | Порядок обучения по индивидуальному учебному плану в ПГУТИ. Положение | |||
| РД ПГУТИ 2.76.7-2020 | Организация самостоятельной работы студентов в ПГУТИ. Положение | |||
| РД ПГУТИ 2.77.7-2017 | Порядок формирования и освоения элективных и факультативных дисциплин в ПГУТИ. Положение | |||
| РД ПГУТИ 2.79.7-2017 | Реализация дисциплины «Физическая культура и спорт». Положение | |||
| РД ПГУТИ 2.80.7-2011 | Процедура выдачи европейского приложения к диплому. Общие требования | |||
| РД ПГУТИ 2.82.7-2016 | Порядок заполнения и выдачи справок об обучениии. Положение | |||
| РД ПГУТИ 2.83.7-2017 | Порядок организации сетевых форм реализации образовательных программ в ПГУТИ. Положение | |||
| РД ПГУТИ 2.84.7-2017 | Сетевая форма реализации образовательных программ магистратуры в ПГУТИ. Положение Положение | |||
| РД ПГУТИ 2.85.6-2019 | Портфолио обучающегося в ПГУТИ. Положение | |||
| РД ПГУТИ 2.87.6-2015 | Академические права и обязанности обучающихся в ПГУТИ. Положение | |||
| РД ПГУТИ 2.88.7-2017 | Организация обучения студентов-инвалидов и студентов с ограниченными возможностями здоровья в ПГУТИ. Положение |
| Наименование | Обозначение | Функция |
| Блок начало-конец(пуск-остановка) | Элементотображает вход из внешней среды или выход из неё (наиболее частое применение? начало и конец программы). Внутри фигуры записывается соответствующеедействие. | |
| Блок вычислений (вычислительный блок) | Выполнениеодной или нескольких операций, обработка данных любого вида (изменениезначения данных, формы представления, расположения). Внутри фигуры записываютнепосредственно сами операции, например, операцию присваивания: a = 10*b + c. Внутри фигуры записываютнепосредственно сами операции, например, операцию присваивания: a = 10*b + c. | |
| Логический блок (блок условия) | Отображаетрешение или функцию переключательного типа с одним входом и двумя или болееальтернативными выходами, из которых только один может быть выбран послевычисления условий, определенных внутри этого элемента. Вход в элементобозначается линией, входящей обычно в верхнюю вершину элемента. Если выходовдва или три, то обычно каждый выход обозначается линией, выходящей изоставшихся вершин (боковых и нижней). Если выходов больше трех, то их следуетпоказывать одной линией, выходящей из вершины (чаще нижней) элемента, котораязатем разветвляется. Соответствующие результаты вычислений могут записыватьсярядом с линиями, отображающими эти пути. Примеры решения: в общем случае? сравнение (три выхода: , | |
| Предопределённый процесс | Символотображает выполнение процесса, состоящего из одной или нескольких операций,который определен в другом месте программы (в подпрограмме, модуле). Внутрисимвола записывается название процесса и передаваемые в него данные.Например, в программировании ? вызов процедуры или функции. Внутрисимвола записывается название процесса и передаваемые в него данные.Например, в программировании ? вызов процедуры или функции. | |
| Данные(ввод-вывод) | Преобразованиеданных в форму, пригодную для обработки (ввод) или отображения результатовобработки (вывод). Данный символ не определяет носителя данных (для указаниятипа носителя данных используются специфические символы). | |
| Граница цикла | Символсостоит из двух частей ? соответственно, начало и конец цикла ?операции, выполняемые внутри цикла, размещаются между ними. Условия цикла иприращения записываются внутри символа начала или конца цикла ? взависимости от типа организации цикла. Часто для изображения на блок-схемецикла вместо данного символа используют символ условия, указывая в нёмрешение, а одну из линий выхода замыкают выше в блок-схеме (перед операциямицикла). | |
| Соединитель | Символотображает вход в часть схемы и выход из другой части этой схемы. Используется для обрыва линии и продолжения её в другом месте (для избежанияизлишних пересечений или слишком длинных линий, а также, если схема состоитиз нескольких страниц). Соответствующие соединительные символы должны иметьодинаковое (при том уникальное) обозначение. Используется для обрыва линии и продолжения её в другом месте (для избежанияизлишних пересечений или слишком длинных линий, а также, если схема состоитиз нескольких страниц). Соответствующие соединительные символы должны иметьодинаковое (при том уникальное) обозначение. | |
| Комментарий | Используетсядля более подробного описания шага, процесса или группы процессов. Описаниепомещается со стороны квадратной скобки и охватывается ей по всей высоте.Пунктирная линия идет к описываемому элементу, либо группе элементов (приэтом группа выделяется замкнутой пунктирной линией). Также символ комментарияследует использовать в тех случаях, когда объём текста, помещаемого внутринекоего символа (например, символ процесса, символ данных и др.), превышаетразмер самого этого символа. |
: Электронное правительство :: Управление информационно- коммуникационных технологий и связи :: Структурные подразделения администрации :: Администрация :: Krd.ru
- Глобальная сеть, в которую входят правительственные, академические, коммерческие, военные и корпоративные сети всего мира, в основе которой лежит использование протокола передачи данных IP (Inter-network Protocol).
- Глобальная информационная система, части которой логически взаимосвязаны друг с другом посредством уникального адресного пространства, основанного на протоколе IP, и которая обеспечивает, публично или частным образом, коммуникационный сервис высокого уровня.
- Множество взаимосвязанных компьютерных сетей, окутывающих земной шар. Интернет обеспечивает доступ к компьютерам, электронной почте, доскам объявлений, базам данных и дискуссионным группам, все из которых используют протокол IP.
Всемирная информационная компьютерная сеть Интернет представляет собой объединение множества региональных компьютерных сетей и компьютеров, обменивающихся друг с другом информацией по каналам общественных телекоммуникаций (телефонной, радио и спутниковой связи). И. появился в конце 70-х — начале 80-х годов в результате постепенного объединения с помощью средств телекоммуникаций, компьютерной сети Министерства обороны США, сети Национального научного фонда правительства США, региональных и даже локальных вычислительных сетей. Согласно официальным данным, в период с 1989 по 1995 гг. сеть И. росла, ежегодно удваивая свои размеры. В настоящее время сеть перешла на коммерческую основу, однако формально ее контролирует общественная организация ISOC (Internet SOCiety). Входящие в И. компьютерные сети взаимодействуют с помощью протоколов IP, которые позволяют связывать между собой компьютеры различной архитектуры, производимые разными фирмами. Под словом И. обычно подразумевают физический уровень сети, т. е. аппаратное обеспечение, состоящее из компьютеров, кабелей и других устройств передачи данных. Работу в И. обеспечивают базовые программные средства. Они осуществляют поиск нужной информации в архивах, размещенных внутри И., перемещают файлы из компьютера в компьютер, обеспечивают вход в другие компьютеры, доступ к множеству серверов и баз данных. С помощью аппаратных и программных средств И. предоставляет пользователю различные информационные услуги, среди которых электронная почта, службы электронных объявлений, телеконференций и рекламы. С начала 90-х годов в И. существует сервис, называемый Всемирной паутиной (World Wide Web). Технология World Wide Web позволяет на основе гипертекста и гипермедиа создавать и хранить информацию в форме документов Web и просматривать все документы Web, хранящиеся в компьютерах глобальной сети, через систему связывающих их ссылок. Подключить компьютер к И. и стать пользователем электронной почты, Всемирной паутины и других услуг И. помогают поставщики сетевых услуг (провайдеры).
Логарифмы в информатике для обозначения Big O?
Когда вы вычисляете нотацию Big O, вы вычисляете сложность алгоритма по мере увеличения размера задачи.
Например, при выполнении линейного поиска по списку наихудшим возможным случаем является то, что элемент либо находится в последнем индексе, либо вообще отсутствует в списке, что означает, что ваш поиск будет выполнять N шагов, причем N-это количество элементов в списке. O(N).
Алгоритм, который всегда будет выполнять одинаковое количество шагов, независимо от размера проблемы, — это O(1).
Логарифмы вступают в игру, когда вы сокращаете размер задачи по мере прохождения алгоритма. Для BST вы начинаете с середины списка. Если элемент для поиска меньше, вы фокусируетесь только на первой половине списка. Если он больше, вы фокусируетесь только на второй половине. Сделав всего один шаг, вы просто сократите размер вашей проблемы вдвое. Вы продолжаете разрезать список пополам, пока не найдете элемент или не сможете продолжить. (Обратите внимание, что двоичный поиск предполагает, что список находится в порядке)
Давайте рассмотрим, что мы ищем 0 в приведенном ниже списке (BST представлен в виде упорядоченного списка): [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]
Сначала мы начинаем с середины: 7 0 меньше 7, поэтому мы смотрим в первой половине списка: [0,1,2,3,4,5,6]
Мы смотрим в середину этого списка: 3 0 меньше 3, и наш рабочий список теперь: [0,1,2]
Итак, мы смотрим на 1. 0 меньше 1, поэтому наш список теперь [0].
Учитывая, что у нас есть рабочий список всего из 1 элемента, мы находимся в худшем случае.5 = 32 ИЛИ логарифмическая база 2 из 32 равна 5).
Поэтому Big O для a BST равно O(logN) (обратите внимание, что мы используем основание 2 для логарифмов в CS).
Для O(NlogN) наихудшим случаем является размер проблемы, умноженный на вычисление ее логарифма. Сортировка вставки, быстрая сортировка и сортировка слиянием-все это примеры O(NlogN)
Уважаемые коллеги! Мы рады приветствовать вас в авторской мастерской А.В. Горячева и Д.И. Павлова, посвящённой УМК «Информатика для всех». Уверены, вы найдёте для себя полезную информацию. Если же у Вас останутся вопросы — вы можете связаться с нами. С уважением, А.В. Горячев, Д.И. Павлов Разработка УМК «Информатика для всех» велась 5 лет, с момента внедрения ФГОС НОО. Предпосылкой к разработке стал изменившийся характер начального курса информатики. Анализ ФГОС НОО показывает, что требования к освоению информационной грамотности сегодня отнесены не только к предметной области «Математика и информатика», но и к ряду других предметных областей. Кроме того, ожидаемые метапредметные результаты освоения программы начальной школы, являющиеся универсальными для всех дисциплин, во многом лежат в предметном поле информатики как науки и как учебной дисциплины. Предложенная концепция курса расширяет ставшую традиционной систему представлений о информатике в начальной школе. Помимо стандартных направлений «Алгоритмизация, формализация, логика» в программу добавлены элементы социальной информатики. Большое внимание уделяется навыкам «ПОЛУЧЕНИЯ» и «ПЕРЕДАЧИ» информации, работе с таблицами, изображениями, диаграммами, графами, инфографикой и другими формами представления информации. В работе над УМК учитывались пожелания педагогов, апробировавших отдельные элементы курса и весь курс целиком. Это позволило сформировать такую модель обучения, которая отражает метапредметный характер информатики и позволяет оснастить учеников необходимыми знаниями и умениями, которые позволяют им легче и качественнее решать информационные задачи, задачи учебного, творческого и познавательного характера. И конечно же выполнять проверочные работы, в том числе метапредметные тесты и аттестационные задания. |
— Ищу словарь математических / CS-обозначений
Иногда в статьях по математике и информатике используется ошеломляющий набор символов. Тем не менее, многие предполагают базовое знакомство, которому, кажется, редко учат в одном месте. Я ищу словарь примерно следующего содержания, особенно с точки зрения CS.
- В нем будут перечислены все основные математические символы, даны их значения и примеры. Это будет говорить о символах, которые иногда используются аналогичным образом.Было бы замечено типичные ошибки новичков.
- Он говорил бы о тонкостях, связанных с различными значениями одного символа (так же, как несколько определений одного и того же слова в словаре).
- Это не было бы просто очень кратким описанием каждого символа, например однословными описаниями, такими как «подмножество».
- Это показало бы, как символы иногда «перегружаются». Например, $ \ binom {x} {y} $ может иметь $ z $ как целое число, но иногда $ z $ может быть набором с этой нотацией, что означает выбор элементов из этого набора.$ [n] $ иногда означает набор целых чисел $ 1 \ ldots n $, а иногда — одноэлементный массив.
- Он может говорить о том, как описывать все виды различных «объектов» в терминах различных символов или эквивалентных способов обращения к ним (но которые более понятны) и о возможных операциях с этими объектами. Другими словами, что-то вроде API для математических объектов.
Т.е. временами это могло бы быть также «руководство по стилю» для различных нюансов в том, как представить математическое письмо.Это был бы очень полезный ресурс для тех, кто пишет вопросы в математических обменах стеками, где многие вопросы не имеют смысла из-за того, что не укладываются в сложные математические соглашения.
Некоторые вводные книги содержат многие из этих функций. однако в идеале это было бы отдельное лечение. Кроме того, в идеале, конечно, это было бы онлайн. Есть таблицы латексных символов, но они не соответствуют многим из вышеперечисленных критериев.
Кто-нибудь видел «словарь символов», соответствующий этим характеристикам?
(В качестве альтернативы, это может показаться отличным проектом вики или FAQ, если таких хороших ссылок не существует.)
Обозначение стрелки? — Обмен стеков информатики
Вообще стандартов на псевдокод нет. Каждый может создать свой собственный псевдокод, как ему заблагорассудится. Обычно автор должен определить соглашения, которые он использует для своего псевдокода.
К сожалению, псевдокод часто используется без его документирования, исходя из предположения, что читателю будет «очевидно», что означает этот код. Как вы обнаружили, то, что очевидно, а что нет, очевидно, зависит от читателя!
В моем случае опубликованный вами фрагмент очевиден для меня, потому что я привык к языкам программирования, которые одинаково используют символ оператора ← : Scala, Haskell, исторический Smalltalk.
Стрелки обычно используются для обозначения того, что «что-то» «течет» в направлении стрелки. Стрелка вправо обычно означает «переходит к» в смысле отображения или функции. Стрелка влево обычно означает «становится», «позволяет» или «берет из». Однако стрелки также могут указывать на отправку или получение сообщений. Вы должны осознавать контекст.
Этот код выглядит как простой императивный структурированный программный код, поэтому значение «присваивания» является более вероятной интерпретацией, но если это псевдокод для некоторого вычисления процесса, асинхронный, параллельный, параллельный или распределенный алгоритм или структура данных или что-то в этом роде, вероятно, это также может означать «блоки до получения сообщения» или что-то в этом роде.
В данном конкретном случае две стрелки влево имеют немного разные, но тесно связанные значения:
Второй просто означает « Legal становится True », так что это форма назначения. (Этот синтаксис присваивания фактически использовался историческими версиями Smalltalk.)
Первый также означает присвоение, но интерпретируется как то, что j принимает все значения с правой стороны, одно за другим.Другими словами, это цикл итератора FOREACH . (На самом деле Scala использует стрелку влево именно в этом значении в своем для понимания .)
Обозначение Big-O, объясненное программистом-самоучкой
Это первый из трех постов. Во втором посте говорится о как рассчитать Big-O. В третьей статье говорится о понимании формальное определение Big-O.
Обозначение Big-O было для меня действительно пугающим понятием.я думал так «настоящие» программисты говорили о своем коде. Это было все страшнее, потому что академические описания (например, Википедия) сделали для меня очень мало смысла. Это расстраивает, потому что лежащие в основе концепции на самом деле не так уж и сложны.
Проще говоря, нотация Big-O — это то, как программисты говорят о алгоритмы. Алгоритмы — еще одна страшная тема, о которой я расскажу в другой пост, но для наших целей допустим, что «алгоритм» означает функции в вашей программе (что не так уж и далеко).Big-O функции обозначение определяется тем, как он реагирует на различные входные данные. Как намного медленнее, если мы дадим ему список из 1000 вещей, над которыми нужно работать вместо списка по 1 штуке?
Рассмотрим этот код:
def item_in_list (to_check, the_list):
для элемента в the_list:
если to_check == item:
вернуть True
вернуть ложь
Поэтому, если мы вызовем эту функцию как item_in_list (2, [1,2,3]) , она должна
будь довольно быстрым. Мы перебираем каждую вещь в списке, и если мы находим
первый аргумент нашей функции, верните True.Если мы дойдем до конца
и мы его не нашли, верните False.
«Сложность» этой функции — O (n) . Я объясню что это
означает всего за секунду, но давайте разберемся с этим математическим
синтаксис. O (n) читается как «Порядок N», потому что функция O также
известная как функция заказа. Я думаю, это потому, что мы делаем
приближение, которое имеет дело с «порядками величины».
«Порядки величин» — это , ЕЩЕ ДРУГОЙ математический термин, который в основном говорит о разнице между классами чисел.Подумайте о разница между 10 и 100. Если вы изобразите 10 ближайших друзья и 100 человек, это действительно большая разница. Аналогичным образом разница между 1000 и 10000 довольно велика (на самом деле, это разница между юнкерской машиной и мало подержанной). Оказывается что в приближении, если вы на порядок, ты довольно близок. Если бы вы угадали количество жевательных резинок в машина, вы были бы в пределах порядка, если бы сказали 200 жевательные резинки. 10 000 гамболов будут отключены от WAY и .
Рис. 1. Аппарат для жевательной резинки с количеством жевательных шариков, вероятно, в пределах порядка 200.
Вернемся к анализу O (n) , это говорит о том, что если бы мы построили график времени
требуется для запуска этой функции с входами разного размера (например,
массив из 1 элемента, 2 элемента, 3 элемента и т. д.), мы увидим, что он
примерно соответствует количеству элементов в массиве. Это
называется линейным графом. Это означает, что линия в основном прямая.
если бы вы изобразили это.
Некоторые из вас могли заметить это, если в приведенном выше примере кода наш item всегда был первым элементом в списке, наш код действительно был бы быстрый! Это правда, но Big-O — это приблизительный наихудший случай. выполнение чего-либо. Наихудший случай для приведенного выше кода: что то, что мы ищем, вообще нет в списке. (Примечание: Математический термин для этого — «верхняя граница», что означает, что речь идет о математический предел ужаса).
Если вы хотите увидеть график для этих функций, игнорируйте O () функцию и замените переменную n на x .Затем вы можете ввести это
в Wolfram Alpha как «график x», который покажет вам диагональ
линия. Причина, по которой вы заменяете n на x, заключается в том, что их графическая программа
хочет x в качестве имени переменной, потому что это соответствует x
ось. Ось x, увеличивающаяся слева направо, соответствует
предоставление вашей функции все больших и больших массивов. Ось Y
представляет время, поэтому чем выше линия, тем она медленнее.
Рисунок 2: Характеристики времени выполнения функции O (n)
Итак, каковы еще примеры этого?
Рассмотрим эту функцию:
def is_none (элемент):
возврат товара нет
Это немного глупый пример, но потерпите меня.Эта функция
называется O (1) , что называется «постоянное время». Это значит, что нет
независимо от того, насколько велик наш вклад, он всегда занимает одинаковое количество времени
вычислять вещи. Если вы вернетесь к Wolfram и plot 1 , вы увидите
что он всегда остается неизменным, независимо от того, как далеко мы идем. если ты
передать список из 1 миллиона целых чисел, это займет примерно столько же времени
как если бы вы собирались передать список из 1 целого числа. Постоянное время
считается лучшим сценарием для функции.
Рисунок 3: Характеристики времени выполнения функции O (1)
Рассмотрим эту функцию:
def all_combinations (the_list):
результаты = []
для элемента в the_list:
для inner_item в the_list:
results.append ((элемент, внутренний_элемент))
вернуть результаты
Это сопоставляет каждый элемент в списке с каждым другим элементом в
список. Если бы мы дали ему массив [1,2,3] , мы бы вернулись [(1,1) (1,2),
(1,3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)] .2) Функция будет очень быстро замедляться, если
то, что работает в постоянное время, будет намного лучше. Это
особенно полезно, когда речь идет о структурах данных, которые я опубликую
о скоро.
Рисунок 4: Сравнение функций O (n 2 ), O (n) и O (1)
Это довольно подробный обзор нотации Big-O, но, надеюсь, знакомит с темой. Есть курс Coursera, который может дать вам более подробное представление об этой теме, но имейте в виду, что он очень быстро перейдет в математическую нотацию.Если что-нибудь здесь не имеет смысла, напишите мне по электронной почте.
Обновление : я также писал о том, как вычислить Big-O.
Думаю написать книгу на эту тему. Если это что-то вы хотели бы видеть, пожалуйста, выразите свой интерес здесь.
Какое значение математики в компьютерных науках?
Математика была проклятием для многих студентов (включая мою !!!) с самого начала. С другой стороны, Computer Science довольно интересен, и студенты изучают его в надежде стать следующим вундеркиндом в программировании !!! Но подождите… неужели это так просто? !! Нет, друзья мои, это не….На самом деле компьютерные науки очень тесно связаны с математикой.
В течение многих лет было много споров о важности математики в компьютерных науках. Некоторые считают, что это мало что значит для компьютерных наук, в то время как другие (в большинстве своем!) Считают, что это фундамент, на котором построены компьютерные науки. По данным Оксфордского университета:
Математика — это фундаментальный интеллектуальный инструмент в вычислениях, но вычисления также все чаще используются в качестве ключевого компонента при решении математических задач.
Даже если математика имеет такую ценность … остается вопрос: « Почему математика так важна в информатике? ”Итак, давайте сосредоточимся на этом сейчас.
Почему математика так важна в информатике?
Представьте себе Бурдж-Халифа , (самое высокое здание в мире). Итак, что является самой важной частью этого здания? Нет, дело не в высоте (ну, тоже!), А в основном в основании. Если бы у Бурдж-Халифа не было прочного основания, она была бы довольно шаткой и с большей вероятностью упала бы, чем устояла !!
Теперь, если вам интересно узнать об этой истории, не относящейся к теме, математика — это фундамент, на котором построены компьютерные науки (Бурдж-Халифа… понимаете ?!).Фактически, можно даже сказать, что информатика — это подмножество математических наук в целом. Как же так? Что ж, некоторые моменты, демонстрирующие это, приведены ниже:
1. Дискретная математика — основа информатики
Вы когда-нибудь слышали о логической нотации, теории множеств, комбинаторике, теории графов, вероятности, теории чисел, алгебре и т. Д.? Не удивляйтесь, все это часть дискретной математики, а также базовая основа программирования и информатики (а это значит, что вам нужно изучать их для информатики !!!).
Ярким примером этого является алгебра. В то время как логическая алгебра используется в логических воротах, реляционная алгебра используется в базах данных. Если вам нужен еще один пример, у теории чисел есть несколько приложений в криптографии и криптоанализе. (Видите, насколько это важно ?!)
2. Математика учит использованию алгоритмов
Алгоритмы являются фундаментальной частью компьютерных наук, и все вы, должно быть, слышали о них так или иначе (если нет … вам нужно учиться снова !!!). По сути, они представляют собой набор инструкций, демонстрирующих реализацию программы или приложения.
Итак, где вы впервые использовали алгоритм? Это был не класс информатики, а математика! Не верите? !! Итак, «2 + 3 = 5» — это базовый алгоритм, который вы изучили на уроке математики, который демонстрирует сумму 2 и 3. Математика на самом деле очень важна для изучения базового использования алгоритмов, которые используются в продвинутой форме в информатике.
3. Математика обеспечивает аналитические навыки, необходимые в компьютерных науках
Аналитические навыки необходимы для решения проблем и анализа данных.И угадайте, где вы впервые примените эти навыки? Математика!!! Да, математика всегда заставляет вас анализировать свои уравнения и понимать процесс вывода в случае ошибки. Эту ошибку необходимо исправить, чтобы получить окончательное решение.
Это дает множество аналитических навыков, которые можно использовать позже при поиске и исправлении ошибок !!! Несмотря на то, что существуют современные инструменты, которые могут выполнять эту работу автоматически, опыт и знания, полученные о выполнении программы и отладке, неоценимы.
4. Математические концепции необходимы во многих дисциплинах информатики
Информатика — это общий термин, который включает в себя множество дисциплин, таких как операционные системы, базы данных, сети, искусственный интеллект, встроенные системы, аналитика данных… !! И хотя есть некоторые дисциплины, с которыми вы можете справиться с минимальными знаниями математики, для большинства из них требуется хотя бы некоторый уровень компетенции.
Например, такие области, как искусственный интеллект и машинное обучение, требуют глубоких знаний математических понятий, таких как линейная алгебра, многомерное исчисление, теория вероятностей и т. Д.(И это делает математику очень важной !!!)
Итак, какой вывод?
Действительно ли математика необходима компьютерным наукам? Кто-то скажет, что это зависит от работы. Например: создание блога о еде не обязательно требует каких-либо знаний математики. Но создание успешного блога — это совсем другое дело. Это требует сосредоточения внимания на предпочтениях аудитории, популярности темы, рейтингах статей и т. Д. И угадайте, что… Для всего этого требуется математика.
Итак, да… Математика лежит в основе компьютерных наук.И если вы хотите преуспеть в какой-либо дисциплине компьютерных наук, гораздо лучше привить любовь к математике, поскольку это вам очень поможет.
Краткий обзор степеней, экспонент и научных обозначений
=== Боб Сазерленд ===
Краткий обзор базовой терминологии и символов, используемых для обозначения степеней, показателей, квадратных корней, кубических корней и научных обозначений.
Степени и экспоненты в математике
В неполной средней школе ваш учитель математики называл их степеней .В старших классах средней школы ваш учитель математики изменил свое имя на экспонентов . В классах математики средней школы степени и степень — это два разных слова, означающих одно и то же.
В 53 базовое число равно 5, а степень или экспонента равна 3. Показатель показывает, сколько раз нужно умножить базовое число само на себя.
В некоторых учебниках по математике и информатике число с основанием называется основанием .
51 = 5
52 = 5 х 5 = 25
53 = 5 х 5 х 5 = 125
54 = 5 х 5 х 5 х 5 = 625
Любое базовое число с нулевым показателем степени равно единице.
Следовательно, 1 = 20 = 30 = 40 = 50 = 60 и так далее.
Показатель степени 1/2 означает нахождение квадратного корня из числа.
Показатель степени 1/3 означает нахождение кубического корня числа.
Отрицательный показатель степени означает, что у вас есть дробь с единицей в числителе.
Экспоненты на компьютере
В первые годы существования компьютеров единственным общедоступным программным обеспечением были языки программирования. При использовании компьютерного языка программирования все символы нужно было вводить в виде простых букв и цифр в одной строке. Невозможно было ввести маленькую экспоненту рядом с верхним правым углом большего основного числа.
Чтобы попытаться решить эту проблему и другие проблемы, связанные с попыткой ввода математических символов и обозначений на компьютере, первые изобретатели языков компьютерного программирования придумали ряд альтернативных решений. перед экспонентой. Это обозначение все еще существует и используется людьми сегодня. Хотя не все знают и не признают, это то, что я бы порекомендовал вам использовать, когда вы не можете вводить маленькие надстрочные индексы для экспонент рядом с большим основным числом.
К счастью, изобретатели языков компьютерного программирования намного лучше достигли соглашения об использовании звездочки * в качестве знака умножения и косой черты / в качестве знака деления на компьютере.Символ ÷ , используемый для разделения в классах математики, не был доступен в качестве клавиши на клавиатуре компьютера. Использование клавиши с буквой x как для знака умножения, так и для буквы x может привести к путанице, особенно для студентов, изучающих математику средней школы, где буквы x и y часто используются в качестве переменных в уравнениях и формулах. (0.2) = 1 / (7 * 7) = 1/49
Подсказка: вам нужно будет довольно часто использовать скобки при вводе математических уравнений в одну строку, чтобы избежать двусмысленности в значении.
Научная нотация
Научная нотация — это альтернативный метод записи очень широких чисел, в которых много цифр до или после десятичной точки. Например, при измерении расстояний в космосе между планетами и звездами мы можем использовать научные обозначения.
Числа в научной системе обозначений записываются как число от единицы до десяти, умноженное на десять в степени.
Степень десяти легко найти, потому что это просто количество разрядов, на которое нужно переместить десятичную точку, чтобы поставить десятичную точку после первой цифры.
Вот несколько примеров преобразования числа в научное представление:
39485,72 = 3,948572 x 104
0,0000261 = 2,61 x 10-5
0,000000000082700394 = 8,2700394 x 10-11
Среднее расстояние от Нептуна до Солнца в Километрах:
Научная запись на компьютере
Когда число содержит слишком много цифр, чтобы компьютер мог сохранить число в своей памяти или отобразить число на своем экране, компьютер преобразует число в экспоненциальное представление.Числа, представленные в экспоненциальном представлении, следует рассматривать как округленные.
В экспоненциальном представлении на компьютере число будет вводиться в одну строку со всеми символами одинакового размера и без пробелов. После первой цифры будет десятичная точка. Буква e для экспоненты заменит x 10 , используемую в обычном научном представлении. Показатель степени будет состоять из знака плюс или минус, за которым следует число.
| Научная нотация | Научная нотация на компьютере |
|---|---|
| 5.683 x 108 | 5.683e + 8 |
| 1.928445 x 10-15 | 1.928445e-15 |
| 9,9937 x 10-34 | 9.9937e-34 |
| 1.0003 | +24
4 Абстракция, представление и обозначения | Информатика: размышления о поле, размышления о поле
ЯЗЫКИ ПРОГРАММИРОВАНИЯ И КОМПЬЮТЕРНЫЕ НАУКИАльфред В.Ахо, Колумбийский университет, и Джеймс Ларус, Microsoft Research
Программное обеспечение влияет на жизнь практически каждого современного человека, часто глубоко, но мало кто ценит огромный размер и размах мировой инфраструктуры, стоящей за ним, или текущие исследования, направленные на ее улучшение. В настоящее время используются сотни миллиардов строк программного кода, и многие миллиарды добавляются ежегодно, и они фактически запускают весь спектр мыслимых приложений. Все это программное обеспечение стало возможным, потому что нам удалось изобрести широкий спектр языков программирования для описания задач, которые мы хотим, чтобы компьютеры выполняли.Но, как и человеческие языки, они иногда бывают причудливыми и несовершенными. Таким образом, компьютерные ученые постоянно разрабатывают более точные, выразительные и удобные способы, которыми люди могут общаться с компьютерами.
Языки программирования во многих отношениях отличаются от человеческих языков. Компьютер способен выполнять арифметические или логические операции с невероятной скоростью, но на самом деле это устройство поразительно простое — навсегда закрепленное в конкретном мире битов, байтов, арифметики и логики (см. Хилл в главе 2).Таким образом, компьютеру должны быть даны простые, однозначные, пошаговые инструкции. Люди, напротив, часто могут решать очень сложные проблемы, используя свои врожденные способности формулировать и применять абстракции.
Чтобы почувствовать масштабы этого «семантического разрыва», представьте, что вы объясняете маленькому ребенку, как приготовить еду. Учитывая, что у ребенка, скорее всего, нет опыта или контекста, на который можно было бы опираться, каждый шаг должен быть описан четко и полностью, а пропуск даже самых простых деталей может привести к неприятной неудаче.Объяснение задач компьютерам во многих отношениях сложнее, потому что компьютеры не только требуют гораздо большего количества деталей, но эти детали также должны быть выражены в примитивных, трудных для чтения обозначениях, таких как двоичные числа.
В качестве примера того, как языки программирования устраняют разрыв между программистами и компьютерами, рассмотрим числовые вычисления, одно из самых ранних приложений компьютеров, относящееся ко времени Второй мировой войны. Обычная математическая операция — это умножение двух векторов чисел.Люди будут использовать обозначение, такое как A * B, для обозначения умножения (то есть скалярного произведения) вектора A и вектора B, зная, что это сокращение для всех отдельных шагов, фактически необходимых для выполнения умножения. С другой стороны, компьютеры ничего не знают о векторах или правилах их умножения. Они могут только перемещать числа; выполнять сложение, умножение и другие примитивные математические операции —
N-обозначение | Хайбров
Эпизод # 2 курса Курта Андерсона по основам информатики
С возвращением!
Вчера мы рассмотрели основы работы самих компьютеров.Сегодня мы изучим строительные блоки анализа алгоритмов — ключевой концепции информатики.
Что такое N-нотация?
N-нотация — это способ представления времени выполнения алгоритма, чтобы его можно было сравнить с другим алгоритмом. N-нотация — это НЕ анализ того, сколько времени потребуется для выполнения алгоритма, а анализ того, как алгоритм будет масштабироваться с увеличением количества входных данных.
Этот метод основан на просмотре входных данных алгоритма и анализе того, как алгоритм работает с этими входными данными.Однако мы точно не знаем, сколько данных будет поступать в любой момент. Что мы делаем, так это заменяем этот входной номер переменной n .
Например, предположим, что у нас есть алгоритм, который проверяет количество ваших друзей в Facebook. Когда мы пишем алгоритм, мы понятия не имеем, сколько друзей будет добавлено в качестве входных данных. У вас может быть 25, 2000 или два. Таким образом, вместо того, чтобы указывать фактическое число, мы просто говорим, что n частей данных будут помещены в этот алгоритм.
Как использовать N-нотацию
Как использовать это для сравнения двух алгоритмов? Что мы делаем, так это ищем существенные различия в алгоритмах. Как программа реагирует на ввод n ?
© Cmglee
На приведенной выше диаграмме мы можем увидеть эти различные отношения в графическом виде. Ось x (нижняя часть графика) показывает, сколько частей данных поступает в алгоритм.Ось Y (левая сторона) показывает, сколько операций придется выполнить программе с учетом количества фрагментов данных.
Что же тогда показывает эта диаграмма? Это показывает отношения, о которых мы говорили. Центральная зеленая линия — n . Это означает, что если мы вставим n частей данных, алгоритм займет n операций. На сотню фрагментов данных потребуется 100 операций, на 200 — 200 и так далее. Обратите внимание, что для некоторых других строк требуется существенно больше операций при том же количестве ввода.
Реальным примером этого может быть копирование рукописной электронной таблицы в Excel. В данном случае вы являетесь алгоритмом. Для каждой части данных на этой бумажной копии вам нужно будет выполнить одну операцию, вставив ее в Excel. Если имеется 100 единиц данных, потребуется 100 операций вставки. Каким бы ни был размер ввода, вам придется проделать столько операций. Это делает время выполнения для этого n .
Допустим, вместо этого нам поручено проверить электронную таблицу и посмотреть, совпадает ли какое-либо значение с любым другим значением.2 (т.е. n * n).
Ключевым моментом здесь является осознание сложности проблем по мере их масштабирования. Первая проблема довольно проста. У вас может быть 1000 или 100000 страниц, и проблема не выйдет из-под контроля. Это могло надоесть, но за несколько часов ничего нельзя было решить.
При сравнении, однако, представьте, что проверяете полные 1000 страниц для каждого отдельного числа. Что делать, если у вас 10 000 или 100 000 страниц? Проблема быстро становится неуправляемой. Это то, на что мы смотрим с помощью n-нотации — это взаимосвязь между исходными данными и ростом проблемы.
Вот сравнение того, как разные алгоритмы могут работать с реальными числами.
Ключевые выносы:
• N-нотация используется для сравнения роста алгоритмов, а не их фактического времени.
• N используется как переменная для количества блоков данных, вводимых алгоритмом. Затем мы смотрим на взаимосвязь с тем, сколько операций он должен выполнить при таком количестве входных данных.
Завтра мы расширим эту идею с помощью нотации Big O.
Ура,
Курт
Рекомендуемая книга
Элементы вычислительных систем: построение современного компьютера из первых принципов Ноам Нисан, Шимон Шокен
Поделиться с друзьями
.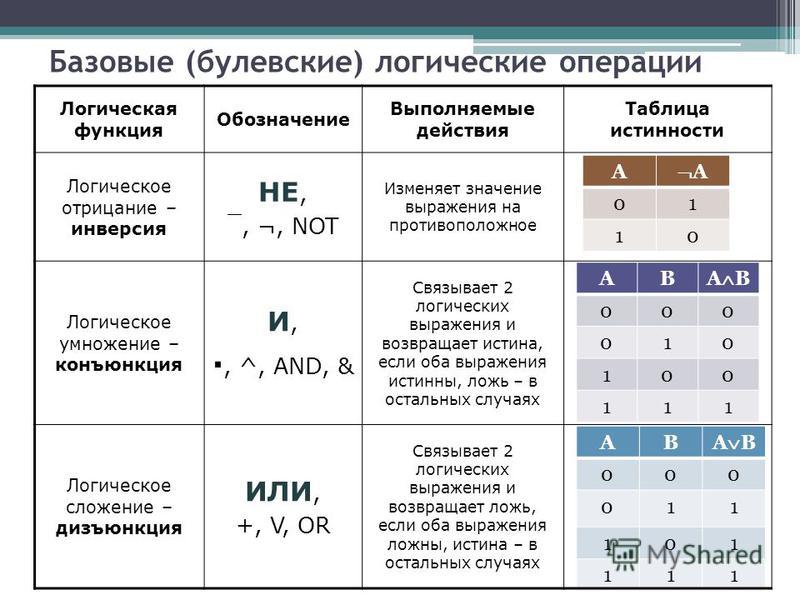 Составное высказывание А ИЛИ В будет истинным, если истинно хотя бы одно из двух составляющих его простых высказываний. Для записи логической операции ИЛИ можно использовать следующие выражения: A ИЛИ B, A OR B, A + B, A∨ B, A | B.
Составное высказывание А ИЛИ В будет истинным, если истинно хотя бы одно из двух составляющих его простых высказываний. Для записи логической операции ИЛИ можно использовать следующие выражения: A ИЛИ B, A OR B, A + B, A∨ B, A | B.