Знаки больше и меньше в математике — сравнение чисел с примерами
Знаки больше и меньше в математике становятся известны детям еще до поступления в первый класс. Часто детки путают, что означает конкретный символ. Родители могут помочь своим чадам в этом вопросе, что положительно повлияет на успеваемость детей. Эти знания пригодятся малышам и в будущем – при изучении геометрии, на уроках алгебры, в примерах, где используется квадратная, а также другая степень чисел. Советы из дан статьи помогут родителям научить малышей важной математической премудрости.
Математические знаки в картинках для дошкольников
Ниже представлено цветное оформление математических символов. При обучении их можно использовать непосредственно с экрана монитора или же их можно распечатать на цветном принтере.
Знак «больше» – в какую сторону
Знак «больше» пишется так «>».
Знак «меньше» – как правильно писать
Знак «меньше» выглядит так «<». Если сказать просто, то стрелка должна смотреть влево. И снова для определения важна левая часть стрелки. Если точка, из которой выходят две линии, расположена слева, то это символ «<».
Знаки «больше или равно» / «меньше или равно»
Знаки «больше или равно» и «меньше или равно» выглядят соответственно так «≥», «≤». Они являются результатом объединения двух символов – «>» или «<» и одной линии.
Эта линия находится под стрелкой. При этом нет пересечения стрелки с линией под ней. Обычно нижняя линия следует принципу параллельности по отношению к нижней части символа.
Данные знаки используются в нестрогих неравенствах. В первом классе такие неравенства обычно не изучают.
Примеры на сравнение чисел для 1 класса
В первом блоке примеров (Таблица 1) нужно поставить правильный символ. Справа и слева стоят только однозначные числа.
Второй блок примеров (Таблица 2) содержит примеры, в которых нужно сопоставить суммы чисел. В случае равенства необходимо вписать знак «равно».
Игры для быстрого запоминания знаков «больше» и «меньше»
Существуют различные логические игры с использованием математических символов. Таких игр множество. Ниже приводятся три игры, где детям нужно поиграться со стрелками «>» и «<».
Игра «Большой голодный крокодил»
Это самый легкий и наглядный способ раз и навсегда запомнить, в какую сторону пишутся знаки «больше» и «меньше».
На каждую из «тарелок» можно положить что-то приблизительно напоминающее еду. Например, можно слепить шарики из пластилина или соленого теста и договориться с ребенком, что горошины означают котлеты для крокодила. Для этой игры достаточно смастерить один символ. Его можно сделать на маленькой карточке. Обозначения «>» и «<» примерно напоминают подобие раскрытого рта крокодила.
Важное условие — крокодил выбирает всегда только ту тарелку, на которой больше еды! Об этом нужно сказать ребенку.
На обе «тарелки» необходимо выложить определенное количество «котлет». Затем пусть ребенок положит карточку так, чтобы «рот крокодила» был обращен в сторону «тарелки» на которой больше «котлет».
Игра «Что больше?»
В этой игре комбинация большого и указательного пальцев левой руки имеет значение символа «<», а комбинация большого и указательного пальцев правой руки представляет собой символ «>». Для обозначения того, что больше, достаточно протянуть правую руку, а левая рука нужна для обозначения того, что меньше.
Для обозначения того, что больше, достаточно протянуть правую руку, а левая рука нужна для обозначения того, что меньше.
В этой игре для сравнения можно использовать не только числа, но и изображения различных предметов, а также геометрические фигуры разных размеров. Эту игру-занятие можно выполнять во время приема пищи, разложив на столе печенье, конфеты, яблоки и другие продукты. Вот так можно запомнить правильное написание знаков задолго до школы.
Игра «Кубики и доски»
Эта игра принадлежит к разряду активных игр, так как детям нужно совершать действия не только умственного характера, но и быть активными строителями. Для этой игры понадобятся следующие принадлежности: большие кубики и две прямых доски. Одну доску нужно положить на горизонтальную поверхность. На оба края лежащей доски нужно выложить кубики в столбики.
Важно чтобы столбики быть ровными, как восклицательный знак. К примеру, первый (левый) столбик состоит из 4-х кубиков, а второй из 2-х.![]() Затем нужно положить вторую доску на оба столбика. В итоге сочетание нижней и верхней досок покажет правильный символ. В данном примере получится обозначение «>».
Затем нужно положить вторую доску на оба столбика. В итоге сочетание нижней и верхней досок покажет правильный символ. В данном примере получится обозначение «>».
С каждым последующим разом можно изменять количество кубиков в столбиках. Когда столбики будут содержать одинаковое количество кубиков – доски покажут «равно».
Заключение
Итак, в математике обозначения «>» и «<» используются довольно часто. Малыши способны освоить принцип их применения довольно рано. Воспользовавшись советами из этой статьи, родители помогут своим детям сделать это быстро и в увлекательной форме.
Конспект урока по теме: Знаки больше, меньше и ровно.
 | План-конспект урока по математике (1 класс) по теме:
| План-конспект урока по математике (1 класс) по теме:Тема: Знаки: больше, меньше и равно.
Ход урока
1. Организационное начало урока
Чтобы хорошо учиться,
Надо очень много знать.
Каждый день копилку знаний
Непременно пополнять.
2. Актуализация знаний
— Сегодня мы познакомимся со знаками «больше», «меньше» и «равно». Научимся сравнивать предметы. А в этом нам поможет сказочный герой. Угадайте какой.
Такой же озорник, как буква «Б»,
Пассажир немного странный,
Человечек деревянный,
На земле и под водой
Ищет ключик золотой.
Всюду нос суёт он длинный.
Кто же это?… Буратино!
1) Устный счёт
— Посчитайте от 10 до 30 и наоборот.
— Какие числа стоят после чисел три, четыре, два? Четыре, пять, три.
— Какие числа стоят перед числами один, пять, два? Ноль, четыре, один.
— Соседями какого числа являются числа 4 и 6? Пять.
— Два и четыре? Три.
— Ноль и два? Один.
— Три и пять? Четыре.
— Решите примеры.
— Один прибавить два равно –… три.
— Два прибавить два равно –… четыре.
— Три прибавить два –…пять.
— Четыре прибавить один – …пять.
— Из пяти вычесть два будет – …три.
— Четыре вычесть три равно –…один.
— Три вычесть один равно –…два.
— Пять вычесть три равно –…два.
— Четыре минус два будет –…два.
— Помогите Буратино справиться с примерами.
4-1=3
5-2=3
3+1=4
3+2=5
2+2=4
— Рассмотрите внимательно картинки и подберите к ним примеры.
Я рисую кошкин дом:
Три окошка, дверь с крыльцом.
Наверху ещё окошко,
Чтобы не было темно.
Посчитай окошки
В домике у кошки.
— Четыре, так как к трём прибавить один получится – четыре.
Сидит у окошка серая кошка,
Лежит на рогожке рыжая кошка.
Играет с мышонком чёрная кошка,
Залезла в лукошко белая кошка.
Сколько же кошек?
Не сбейся, смотри.
Сколько ты насчитал?
Говори!
— Четыре, потому что один плюс один, плюс один, плюс один получится – четыре.
— На горке катались две девочки и три мальчика. Сколько детей каталось на горке?
— Два да ещё три будет – пять.
— Двое мальчиков ушло. Сколько детей осталось на горке?
-Пять без двух будет – три.
— Сколько квадратов нарисовано?
— Конечно же, пять.
Физкультминутка для пальчиков
Вот все пальчики мои,
Их как хочешь поверни.
И вот этак, и вот так,
Не обидятся никак.
Раз, два, три, четыре, пять –
Не сидится им опять.
Постучали,
Повертели
И работать захотели.
Дали ручкам отдохнуть,
А теперь обратно в путь.
Актуализация знаний 2
2. Формирование знаний
— Сколько грибов слева? Три.
— Сколько грибов справа? Два.
— Где грибов больше? Конечно же, слева.
— Мы можем это обозначить при помощи знака «больше». Этот знак открывает свой «клювик» в сторону большего числа.
— Читаем так: «Три больше двух». Запишите это, проговорив ещё раз.
Как нам быть, когда число
Больше будто бы назло?
Как же это показать,
Чтобы каждый смог понять?
Вот для этого, друзья,
«Больше» знак рисую я.
Он от большего числа
Отлетает, как стрела,
И указывает нам
На того, кто меньше.
— Сколько яблок слева? Четыре.
— Сколько яблок справа? Пять.
— Где меньше яблок? Слева.
— Мы можем это записать при помощи знака «меньше». Этот знак обращён уголком в сторону меньшего числа, то есть закрытым «клювиком» указывает на меньшее число. Читаем так: «Четыре меньше пяти». Запишите это, проговорив ещё раз.
С большой цифрой повезло.
Где же меньшее число?
А его, каждый знает,
«Меньше» знак обозначает.
Это тот же самый знак,
Но стоит совсем не так:
Словно сделав кувырок,
Катит цифру в левый бок.
Это значит, что она
Только меньшей быть должна.
— Как сделать так, чтобы грибов было одинаковое количество?
— Правильно, нужно добавить или убрать один гриб.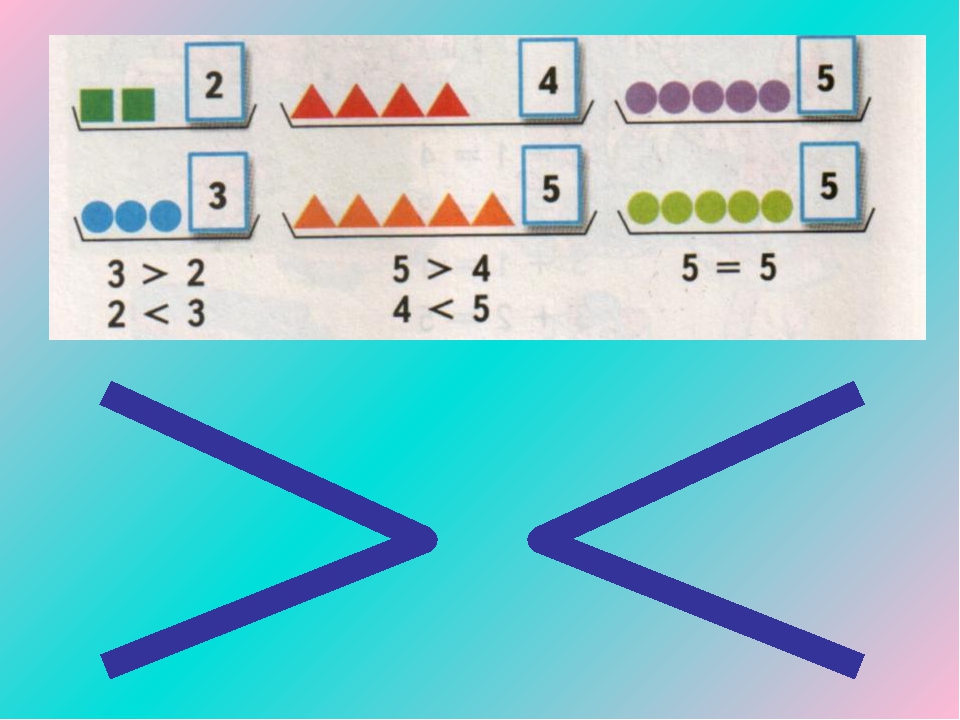
— Это можно записать при помощи знака «равно». Читаем так: «Три равно трём»
— Как уровнять яблоки?
— Прочитайте надпись и запишите её.
Если просто мы сравним
Два числа, одно с другим,
И увидим, что они
По значению равны, —
Ставим, так заведено,
Между ними знак «равно».
Этот знак, запомни ты,
Выглядит как две черты.
У него такая слава:
Слева столько, сколько справа.
— Сколько шаров слева? Два.
— Сколько шаров справа? Один.
— С какой стороны больше шаров? Слева больше шаров.
— Почему справа цифра «один»? Правильно, потому что справа один шар.
— Правильно ли поставлен знак «больше»? Докажите.
— Конечно же, правильно. Ведь два больше, чем один, поэтому «клювик» открыт в сторону большего числа.
Физкультминутка
Сколько раз ударю в бубен,
Столько раз дрова нарубим.
Приседаем столько раз,
Сколько мячиков у нас.
Сколько покажу кружочков,
Столько сделаем прыжочков.
Актуализация знания 3
3.Закрепление знаний
— Чего меньше: легковых машин или грузовых машин? Верно, грузовых машин.
— Как это записать? Три меньше четырёх.
— Чего больше: легковых машин или автобусов? Правильно, легковых машин.
— А это как записать? Четыре больше одного.
— Если приехало ещё два автобуса, то чего больше автобусов или легковых машин?
— Верно, легковых машин больше. Это можно записать так: один плюс два меньше четырёх.
— Все эти записи называют неравенствами.
— Чего теперь больше: автобусов или грузовых машин? Их одинаковое количество.
— Эти записи называются равенствами.
4-1=3 3+11
5-1>2 4+1=5 1+2=3
— Выписать в один столбик равенства, а в другой – неравенства.
— Проверь себя!
4-1=3 5-1>2
4+1=5 3+1
1+2=3 1+2>1
— Расселите числа по этажам.
— Проверь себя!
— Сколько палочек нужно взять, чтобы построить треугольник? Три.
— Возьмите четыре счётные палочки и постройте новую фигуру.
— Как эта фигура называется?
— Она называется четырёхугольник, потому что у неё четыре стороны и четыре вершины. Если у четырёхугольника прямые углы, то он называется прямоугольником.
— Если я возьму шесть палочек и выложу такую фигуру, то как она будет называться? Почему?
— Правильно – это шестиугольник, потому что у него шесть сторон и шесть вершин.
▲▲ ■■■■ ○○○○○
▲ ■■□□ ○○○○
2>1 4* 2+2 5* 4-1
□□□
□□□□
3*4
— Сравни предметы, запиши неравенства и вставь нужные знаки.
— Проверь себя!
— Юра и Оля измеряли расстояние от дома до дерева при помощи шагов. Почему у них получились разные ответы?
— Правильно, у них разная длина шага.
1+3 5-4
2+1 4-2
4+1 3-2
1+1 5-1
— Повесь вёдра на коромысла, предварительно решив пример.
— Проверь себя!
— Один ослик нёс 10 килограммов сахара, а другой – 10 килограммов ваты. У кого поклажа была тяжелей?
— Поклажа была одинаковой. Несмотря на то, что размеры разные, но вес одинаковый.
3. Подведение итогов
— В какой руке знак «
— В какой руке знак «>»? В правой.
— Что обозначает знак «=»? Равенство.
3+2=5 4>3
4=4 1
— Назовите равенства.
— Три плюс два, равно пять. Четыре равно четырём.
— Назовите фигуры.
Рефлексия
Сегодня на уроке:
Я узнал…
Я научился …
Мне было интересно…
Мне было трудно…
Буратино прощается с вами. До новых встреч!
1 класс — Сравнение предметов, больше, меньше, равно
Дата публикации: .
Урок и презентация на тему: «Математические знаки: больше, меньше, равно»
Есть прекрасная страна «Математика». В ней живут не только числа, но и математические знаки, которые желают с вами познакомимся. А поможет нам в этом маленький Лисёнок. Он учится в Лесной школе, поэтому он вместе с вами познакомиться с математическими знаками.
А поможет нам в этом маленький Лисёнок. Он учится в Лесной школе, поэтому он вместе с вами познакомиться с математическими знаками.
На уроке Лисёнку дали задание – посчитать сколько котят и щенят нарисовано на картинке. Давайте поможем ему в этом.
Сколько котят и сколько щенят изображено на рисунке? Кого больше, а кого меньше?
А теперь давайте изобразим количество котят и щенят цифрами.
В математике неравенства обозначаются знаками «больше» и «меньше». Чтобы вам было легче запомнить, какой из них какой, давайте представим себе уточку, которая крякает. Её открытый клювик всегда будет показывать на уменьшение.
Посмотрите внимательно на уток: куда они сморят. Как ты думаешь, где знак «больше», а где «меньше»?
Так в математике выглядят знаки «больше» и «меньше».
Так какой мы должны поставить здесь знак? Правильно, знак «больше».
Реши задачу. Ёжик получил в подарок от Белки грибочки, а Зайчик морковки. Посчитай сколько грибочков получил Ёжик, а сколько морковки получил Зайчик? Посчитай, чего больше грибочков или морковок?
Помоги Лисёнку посчитать и сравнить сколько на картинке клубники, а сколько бананов? Расскажи: чего больше, чего меньше?
Лисёнок пошёл в лес собирать грибы и на полянке увидел лисички и мухоморы. Каких грибов больше? Поставь нужный знак.
Каких грибов больше? Поставь нужный знак.
В математике есть ещё один важный знак. Посмотри на картинку. Посчитай, сколько стручков гороха справа и слева?
Стручков поровну – по 12 штук. Между нами нужно поставить знак «равно». Вот так он выглядит.
Знак «равно».
Теперь Вы знаете, что в математике есть три важных знака:
Сегодня вы с Лисёнком узнали самые важные математические знаки. Вспомните их.
Сравнение натуральных чисел, знаки сравнения. Онлайн калькулятор
Равные и неравные натуральные числа
Если записи двух натуральных чисел одинаковы, то говорят, что эти числа равны между собой. Числа, которые равны, называются равными. Если записи двух натуральных чисел отличаются, то говорят, что эти числа не равны. Числа, которые не равны, называются неравными.
Числа, которые не равны, называются неравными.
Пример. Натуральное число 34 равно числу 34 (их записи одинаковы), а натуральные числа 63 и 67 не равны (их записи различны). Следовательно числа 34 и 34 — равные, а 63 и 67 — неравные.
Равенства и неравенства
Для записи результата сравнения чисел используются следующие знаки:
=, > и <.
При записи сравнения эти знаки располагают между числами.
Первый знак =
называется знаком равенства и заменяет собой слово равно
или равняется
. Например, если числа a и b равны, то пишут a = b и говорят: a равно b
.
Запись, которая состоит из математических выражений, между которыми ставится знак =
называется равенством.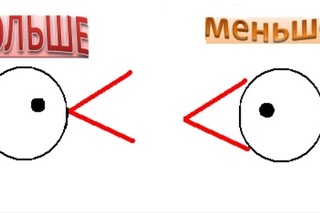
Пример.
4 = 4 — равенство.
2 + 3 = 5 — равенство.
2 + 2 = 1 + 1 + 2 — равенство (подобные записи представляют собой равенство двух числовых выражений, и означают равенство значений этих выражений).
Равенства могут быть как верными (например, 5 = 5 — верное равенство), так и неверными (например, 11 = 14 — неверное равенство).
Два других знака >
и <
называются знаками неравенства и означают: знак >
— больше
, а знак <
— меньше
. Например, если число a больше числа b, то пишут a > b и говорят: a больше b
или пишут b < a и говорят: b меньше a
.
Знаки >
и <
должны быть обращены остриём к меньшему числу.
Запись, которая состоит из математических выражений, между которыми ставится знак >
или <
называется неравенством.
Пример.
5 > 4 — неравенство.
2 < 7 — неравенство.
2 + 3 < 7 — неравенство (подобные записи представляют собой неравенство двух числовых выражений, и означают неравенство значений этих выражений).
Неравенства могут быть как верными (например, 2 < 9 — верное неравенство), так и неверными (например, 5 > 8 — неверное неравенство).
Кроме неравенств со знаками >
и <
, которые называются строгими, используются нестрогие неравенства, для которых введены знаки ⩾
и ⩽
. Знак ⩾
читается больше или равно
, знак ⩽
— меньше или равно
. Нестрогое неравенство допускает случай равенства левой и правой его частей. Так, например, 7 ⩽ 7 — верное неравенство.
Также для записи неравенства двух натуральных чисел может применяться знак ≠
. Знак
Знак ≠
читается не равно
. Например, запись a ≠ b — означает a не равно b.
Обычно, если не оговорено иное, понятие неравенства относится только к записям со знаками >
, <
, ⩾
и ⩽
.
Правила чтения равенств и неравенств
Равенства и неравенства читаются слева направо. Левая часть равенства читается в именительном падеже, а правая — в дательном.
Пример. 7 = 7 — семь равно семи.
Левая часть неравенства читается в именительном падеже, а правая — в родительном.
Пример. 11 > 9 — одиннадцать больше девяти, 3 < 5 — три меньше пяти.
Правила сравнения чисел
Числа можно сравнивать двумя способами: с помощью натурального ряда и по их десятичной записи.
Правило сравнения с помощью натурального ряда:
Из двух натуральных чисел меньше то, которое в натуральном ряду встречается раньше (т. е. находится левее), и больше то, которое в натуральном ряду встречается позже (т. е. находится правее).
е. находится левее), и больше то, которое в натуральном ряду встречается позже (т. е. находится правее).
Следовательно, в натуральном ряде каждое число, кроме 1, больше предыдущего.
Пример. Сравним числа 1 и 3, 7 и 4. Запишем все однозначные натуральные числа в одной строке в следующем порядке:
1, 2, 3, 4, 5, 6, 7, 8, 9.
Число 1 меньше числа 3 (1 < 3), так как в натуральном ряду число 1 находится левее числа 3. Число 7 больше числа 4 (7 > 4), так как в натуральном ряду число 7 находится правее числа 4.
Для применения правил сравнения чисел по их десятичной записи необходимо принять одну условность: будем считать, что число 0 меньше любого натурального числа, и что нуль равен нулю.
Правила сравнения натуральных чисел по их десятичной записи:
Если записи сравниваемых чисел состоят из одинакового количества цифр, то числа сравниваются поразрядно слева направо. Большим будет считаться то число, у которого первая (слева направо) из неодинаковых цифр больше.
Большим будет считаться то число, у которого первая (слева направо) из неодинаковых цифр больше.
Когда говорят, что цифры равны (или одна цифра больше другой), то имеют ввиду, что соответствующие им числа равны (или одно число больше другого).
Пример. Сравним натуральные числа 4026 и 4019. Для удобства сравнения можно записать их одно под другим:
4026
4019
Сначала сравниваем значения разряда тысяч. Получаем равенство 4 = 4, поэтому переходим к сравнению значений следующего разряда. Опять получаем равенство 0 = 0, переходим к сравнению значений разряда десятков. Теперь имеем неравенство 2 > 1, из которого делаем вывод, что число 4026 больше числа 4019 (4026 > 4019), потому что у первого числа, цифра разряда десятков (2) больше, чем цифра разряда десятков (1) у второго числа.
Если количество цифр в записи, сравниваемых чисел, разное, то большим будет считаться то число, у которого количество цифр больше.
Пример. Сравним натуральные числа 347 503 и 34 503. Для удобства сравнения можно записать их одно под другим:
Записав числа одно под другим, можно наглядно заметить, что первое число имеет большее количество цифр, чем второе, следовательно 347 503 > 34 503.
Два натуральных числа равны, если у них одинаковое количество цифр и цифры одинаковых разрядов равны.
Пример. Сравним числа 38 526 734 и 38 526 734. Для удобства сравнения можно записать их одно под другим:
38 526 734
38 526 734
Записи данных чисел одинаковы (количество цифр и цифры одинаковых разрядов равны), следовательно эти числа равны.
Двойные неравенства, тройные неравенства и т. д.
Когда нужно записать, что одно число больше другого, но меньше третьего, часто используют двойные неравенства.
Пример. Известно, что 4 < 7, а 7 < 16. Эти два неравенства удобнее представить в виде двойного неравенства:
Известно, что 4 < 7, а 7 < 16. Эти два неравенства удобнее представить в виде двойного неравенства:
4 < 7 < 16.
Двойные неравенства принято читать с середины. Например, неравенство 2 < 4 < 5 читается так: четыре больше двух, но меньше пяти
.
В виде двойного неравенства можно записывать результат сравнения трёх натуральных чисел.
Пример. Допустим, нужно сравнить три натуральных числа 11, 34 и 8. Сравнивая данные числа между собой, получим три неравенства 11 < 34, 8 < 11 и 34 > 8, которые можно записать как двойное неравенство:
8 < 11 < 34.
Аналогичным образом строятся тройные, четверные и т. д. неравенства.
Пример. Известно, что 12 < 15, 47 > 15, 47 < 112, тогда можно записать
12 < 15 < 47 < 112.
Калькулятор сравнения чисел
Данный калькулятор поможет вам сравнить натуральные числа. Просто введите два числа и нажмите кнопку
Просто введите два числа и нажмите кнопку Сравнить
.
Математические знаки и символы на английском
Основные математические знаки и символы на английском языке (плюс, минус, деление, умножение и другие, менее распространённые знаки и символы).
* — для самостоятельно изучающих английский язык также могут быть интересными разделы «Фильмы на английском» и «Аудиокниги на английском».
В данной статье мы рассмотрим наиболее распространенные математические знаки и символы на английском языке. Графическое изображение математических знаков и символов универсально во всех языках, но их звучание и произношение значительно отличаются друг от друга. Если вы работаете за границей или даже просто общаетесь на английском с друзьями, вам необходимо знать произношение основных символов на английском языке.
Математические знаки, использующиеся для основных арифметических действий:
«+» — plus — плюс
«-» — subtraction sign – знак вычисления
«x» — multiplication sign – знак умножения
«/» slash . .. divided by – косая линия. Этот математический символ в английском языке также употребляется в качестве знака деления.
.. divided by – косая линия. Этот математический символ в английском языке также употребляется в качестве знака деления.
«÷» division sign — знак деления
«:» — сolon – двоеточие; или ratio sign — знак отношения или деления в английском языке
«=» еqual sign – знак равенства
Эти математические знаки известны всем и употребляются повсеместно, поэтому нужно знать, как они звучат на английском языке.
Следующие математические символы не так распространены, но всё же не помешает их знание на английском:
«%» Percent symbol – математический символ в английском языке, который употребляется для обозначения процентов
«[ ]» square brackets – квадратные скобки
«±» рlus/minus sign — знак плюс/минус
«≈» аpproximate equal sign — приближенное равенство
«<» inequality sign (less than – меньше чем) — знак неравенства
«>» inequality sign (greater than – больше чем) — знак неравенства
« ≤ » inequality sign (less than or equal to . .. — меньше чем или соответствует …)
.. — меньше чем или соответствует …)
«{ }» сurly brackets (the quantity …… the set …- общее количество) — фигурные скобки
«√» surd (… root of … – корень из) — иррациональное число
«√» square root – квадратный корень
Математические знаки и символы очень разнообразны и отличаются сферой употребления. Ниже перечисленные математические знаки и символы менее распространены и употребляются в основном в специализированных областях. Вот написание ещё нескольких математических символов на английском:
«∫» — integral — интегральный
«i» — imaginary unit — мнимая единица
«z*» — complex conjugate — комплексно сопряжённая величина
«∇» — nabla/del — набла
«δ» — delta function — дельта-функция
«∞» — infinity symbol – символ бесконечности
«∅» null symbol — нуль или недействительный; несущественный
Вот еще несколько математических символов, которые используют в геометрии, которые на английском выглядят следующим образом:
«|» — perpendicular – перпендикулярный
«||» — parallel – параллельный
«≅» — congruent to – соответствующий (эквивалентность геометрических форм и размеров)
«∠» angle symbol – знак, который используют в геометрии для обозначения угла
Это лишь небольшой список наиболее употребляемых математических знаков и символов на английском, но, если углубиться в специализированную тематику, можно увидеть еще много знаков и символов, характеризующих различные понятия в данной сфере.
Что означает два знака больше – 4apple – взгляд на Apple глазами Гика
| Состояние | отпатрулирована |
В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeX, объяснения и примеры использования. Список и смысл обозначений соответствует международным стандартам ISO 31-11 и ISO 80000-2.
Кроме указанных символов, иногда используются их зеркальные отражения, например, A ⊂ B <displaystyle Asubset B>
обозначает то же, что и B ⊃ A .Знаки операций, или математические символы — знаки, которые символизируют определённые математические действия со своими аргументами.
Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как знак больше и знак меньше, а также знак равно.Однако, если с последним что-то напутать достаточно сложно, то о том, как и в какую сторону пишутся знаки больше и меньше (знак менее и знак более, как ещё их иногда называют) многие сразу после этой же школьной скамьи и забывают, т.к. они довольно редко используются нами в повседневной жизни.
Но практически каждому рано или поздно всё равно приходится столкнуться с ними, и «вспомнить» в какую сторону пишется нужный им символ получается лишь обратившись за помощью к любимой поисковой системе. Так почему бы не ответить развернуто на этот вопрос, заодно подсказав посетителям нашего сайта как запомнить правильное написание этих знаков на будущее?
Именно о том, как правильно пишется знак больше и знак меньше мы и хотим напомнить вам в этой небольшой заметке. Также будет не лишним рассказать и том, как набрать на клавиатуре знаки больше или равно и меньше или равно, т.к. этот вопрос тоже довольно часто вызывает затруднения у пользователей, сталкивающихся с такой задачей очень редко.
Содержание:
Перейдем сразу к делу. Если вам не очень интересно запоминать всё это на будущее и проще в следующий раз снова «погуглить», а сейчас просто нужен ответ на вопрос «в какую сторону писать знак», тогда для вас мы приготовили краткий ответ – знаки больше и меньше пишутся так, как показано на изображении ниже.
А теперь расскажем немного подробнее о том, как это понять и запомнить на будущее.
Как и в какую сторону пишется знак больше
В общем и целом логика понимания очень проста – какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону – такой и знак. Соответственно, знак больше влево смотрит широкой стороной – большей.
Пример использования знака больше:
- 50>10 – число 50 больше числа 10;
- посещаемость студента в этом семестре составила >90% занятий.
Как и в какую сторону пишется знак меньше
Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной – меньшей, то перед вами знак меньше.Пример использования знака меньше:
- 100 =», что, в принципе, часто вполне допустимо, но можно сделать красивее и правильнее.
На самом деле для того, чтобы напечатать эти знаки, существуют специальные символы, которые можно ввести на любой клавиатуре. Согласитесь, знаки «≤» и «≥» выглядят значительно лучше.
Знак больше или равно на клавиатуре
Для того, чтобы написать «больше или равно» на клавиатуре одним знаком даже не нужно лезть в таблицу специальных символов – просто поставьте знак больше с зажатой клавишей «alt». Таким образом сочетание клавиш (вводится в английской раскладке) будет следующим.
Или же вы можете просто скопировать значок из этой статьи, если вам нужно воспользоваться им один раз. Вот он, пожалуйста.
Знак меньше или равно на клавиатуре
Как вы наверное уже смогли догадаться сами, написать «меньше или равно» на клавиатуре вы можете по аналогии со знаком больше – просто поставьте знак меньше с зажатой клавишей «alt». Сочетание клавиш, которое нужно вводить в английской раскладке, будет следующим.
Или просто скопируйте его с этой страницы, если вам так будет проще, вот он.
Как видите, правило написания знаков больше и меньше довольно просто запомнить, а для того чтобы набрать значки больше или равно и меньше или равно на клавиатуре достаточно просто нажать дополнительную клавишу – всё просто.
Таблица обозначений абстрактной алгебры — В абстрактной алгебре повсеместно используются символы для упрощения и сокращения текста, а также стандартные обозначения для некоторых групп. Ниже приведён список наиболее часто встречающихся алгебраических обозначений, соответствующие команды в … Википедия
История математических обозначений — Математические обозначения это символы, используемые для компактной записи математических уравнений и формул[1]. Помимо цифр и букв различных алфавитов (латинского, в том числе в готическом начертании, греческого и еврейского),… … Википедия
Список математических аббревиатур — Статья содержит список общеупотребительных аббревиатур математических функций, операторов и др. математических терминов. Содержание 1 Аббревиатуры 1.1 Латиница 1.2 Греческий алфавит … Википедия
Набор символов Юникод — Юникод, или Уникод (англ. Unicode) стандарт кодирования символов, позволяющий представить знаки практически всех письменных языков. Стандарт предложен в 1991 году некоммерческой организацией «Консорциум Юникода» (англ. Unicode Consortium,… … Википедия
Математические обозначения — Список используемых в математике специфических символов можно увидеть в статье Таблица математических символов Математические обозначения («язык математики») сложная графическая система обозначений, служащая для изложения абстрактных… … Википедия
Знак плюс-минус — У этого термина существуют и другие значения, см. Плюс минус (значения). ± ∓ Знак плюс минус (±) математический символ, который ставится перед некоторым выражением и означает, что значение этого выражения может быть как положительным, так и … Википедия
Список обозначений в физике — Необходимо проверить качество перевода и привести статью в соответствие со стилистическими правилами Википедии. Вы можете помочь … Википедия
Знаки операций — или математические символы знаки, которые символизируют определённые математические действия со своими аргументами. К самым распространённым относятся: Плюс: + Минус: , − Знак умножения: ×, ∙ Знак деления: :, ∕, ÷ Знак возведения в… … Википедия
Знаки опеций — Знаки операций или математические символы знаки, которые символизируют определённые математические действия со своими аргументами. К самым распространённым относятся: Плюс: + Минус: , − Знак умножения: ×, ∙ Знак деления: :, ∕, ÷ Знак возведения… … Википедия
Знаки операторов — Знаки операций или математические символы знаки, которые символизируют определённые математические действия со своими аргументами. К самым распространённым относятся: Плюс: + Минус: , − Знак умножения: ×, ∙ Знак деления: :, ∕, ÷ Знак возведения… … Википедия
Оцените статью: Поделитесь с друзьями!Больше либо равно в ворде
Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как знак больше и знак меньше, а также знак равно.
Однако, если с последним что-то напутать достаточно сложно, то о том, как и в какую сторону пишутся знаки больше и меньше (знак менее и знак более, как ещё их иногда называют) многие сразу после этой же школьной скамьи и забывают, т.к. они довольно редко используются нами в повседневной жизни.
Но практически каждому рано или поздно всё равно приходится столкнуться с ними, и «вспомнить» в какую сторону пишется нужный им символ получается лишь обратившись за помощью к любимой поисковой системе. Так почему бы не ответить развернуто на этот вопрос, заодно подсказав посетителям нашего сайта как запомнить правильное написание этих знаков на будущее?
Именно о том, как правильно пишется знак больше и знак меньше мы и хотим напомнить вам в этой небольшой заметке. Также будет не лишним рассказать и том, как набрать на клавиатуре знаки больше или равно и меньше или равно, т.к. этот вопрос тоже довольно часто вызывает затруднения у пользователей, сталкивающихся с такой задачей очень редко.
Содержание:
Перейдем сразу к делу. Если вам не очень интересно запоминать всё это на будущее и проще в следующий раз снова «погуглить», а сейчас просто нужен ответ на вопрос «в какую сторону писать знак», тогда для вас мы приготовили краткий ответ — знаки больше и меньше пишутся так, как показано на изображении ниже.
А теперь расскажем немного подробнее о том, как это понять и запомнить на будущее.
Как и в какую сторону пишется знак больше
В общем и целом логика понимания очень проста — какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону — такой и знак. Соответственно, знак больше влево смотрит широкой стороной — большей.
Пример использования знака больше:
- 50>10 — число 50 больше числа 10;
- посещаемость студента в этом семестре составила >90% занятий.
Как и в какую сторону пишется знак меньше
Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной — меньшей, то перед вами знак меньше.
Пример использования знака меньше:
- 100 =», что, в принципе, часто вполне допустимо, но можно сделать красивее и правильнее.
На самом деле для того, чтобы напечатать эти знаки, существуют специальные символы, которые можно ввести на любой клавиатуре. Согласитесь, знаки «≤» и «≥» выглядят значительно лучше.
Знак больше или равно на клавиатуре
Для того, чтобы написать «больше или равно» на клавиатуре одним знаком даже не нужно лезть в таблицу специальных символов — просто поставьте знак больше с зажатой клавишей «alt». Таким образом сочетание клавиш (вводится в английской раскладке) будет следующим.
Или же вы можете просто скопировать значок из этой статьи, если вам нужно воспользоваться им один раз. Вот он, пожалуйста.
Знак меньше или равно на клавиатуре
Как вы наверное уже смогли догадаться сами, написать «меньше или равно» на клавиатуре вы можете по аналогии со знаком больше — просто поставьте знак меньше с зажатой клавишей «alt». Сочетание клавиш, которое нужно вводить в английской раскладке, будет следующим.
Или просто скопируйте его с этой страницы, если вам так будет проще, вот он.
Как видите, правило написания знаков больше и меньше довольно просто запомнить, а для того чтобы набрать значки больше или равно и меньше или равно на клавиатуре достаточно просто нажать дополнительную клавишу — всё просто.
В Word можно вставлять математические символы в уравнения и текст.
На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.
В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.
Щелкните стрелку рядом с названием набора символов и выберите набор символов, который вы хотите отобразить.
Щелкните нужный символ.
Доступные наборы символов
В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.
Основные математические символы
Часто используемые математические символы, такие как > и
Больше чем — объяснение и примеры
Что такое знак «больше»?
Знак «больше» — это математический символ, используемый для обозначения неравенства между двумя переменными или величинами. Этот знак используется с 1560-х годов. Знак обычно напоминает штрихи одинаковой длины, соединяющиеся острым углом (>).
Символ обычно помещается между двумя сравниваемыми величинами и обычно показывает, что первая переменная больше, чем вторая переменная.Знак «больше» используется в языках программирования для выполнения других операций.
Например, 2> 1 и 1> −2. Это означает, что 2 больше 1, а 1 больше отрицательных двух.
Вот некоторые из примеров, которые больше знака:
5> 2: Это неравенство показывает, что 5 больше 2
45> 30:45 больше 30
10/2> 6/3: Мы можем упростить это неравенство как 5> 2: что означает, что 5 больше 2
0.01> 0,001 означает, что 0,01 больше 0,001
2> -2: В этом случае очевидно, что положительные числа больше отрицательных. Следовательно, 2 больше, чем — 2.
Как запомнить знак «больше»?
Есть 3 способа запомнить знак «Больше».
Аллигаторный метод запоминания большего символа
Аллигаторный метод — самый простой метод запоминания большего чем символа. Всегда напоминайте себе об аллигаторе при сравнении переменных с помощью символа «больше».Пасть аллигатора всегда широко открыта, чтобы проглотить или проглотить как можно больше еды. Пасть аллигатора обычно открывается влево.
Метод запоминания символа «больше» с открытыми концами
Еще один простой способ вспомнить «большее» — это запомнить, что открытые концы знака обычно обращены к большему числу, а стрелка указывает на меньшее число.
L Метод
Напомним, что в этом методе меньшее, чем начинается с буквы L, напоминает символ «меньше», тогда как символ «больше» не похож на и знак, поэтому, поскольку знак «больше» не похож на букву L, не может быть «меньше чем».”
Решение проблем большего, чем
Перед тем, как пытаться решить любую проблему, имеющую отношение к символу больше чем, необходимо принять во внимание следующие соображения:
- Пройдите весь вопрос, чтобы понять его.
- Выделите ключевые слова, которые помогут в решении проблемы
- Определите переменные
- Напишите математическое выражение проблемы, используя символ неравенства.
- Обоснуйте выражение
Пример 1
Салех имеет 500 долларов на его сберегательном счете в конце года.К началу следующего года он намерен использовать на счету не менее 200 долларов. Если он еженедельно снимает 25 долларов, напишите выражение, описывающее эту ситуацию.
Решение
Начните с определения важных ключевых слов.
Допустим, переменные, и пусть w представляет количество недель
Следовательно, эта ситуация представлена следующим образом:
500 — 25w ≥ 200
В этой ситуации знак больше или равно использовался для обслуживания Сумма расходов должна составлять 200 долларов США.
Пример 2
У Брайана пятнадцать апельсинов, а у Филиппа девятнадцать апельсинов. Найдите человека, у которого есть еще апельсины.
Решение
Дано,
У Брайана 15 апельсинов.
У Филиппа 19 апельсинов.
Так как 19 больше 15, мы запишем неравенство как 19> 15
Следовательно, у Филиппа больше апельсинов, чем у Брайана.
Пример 3
Студент разрезал 20-метровую веревку на две части.Чем короче и длиннее кусок?
Решение
Пусть длина более короткого и более длинного отрезка равна y и x соответственно.
S и L должны быть больше нуля метров, а их сумма должна составлять 20 метров.
Запишите все неравенства:
- X> 0
- y> 0
- x <20
- y <20
- 0
- 0
- y
- 0
Теперь объединим выражения:
0 x + y = 20 м Из этих неравенств следует, что меньшая длина y больше нуля, а большая длина x больше y, а более длинная длина меньше общей 20 м.Точно так же сумма меньшей длины y и большей длины x эквивалентна 20 м. Меньше чем используется для описания отношения между двумя значениями. Он сообщает нам, что данная переменная меньше, больше или равна. Например, если дано 1 <3, это означает, что 1 меньше 3. Давайте узнаем, как определить, меньше ли число, а также важность символа «меньше чем» и как его использовать в деталях. Меньше чем — символ, примеры, значение
Что меньше?
Меньше чем означает, что одно значение меньше другого. Это термин, используемый для сравнения двух или более величин. Например, если мы хотим показать сравнение между 2 и 3, мы скажем, что 2 меньше 3 или 3 больше 2. Следовательно, оно отображает взаимосвязь между этими двумя числами. Мы можем показать эти числа как 2 <3.
Меньше символа
Посмотрите на символ ниже.
Этот знак в математике называется знаком «меньше». Это используется, чтобы показать, что одно значение меньше другого. Попробуем использовать это на примере. Если в утверждении говорится, что «16 меньше 18», это правда. Тогда мы можем записать это как 16 <18, используя знак «меньше». Широко открытая сторона знака с двумя точками всегда обращена к большему числу, тогда как меньшая конечная точка обращена к меньшему числу.
Когда использовать меньше?
Сравним двузначные числа 32 и 14.Сравнивая двузначные числа, мы сначала сравниваем цифры десятков. Если цифры десятков совпадают, мы будем сравнивать единицы.
Здесь мы видим, что 1 меньше 3. Таким образом, мы можем сказать, что 14 меньше 32. Математически мы можем записать это как 14 <32, используя знак «меньше». Ниже приведены еще несколько примеров, показывающих сравнение чисел с использованием знака «меньше».
| Символ | Пример | Значение |
|---|---|---|
| Менее < | а) 23 <32 б) 52 <78 в) 100> 85 | а) Число 23 меньше 32. б) Число 52 меньше 78. c) Число 85 меньше 100. |
Использование меньшего, чем в алгебре
В математике символы «меньше» и «больше» описывают неравенство между двумя значениями. Символ «<» используется для обозначения меньшего неравенства.
Важные примечания по менее чем
- Один из самых простых способов запомнить знаки «больше» и «меньше» — представить их голодными аллигаторами, которые всегда едят большее количество.Следовательно, широко открытая сторона знака обращена к большему числу.
- Другой способ запомнить их — заметить, что знак «<» похож на алфавит «L». Другими словами, «<» означает «Меньше чем».
☛Смежные статьи
Ниже приводится список тем, которые тесно связаны с менее чем. Эти темы также дадут вам представление о том, как такие концепции рассматриваются в Cuemath.
Часто задаваемые вопросы о менее чем
Что меньше, чем в математике?
Меньше, чем следует из названия, означает, что что-то меньше, чем по сравнению с другим количеством.Обозначается символом «<». Например, 2 <4 означает, что число 2 меньше числа 4.
Что означает «меньше или равно»?
Символ «меньше или равно» выглядит как « <». Открытая сторона символа должна быть перед большим значением. Подчеркнутый символ указывает на то, что значение может быть равным пределу или превышать его. Например, x < 7.
Здесь значение x должно быть равно или меньше 7.
Как объяснить «меньше или равно»?
Меньше или равно — это что-то меньшее или равное заданному количеству. Он также может быть выражен как минимум или минимум. Например, базовая зарплата женщин должна составлять 15 долларов или меньше 15 долларов, или мы можем сказать, что она должна быть меньше или равна 15 долларам.
В чем разница между меньшим и большим чем?
«Больше» означает, что некоторая переменная или число может иметь любое значение, которое больше заданного предела, не меньше этого или равно этому пределу, тогда как «меньше» означает, что число или переменная может быть меньше заданного предела. .Например, 8 больше 5. Мы можем представить это двумя разными способами, например, 8> 5 и 5 меньше 8 (5 <8).
В чем разница между «больше или равно» и «меньше или равно»?
Значение «больше или равно» указывает на то, что сумма должна быть больше или равна минимальному пределу, тогда как значение «меньше или равно» прямо противоположно значению «больше или равно». Меньше или равно означает, сумма должна быть равна или меньше максимального лимита.
4 меньше 3?
Нет, мы не можем сказать, что 4 меньше 3. Потому что 4 больше 3. Следовательно, правильным предложением будет 4 больше 3.
Какая польза от знака «Меньше чем»?
Знак «Меньше чем» используется, чтобы показать, что одна переменная меньше заданного количества. Например, 75 меньше 85. Это можно представить как 75 <85.
Может ли быть меньше, чем на числовой прямой?
Да, меньше, чем может быть представлено на числовой строке.Представление чисел в числовой строке позволяет легко определить, какие числа больше или меньше. Число слева меньше числа справа. Следовательно, все числа слева от 1 меньше 1.
Какое число меньше отрицательного?
В числовой строке отрицательные числа находятся слева от нуля. Наибольшее отрицательное целое число — -1. Не существует наименьшего отрицательного целого числа.
Меньше, чем Войти в математике | Что такое символ «меньше»? — Видео и стенограмма урока
Дополнительные проблемы приложений
Приложения по математике часто показываются с помощью текстовых задач.Многим ученикам сложно преобразовать слова в математику. В следующих примерах учащиеся будут практиковаться в преобразовании реальных ситуаций в неравенство, а затем будут решать его.
Примеры
1) Вы хотите купить несколько DVD-дисков на веб-сайте. Каждый DVD стоит 12 долларов, а доставка — 6,99 долларов. У вас есть 50 долларов, которые вы можете потратить. Напишите неравенство, отражающее ситуацию, и решите, сколько DVD-дисков вы можете купить.
2) Ваша любимая каша продается в продуктовом магазине за 2 доллара.25 шт. В коробке. Налог с продаж составляет 6,5%, а у вас есть 15 долларов США. Напишите неравенство, представляющее ситуацию, и решите, сколько коробок вы можете купить.
3) Стоимость аренды автомобиля составляет 50 долларов США плюс дополнительно 1,25 доллара США за каждую пройденную милю. Если вы хотите потратить менее 95 долларов на аренду, запишите неравенство и решите его, чтобы найти количество миль, которое вы можете проехать.
Решения
1) Если x обозначает количество DVD-дисков, которые вы можете купить, мы можем записать неравенство 12 x + 6.99 <50, что означает, что 12 долларов, умноженные на количество DVD, плюс стоимость доставки в размере 6,99 доллара должны быть меньше 50 долларов США. Чтобы решить неравенство, вычтите 6,99 из обеих частей и разделите на 12.
Таким образом, вы можете купить не более 3 DVD.
2) Если x обозначает количество коробок с хлопьями, мы можем написать 2,25 x + 0,065 * 2,25 x <15. Налог с продаж в размере 6,5% рассчитывается путем умножения стоимости x коробок. злаков на 0.065. Затем, упрощая и решая неравенство:
Таким образом, вы можете купить не более 6 коробок хлопьев.
3) Если x означает количество пройденных миль, то аренда автомобиля может быть представлена как 50 + 1,25 x <95. Решая это неравенство, мы имеем:
Таким образом, вы должны проехать менее 36 миль.
Общие математические символы и терминология
Математические символы и терминология могут сбивать с толку и мешать изучению и пониманию основ математики.
Эта страница дополняет наши страницы, посвященные навыкам счета, и предоставляет краткий глоссарий общих математических символов и терминологии с краткими определениями.
Мы что-то упускаем? Дайте нам знать.
Общие математические символы
+ сложение, плюс, положительное
Символ сложения + обычно используется для обозначения того, что два или более числа должны быть сложены вместе, например, 2 + 2.
Символ + также может использоваться для обозначения положительного числа, хотя он встречается реже, например, +2.На нашей странице о положительных и отрицательных числах объясняется, что число без знака считается положительным, поэтому плюс обычно не требуется.
См. Дополнительную информацию на нашей странице Дополнение .
— вычитание, минус, отрицательный
Этот символ имеет два основных применения в математике:
- — используется, когда нужно вычесть одно или несколько чисел, например, 2 — 2.
- Символ — также обычно используется для обозначения отрицательного или отрицательного числа, например −2.
См. Дополнительную информацию на нашей странице Вычитание .
× или * или. Умножение
Эти символы имеют то же значение; обычно × используется для обозначения умножения, когда написано от руки или используется на калькуляторе, например, 2 × 2.
Символ * используется в электронных таблицах и других компьютерных приложениях для обозначения умножения, хотя * имеет другие, более сложные значения в математике.
Реже умножение также может быть обозначено точкой. или вообще без символа. Например, если вы видите число, написанное вне скобок без оператора (символа или знака), то его следует умножить на содержимое скобок: 2 (3 + 2) совпадает с 2 × (3 + 2).
См. Дополнительную информацию на нашей странице Умножение .
÷ или / Подразделение
Оба эти символа используются для обозначения деления в математике.÷ обычно используется в рукописных вычислениях и на калькуляторах, например, 2 ÷ 2.
/ используется в электронных таблицах и других компьютерных приложениях.
Подробнее см. На нашей странице в Division .
= равно
Символ = равно используется, чтобы показать, что значения по обе стороны от него одинаковы. Чаще всего используется для отображения результата вычисления, например 2 + 2 = 4, или в уравнениях, например 2 + 3 = 10-5.
Вы также можете встретить другие похожие символы, но они встречаются реже:
- ≠ означает не равно. Например, 2 + 2 ≠ 5 — 2. В компьютерных приложениях (например, Excel) символы <> означают не равно.
- ≡ означает идентично. Это похоже на, но не совсем то же самое, что на равно. Поэтому, если сомневаетесь, придерживайтесь =.
- ≈ означает примерно равно или почти равно.Две стороны отношения, обозначенные этим символом, будут не достаточно точными для математических манипуляций.
<Меньше и> Больше
Этот символ < означает меньше, например 2 <4 означает, что 2 меньше 4.
Этот символ > означает больше, например, 4> 2.
≤ ≥ Эти символы означают «меньше или равно» и «больше или равно» и обычно используются в алгебре.В компьютерных приложениях используются <= и> =.
≪ ≫ Эти символы встречаются реже и означают намного меньше или намного больше.
± плюс или минус
Этот символ ± означает «плюс или минус». Он используется, например, для обозначения доверительных интервалов вокруг числа.
Говорят, что ответ — это «плюс-минус» другое число, или, другими словами, в пределах диапазона данного ответа.
Например, 5 ± 2 на практике может быть любым числом от 3 до 7.
∑ Сумма
Символ ∑ означает сумму.
∑ — заглавная греческая буква сигма. Он обычно используется в алгебраических функциях, и вы также можете заметить его в Excel — кнопка Автосумма имеет сигму в качестве значка.
° Степень
Градусы ° используются по-разному.
- Как мера поворота — угол между сторонами фигуры или поворот круга.Круг равен 360 °, а прямой угол — 90 °. См. Наш раздел о Geometry для получения дополнительной информации.
- Мера температуры. градусов Цельсия или Цельсия используются в большинстве стран мира (за исключением США). Вода замерзает при 0 ° C и закипает при 100 ° C. В США используется градус Фаренгейта. По шкале Фаренгейта вода замерзает при 32 ° F и закипает при 212 ° F. Смотрите нашу страницу: Системы измерения для получения дополнительной информации.
∠ Угол
Символ угла ∠ используется как сокращение в геометрии (изучении форм) для описания угла.
Выражение ∠ABC используется для описания угла в точке B (между точками A и C). Точно так же ∠BAC может использоваться для описания угла точки A (между точками B и C). Подробнее об углах и других геометрических терминах см. На наших страницах Геометрия .
√ Квадратный корень
√ — символ квадратного корня. Квадратный корень — это число, которое при умножении на себя дает исходное число.
Например, квадратный корень из 4 равен 2, потому что 2 x 2 = 4.Квадратный корень из 9 равен 3, потому что 3 x 3 = 9.
См. Нашу страницу: Специальные числа и понятия для получения дополнительной информации о квадратных корнях.
n Мощность
Целое число с верхним индексом (любое целое число n ) — это символ, используемый для обозначения степени числа.
Например, 3 2 означает 3 в степени 2, что совпадает с 3 в квадрате (3 x 3).
4 3 означает 4 в степени 3 или 4 в кубе, то есть 4 × 4 × 4.
См. Наши страницы Расчетная площадь и Расчет объема , где приведены примеры использования чисел в квадрате и кубе .
Степень также используется как сокращенный способ записи больших и малых чисел.
Большие числа
10 6 — 1 000 000 (один миллион).
10 9 — 1 000 000 000 (один миллиард).
10 12 — 1 000 000 000 000 (один триллион).6 = 10 6 = 1000000 (один миллион).
. Десятичная точка
. — символ десятичной точки, часто называемый просто «точкой». См. Нашу страницу Десятичные знаки для примеров его использования.
, Разделитель тысяч
Запятую можно использовать для разделения больших чисел и облегчения их чтения.
Тысячу можно записать как 1000, так и 1000, а миллион — как 1000000 или 1000000.Запятая разделяет большие числа на блоки по три цифры.
В большинстве англоязычных стран, не имеет математической функции, он просто используется для облегчения чтения чисел.
В некоторых других странах, особенно в Европе, запятая может использоваться вместо десятичной точки, и действительно, десятичная точка может использоваться вместо запятой в качестве визуального разделителя. Это объясняется более подробно на нашей странице Introduction to Numbers .
[], () Скобки, круглые скобки
Скобки () используются для определения порядка вычислений в соответствии с правилом BODMAS.
Сначала вычисляются части расчета, заключенные в скобки, например
- 5 + 3 × 2 = 11
- (5 + 3) × 2 = 16
% В процентах
Символ% означает процент или число из 100.
Узнайте все о процентах на нашей странице: Введение в проценты
π Pi
π или пи — греческий символ звука «п».Это часто встречается в математике и является математической константой. Пи — это длина окружности круга, деленная на ее диаметр, и имеет значение 3,141592653. Это иррациональное число, что означает, что его десятичные разряды продолжаются до бесконечности.
∞ Бесконечность
Символ ∞ означает бесконечность — понятие, согласно которому числа существуют вечно.
Каким бы большим у вас ни было число, у вас всегда может быть номер побольше, потому что вы всегда можете добавить к нему еще один.
Бесконечность — это не число, а идея чисел, существующая вечно. Вы не можете прибавить единицу к бесконечности, как нельзя прибавить единицу к человеку, полюбить или ненавидеть.
\ (\ bar x \) (x-bar) Среднее значение
\ (\ bar x \) — среднее всех возможных значений x.
Чаще всего этот символ встречается в статистике.
См. Нашу страницу на Среднее значение для получения дополнительной информации.
! Факториал
! это символ факториала.
н! — произведение (умножение) всех чисел от n до 1 включительно, т.е. n × (n − 1) × (n − 2) ×… × 2 × 1.
Например:
5! = 5 × 4 × 3 × 2 × 1 = 120
10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3,628,800
| Труба
Труба ‘|’ также называется вертикальной чертой, vbar, pike и имеет множество применений в математике, физике и вычислениях.
Чаще всего в базовой математике он используется для обозначения абсолютного значения или модуля действительного числа, где \ (\ vert x \ vert \) — это абсолютное значение или модуль \ (x \) .
Математически это определяется как
$$ \ vert x \ vert = \ biggl \ {\ begin {eqnarray} -x, x \ lt 0 \\ x, x \ ge 0 \ end {eqnarray} $$
Проще говоря, \ (\ vert x \ vert \) — неотрицательное значение \ (x \). Например, модуль 6 равен 6, а модуль −6 также равен 6.
Он также используется в вероятности, где P (Z | Y) обозначает вероятность X с учетом Y.
∝ Пропорциональный
∝ означает «пропорционально » и используется, чтобы показать что-то, что меняется по отношению к чему-то другому.
Например, если x = 2y, то x ∝ y.
∴ Следовательно
∴ — удобная сокращенная форма слова «поэтому», используемая в математике и естественных науках.
∵ Потому что
∵ — удобная сокращенная форма слова «потому что», не путать с «поэтому».
Математическая терминология (A-Z)
Амплитуда
Когда объект или точка движется циклически, или подвергается вибрации или колебаниям (например,грамм. маятник), амплитуда — это максимальное расстояние, на которое он перемещается от своей центральной точки. См. Введение в геометрию для получения дополнительной информации.
Апофема
Линия, соединяющая центр правильного многоугольника с одной из его сторон. Линия перпендикулярна (под прямым углом) в сторону.
Площадь
Геометрическая площадь определяется как пространство, занимаемое плоской формой или поверхностью объекта. Площадь измеряется в квадратных единицах, например в квадратных метрах ( м 2 ).Для получения дополнительной информации см. Нашу страницу о площади , площади поверхности и объеме .
Асимптота
Асимптота — это прямая линия или ось, которая конкретно связана с изогнутой линией. По мере того, как кривая линия расширяется (стремится) к бесконечности, она приближается к своей асимптоте (то есть расстояние между кривой и асимптотой стремится к нулю, но никогда не касается ее). Встречается в геометрии и тригонометрии .
ось
Контрольная линия, вокруг которой нарисован, повернут или измерен объект, точка или линия.В симметричной форме ось обычно представляет собой линию симметрии.
Коэффициент
Коэффициент — это число или величина, умножающая другую величину. Обычно его ставят перед переменной . В выражении 6 x 6 — коэффициент, а x — переменная.
Окружность
Окружность — это длина расстояния по краю круга. Это тип с периметром , который уникален для круглых форм.Для получения дополнительной информации см. Нашу страницу о изогнутых форм .
Данные
Данные представляют собой набор значений, информации или характеристик, которые часто имеют числовой характер. Они могут быть собраны с помощью научного эксперимента или других средств наблюдения. Это могут быть количественных или качественных переменных. Датум — это отдельное значение одной переменной. См. Нашу страницу Типы данных для получения дополнительной информации.
Диаметр
Диаметр — это термин, используемый в геометрии для обозначения прямой линии, которая проходит через центр круга или сферы, касаясь окружности или поверхности с обоих концов.Диаметр в два раза больше радиуса .
Экстраполировать
Экстраполяция — это термин, используемый при анализе данных. Это относится к расширению графика, кривой или диапазона значений в диапазон, для которого нет данных, с выводом значений неизвестных данных из тенденций в известных данных.
Фактор
Коэффициент — это число, которое мы умножаем на другое число. Фактор делится на другое число целое число раз. У большинства чисел есть четное количество факторов.Квадратное число имеет нечетное количество множителей. Простое число имеет два множителя — само себя и 1. Простой множитель — множитель, который является простым числом. Например, простые множители 21 равны 3 и 7 (потому что 3 × 7 = 21, а 3 и 7 — простые числа).
Среднее значение, медиана и мода
Среднее значение (среднее значение) набора данных вычисляется путем сложения всех чисел в наборе данных и последующего деления на количество значений в наборе.Когда набор данных упорядочен от наименьшего к наибольшему, медиана является средним значением. Режим — это число, которое встречается чаще всего.
Операция
Математическая операция — это шаг или этап в вычислении, или математическое «действие». Основные арифметические операции — сложение, вычитание, умножение и деление. Порядок, в котором выполняются операции при вычислении, важен. Порядок операций известен как BODMAS .
Математические операции часто называют «суммами». Строго говоря, «сумма» — это операция сложения. В SYN мы имеем в виду операции и вычисления, но в повседневной речи вы часто можете услышать общий термин «суммы», который неверен.
Периметр
Периметр двумерной фигуры — это непрерывная линия (или длина линии), определяющая контур фигуры. Периметр круглой формы называется ее окружностью .Наша страница по периметру объясняет это более подробно.
Пропорции
Пропорция — это относительное отношение. Соотношения сравнивают одну часть с другой, а пропорции сравнивают одну часть с целым. Например, «3 из 10 взрослых в Англии имеют избыточный вес». Пропорция относится к дробям .
Пифагор
Пифагор был греческим философом, которому приписывают ряд важных математических и научных открытий, возможно, наиболее значительное из которых стало известно как Теорема Пифагора .
Это важное правило применяется только к прямоугольным треугольникам. В нем говорится, что «квадрат гипотенузы равен сумме квадратов на двух других сторонах».
Количественный и качественный
Количественные данные — это числовые переменные или значения, которые могут быть выражены численно, то есть сколько, сколько, как часто, и получаются путем подсчета или измерения.
Качественные данные — это переменные типа, которые не имеют числового значения и могут быть выражены описательно, т.е.е. с использованием имени или символа и получаются путем наблюдения.
Подробнее см. Нашу страницу о типах данных .
Радиан
Радиан — это единица СИ для измерения углов. Один радиан эквивалентен углу, образуемому в центре круга дугой, равной по длине радиусу. Один радиан чуть меньше 57,3 градуса. Полный оборот (360 градусов) составляет 2π радиан.
Радиус
Термин радиус используется в контексте кругов и других изогнутых форм.Это расстояние от центральной точки круга, сферы или дуги до ее внешнего края, поверхности или окружности . Диаметр в два раза больше радиуса. Для получения дополнительной информации см. Нашу страницу о изогнутых форм .
Диапазон
В статистике диапазон данного набора данных — это разница между наибольшим и наименьшим значениями.
Коэффициент
Коэффициент— это математический термин, используемый для сравнения размеров одной детали с другой.Соотношения обычно отображаются в виде двух или более чисел, разделенных двоеточием, например, 7: 5, 1: 8 или 5: 2: 1.
Стандартное отклонение
Стандартное отклонение набора данных измеряет, насколько данные отличаются от среднего значения, то есть это мера вариации или разброса набора значений. Если разброс данных невелик и все значения близки к среднему, стандартное отклонение будет низким. Высокое стандартное отклонение указывает на то, что данные распределены в более широком диапазоне
Срок
Термин — это отдельное математическое выражение.Это может быть одно число, одна переменная (например, x ) или несколько констант и переменных, умноженных вместе (например, 3 x 2). Термины обычно разделяются операциями сложения или вычитания. Термин может включать операции сложения или вычитания, но только в скобках, например 3 (2 -x3).
переменная
Переменная — это коэффициент в математическом выражении, арифметическом соотношении или научном эксперименте, который может изменяться.В эксперименте обычно используются три типа переменных: независимые, зависимые и контролируемые. В выражении 6 x , 6 — это коэффициент , а x — переменная.
Разница
Дисперсия — это статистическое измерение, которое указывает разброс между элементами в наборе данных. Он измеряет, насколько далеко каждый член в наборе находится от среднего и, следовательно, от каждого другого члена в наборе.
Вектор
Векторы описывают математические величины, которые имеют как величину, так и направление.Векторы встречаются во многих математических и физических приложениях, например изучение движения, где скорость, ускорение, сила, смещение и импульс являются векторными величинами.
Объем
Объем — это трехмерное пространство, занимаемое твердой или полой формой. Он измеряется кубическими размерами пространства, ограниченного его поверхностями. Объем измеряется в кубических единицах, например м 3 .
Дополнительная литература по навыкам, которые вам нужны
Руководство по навыкам, которые вам нужны
Это руководство из четырех частей познакомит вас с основами математики от арифметики до алгебры с остановками на дробях, десятичных дробях, геометрии и статистике.
Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.
Что больше? [Определение, факты и пример]
Greater Than Games
Сравните числаСравните два целых числа до миллиона. Начните с использования диаграмм значений и числовых линий для сравнения, прежде чем переходить к прямому сравнению.
охватывает Common Core Curriculum 4.NBT.2Играть сейчасПосмотреть все игры с ощущением чисел >>Учитесь с помощью полной программы обучения математике K-5
Что больше?Больше, чем можно определить как неравенство, используемое для сравнения двух или более чисел, количеств или значений.
Используется, когда количество или число больше или больше второго или остальных количеств или чисел.
Символ> используется для сравнения чисел и значений. Широкая открытая сторона знака всегда обращена к большему числу, а маленький конец указывает на меньшее число.
Здесь 8 больше 5.
Иногда значения также могут быть «больше или равны».Например, сравнивая количество воды, которое могут вместить два контейнера, мы можем сказать, что вместимость контейнеров больше или равна 5 чашкам.
Мы используем знак ≥ для обозначения «больше или равно», причем большее количество находится на широко открытой стороне символа.
Интересные факты
|
Давайте споем!
При сравнении цифр и сомневаюсь,
Подумайте о широко раскрытой морде мистера Аллигатора.
От больших сочных цифр рот широко раскрывается.
Маленькие цифры заставляют его повернуться в сторону.
Давайте сделаем это!
Вместо того, чтобы раздавать своим детям листы сравнения, попросите их сравнить количества, которые вы им показываете.Покажите им разные вещи, например, полный стакан молока и полстакана молока, банку, наполовину заполненную печеньем, и банку, полную чипсов, 20 мелков и 12 карандашей.
Попросите их провести воздушную трассировку символа, чтобы показать, какое количество больше, и используйте «больше чем» при изложении своих наблюдений.
Связанный математический словарь
Менее.
| NOOKS AND CRANNIES Как правильно назвать этот символ> Джуди, Беттсвилл, США
|
Знаки больше и меньше: как их запомнить
В математике, экономике, физике или других предметах, связанных с вычислениями, вы, должно быть, встречали символы в каратах, расположенные сбоку. Что именно они означают? Эти маленькие знаки — символы неравенства. Но самое примечательное в них то, что учащимся их очень трудно запомнить, потому что они кажутся похожими.Примечательно, что символы равенства являются одними из самых важных знаков, поскольку они помогают продемонстрировать взаимосвязь между уравнениями и числами.
В этом посте мы собираемся глубже изучить знаки, которые больше, чем меньше, чтобы прояснить, как они работают, и помочь вам их запомнить.
Что означает символы «больше» и «меньше»?
Два знака используются для сравнения двух вещей. В математических задачах знаки неравенства не помогают их решить (вы не получите внятного ответа).Скорее, они показывают, как одно число связано с другим, указывая, что оно больше или меньше. Итак, вы можете сказать одно, когда
| Символ | Символ, означающий |
| Этот символ означает меньше. Это означает, что число слева меньше, чем справа. Например, 4 | |
| > | Этот символ означает больше чем.Это означает, что число слева больше, чем справа. Вот пример; 10> 9. |
| ≤ | Этот символ означает, что указанное число меньше или равно значению слева. Вот пример; 4 или 5 ≤ 4. |
| ≥ | Этот знак означает, что число справа больше или равно числу слева. Например, 5 или 6 ≥ 5. |
| ≠ | Этот символ просто означает, что не равно.Число слева не равно числу справа. Пример, 4 ≠ 5. |
Секрет запоминания
Теперь, когда мы продемонстрировали, что означает «меньше чем больше или равно», мы обратимся к методам, которые вы можете использовать для их запоминания.
Это один из рекомендуемых вариантов, который поможет вам легко запомнить символы «меньше» и «больше». Что ж, вы просто принимаете символы как аллигаторы, а числа с обеих сторон — это количество рыб.Поскольку аллигатор всегда пытается съесть рыбу, число, которому открыт рот, всегда больше, чем.
В приведенном выше примере пасть аллигатора открыта на пятерых. Следовательно, пять больше четырех. Этот метод также может помочь вам узнать о другом номере. Если пять больше четырех, это означает, что четыре меньше пяти.
В этом случае рассмотрите пять как пасть маленького аллигатора, который собирается поймать и съесть немного рыбы.Поскольку рот направлен в сторону восьми, это означает, что восемь больше пяти. Знак всегда расскажет, как связаны эти два числа. Итак, если восемь больше пяти, это означает, что пять также меньше восьми.
Чтобы запоминать больше, чем меньше знаков, проявите творческий подход. Идите вперед и настройте аллигатора. Например, добавьте несколько глаз, чтобы указать, куда смотрит аллигатор.
Если вы возьмете знак «меньше» и немного повернетесь, что вы получите? Знак L. Этот трюк довольно прост; просто скажите своему разуму, что символ меньше чем начинается с буквы L.Следовательно, знак, похожий на знак L, должен означать меньше, чем. Например, поскольку> не похож на L, он не может быть меньше. Однако
- Запоминание знака равенства
Как только вы усвоите концепции метода L и метода Аллигатора, все станет проще. Знаки «равно» или «меньше» и «равно» просто содержат под ними символ половины равенства. Возьмем, к примеру, 5 или 6 ≥ 2. Это уравнение имеет больший знак, но также имеет половинный знак равенства.Следовательно, это означает, что пять или шесть больше или равны двум.
Если по-другому, то тоже будет правда. Однако ситуация будет меньше или равна типу отношений.
Когда вы используете знак «не равно», запоминать его еще проще. Вы просто проверяете перечеркнутый знак равенства. Возьмем пример 2 ≠ 4. В этом случае это просто означает, что два не равно четырем. Число слева не равно числу справа.
Уловки, которые следует использовать при работе со знаками «меньше чем» и «больше»
Примечательно, что многие неравенства могут быть сложными, потому что вы не решите однозначного ответа. Таким образом, с ними будет легче работать, если помнить о следующем:
- Неравенства используются для демонстрации взаимосвязей.
- Всегда изолируйте переменные, с которыми вы работаете, чтобы знать, какая из них больше, меньше, равна или не равна.
- Когда вы используете отрицательные числа, эффект меняет больший или меньший знаки.
- В большинстве случаев избегайте умножения или деления на переменную.
Теперь вы знаете меньше и больше, чем знак… Что дальше?
В этом посте мы продемонстрировали знаки «меньше и больше». Итак, следующее — применить их в своей учебе. Постарайтесь определить признаки и решить связанные с ними проблемы. Это должно быть легко, правда? Но если вам все еще сложно, не тратьте время, думая, что домашнее задание слишком сложно для вас и должно быть запрещено — пора обратиться за помощью к профессиональному писателю.
Рассмотрите возможность работы с профессиональными писателями, потому что они понимают все концепции математики и готовы помочь.