Математические знаки ≈ ∑ ⇒ ∈ ≤ ∞
В разделе собраны математические символы, которые невозможно корректно отобразить с помощью ввода на клавиатуре. Весь представленный набор можно разделить на несколько групп:
- знаки операций – сложение, вычитание, деление, умножение, сумма, тождество;
- символы интегралов – двойные, тройные, интеграл по объему, поверхности, с правым и левым обходом;
- знаки сравнения – больше, меньше, равно;
- геометрические символы – отображение угла, пропорции, диаметра;
- геометрические фигуры;
- знак извлечения из корня, степень;
- иные символы – бесконечность, множество, квантор существования.
Использование данных иконок – единственный вариант корректного отображения ряда математических символов на сайте или в сообщении в любой операционной системе конечного пользователя. Достаточно лишь скопировать закодированный значок. Применение изображений для этих целей значительно усложняет процесс, требует подгонки при разработке и наполнении интернет-ресурса. Кроме того, медиа-контент занимает большой объем дискового пространства.
Математические символы подойдут для публикаций в социальных сетях, создания сообщений в чатах и форумах, разработки интернет-страниц.
Математика, как язык всех наук, не может обходиться без системы записи. Многочисленные понятия, и операторы обрели своё начертание по мере развития этой науки. Так как в стандартные алфавиты эти символы не входят, напечатать их с клавиатуры может оказаться проблематично. Отсюда можно скопировать и вставить.
Консорциуму Юникода не чужды проблемы учёных, поэтому в таблицу было включено множество различных знаков. Если тут нет того, что нужно, воспользуйтесь поиском по сайту или посмотрите в разделах математические символы, разнообразные математические символы-A, разнообразные математические символы-B, дополнительные математические операторы. Буквы для формул можно взять в наборе греческие буквы и блоке математические буквенно-цифровые символы.
Числа для степеней составляются из маленьких цифр. Там же собраны дроби.
| Символ (TeX) | Символ (Unicode) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒ → ⊃ | Импликация, следование | означает «если верно, то также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже. (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). | верно, но неверно (так как также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает « верно тогда и только тогда, когда верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда и оба истинны. | , если — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий и истинно. | , если — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| ¬ | Отрицание | истинно тогда и только тогда, когда ложно . | ||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает « верно для всех ». | ||
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один такой, что верно » | (подходит число 5) | |
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | обозначает « и обозначают одно и то же значение». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| := :⇔ | Определение | означает « по определению равен ». означает « по определению равносильно » | (Гиперболический косинус) (Исключающее или) | |
| «равно/равносильно по определению» | ||||
| везде | ||||
| { , } | Множество элементов | означает множество, элементами которого являются , и . | (множество натуральных чисел) | |
| «Множество…» | ||||
| Теория множеств | ||||
| { | } { : } | Множество элементов, удовлетворяющих условию | означает множество всех таких, что верно . | ||
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅ {} | Пустое множество | и означают множество, не содержащее ни одного элемента. | ||
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈ ∉ | Принадлежность/непринадлежность к множеству | означает « является элементом множества » означает « не является элементом множества » | ||
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆ ⊂ | Подмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇ ⊃ | Надмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋ | Собственное надмножество | означает и . | ||
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪ | Объединение | означает множество элементов, принадлежащих или (или обоим сразу). | ||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| Пересечение | означает множество элементов, принадлежащих и , и . | |||
| «Пересечение … и … », «…, пересечённое с …» | ||||
| Теория множеств | ||||
| \ | Разность множеств | означает множество элементов, принадлежащих , но не принадлежащих . | ||
| «разность … и … », «минус», «… без …» | ||||
| Теория множеств | ||||
| → | Функция | означает функцию с областью определения и областью прибытия (областью значений) . | Функция , определённая как | |
| «из … в», | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом после применения функции будет . | Функцию, определённую как , можно записать так: | |
| «отображается в» | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или реже (в зависимости от ситуации). | ||
| «Эн» | ||||
| Числа | ||||
| Z или ℤ | Целые числа | означает множество | ||
| «Зед» | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| «Ку» | ||||
| Числа | ||||
| R или ℝ | Вещественные числа, или действительные числа | означает множество всех пределов последовательностей из | ( — комплексное число: ) | |
| «Эр» | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| «Це» | ||||
| Числа | ||||
| < > | Сравнение | обозначает, что строго меньше . означает, что строго больше . | ||
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| ≤ или ⩽ ≥ или ⩾ | Сравнение | означает, что меньше или равен . означает, что больше или равен . | ||
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до означает, что 2,718 отличается от не больше чем на . | с точностью до . | |
| «приблизительно равно» | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает неотрицательное действительное число, которое в квадрате даёт . | ||
| «Корень квадратный из …» | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов . | ||
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма, сумма ряда | означает «сумма , где принимает значения от 1 до », то есть . означает сумму ряда, состоящего из . | ||
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает «произведение для всех от 1 до », то есть | ||
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| ! | Факториал | означает «произведение всех натуральных чисел от 1 до включительно, то есть | ||
| « факториал» | ||||
| Комбинаторика | ||||
| ∫ | Интеграл | означает «интеграл от до функции от по переменной ». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
| df/dx f'(x) | Производная | или означает «(первая) производная функции от по переменной ». | ||
| «Производная … по …» | ||||
| Математический анализ | ||||
| Производная -го порядка | или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ». | |||
| «-я производная … по …» | ||||
| Математический анализ |
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Алфавиты, номиналы, единицы / / Алфавиты, в т.ч. греческий и латинский. Символы. Коды. Альфа, бета, гамма, дельта, эпсилон… / / Таблица научных, математических, физических символов и сокращений. Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит. Поделиться:
| ||||
Знак (математика) — Википедия
- Это статья о понятии положительности и отрицательности. О математических символах см. таблицу математических символов. О других значениях термина см. Знак.

Знак вещественного числа в арифметике позволяет отличить отрицательные числа от положительных; традиционно знак обозначается символом плюса (положительные числа) или минуса (отрицательные) перед записью числа. Если ни плюс, ни минус не указаны, число считается положительным. Ноль как особое число не имеет знака.
Примеры записи чисел: +36,6; −273; 142.{\displaystyle +36{,}6;\ {-}273;\ 142.} Последнее число не имеет знака и поэтому положительно.
Следует отметить, что плюс и минус указывают знак для чисел, но не для буквенных переменных или алгебраических выражений. Например, в формулах −t; a+b; −(a2+b2){\displaystyle -t;\ a+b;\ -(a^{2}+b^{2})} символы плюса и минуса задают не знак выражения, перед которым они стоят, а знак арифметической операции, так что знак результата может быть любым, он определяется только после вычисления выражения.
Кроме арифметики, понятие знака используется в других разделах математики, в том числе для нечисловых математических объектов (см. ниже). Понятие знака важно также в тех разделах физики, где физические величины делятся на два класса, условно названные положительными и отрицательными — например, электрические заряды, положительная и отрицательная обратная связь, разнообразные силы притяжения и отталкивания.
Положительные и отрицательные числа[править | править код]

Вещественное число называется положительным, если оно больше нуля, и отрицательным, если меньше. Положительные числа записываются со знаком плюс или вообще без знака, отрицательные — со знаком минус[1].
Нулю не присвоен никакой знак, то есть +0{\displaystyle +0} и −0{\displaystyle -0} — это в арифметике одно и то же число[1]. В математическом анализе смысл символов +0{\displaystyle +0} и −0{\displaystyle -0} может различаться, см. об этом Отрицательный и положительный ноль; в информатике компьютерная кодировка двух нулей (целого типа) может отличаться, см. Прямой код.
В связи со сказанным вводятся ещё несколько полезных терминов:
- Число неотрицательно, если оно больше или равно нулю.
- Число неположительно, если оно меньше или равно нулю.
- Положительные числа без нуля и отрицательные числа без нуля иногда (чтобы подчеркнуть, что они ненулевые) называют «‘строго положительными» и «строго отрицательными» соответственно.
Та же терминология иногда используется для вещественных функций. Например, функция называется положительной, если все её значения положительны, неотрицательной, если все её значения неотрицательны и т. д. Говорят также, что функция положительна/отрицательна на заданном интервале её определения..
Для комплексных чисел понятия знака числа не существует, потому что для них не определено, как сравнивать числа на больше/меньше.
Функция знака sgn(x)[править | править код]
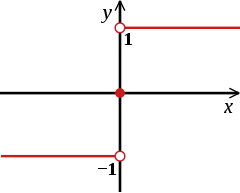 График функции y=sgn(x){\displaystyle y=\operatorname {sgn}(x)}
Основная статья: sgn
График функции y=sgn(x){\displaystyle y=\operatorname {sgn}(x)}
Основная статья: sgnФункция знака y=sgn(x){\displaystyle y=\operatorname {sgn}(x)} (произносится: сигнум от x) часто бывает полезна как индикатор знака числа. Эта функция определяется следующим образом:
- sgn(x)={−1(x<0), 0(x=0), 1(x>0).{\displaystyle \operatorname {sgn}(x)={\begin{cases}-1\quad (x<0),\\~~\,0\quad (x=0),\\~~\,1\quad (x>0).\end{cases}}}
Другими словами, функция равна 1{\displaystyle 1} для положительного аргумента, −1{\displaystyle -1} для отрицательного и нулю для нулевого аргумента. Функция предусмотрена и в ряде языков программирования.
Пример использования функции см. в статье Квадратный корень#Комплексные числа.
Модуль (абсолютная величина) числа[править | править код]
Если у числа x{\displaystyle x} отбросить знак, полученное значение называется модулем или абсолютной величиной числа x{\displaystyle x}, оно обозначается |x|.{\displaystyle |x|.} Примеры: |3|=3; |−3|=3.{\displaystyle |3|=3;\ |{-3}|=3.}
Для любых вещественных чисел a,b{\displaystyle a,b} имеют место следующие свойства.
Знак угла[править | править код]
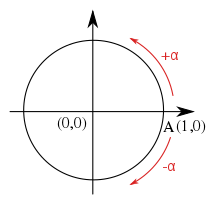 Положительные и отрицательные углы
Положительные и отрицательные углыВеличина угла на плоскости считается положительной, если она измеряется против часовой стрелки, иначе — отрицательной. Аналогично классифицируются два случая вращения:
- вращение на плоскости — например, вращение на (–90°) происходит по часовой стрелке;
- поворот в пространстве вокруг ориентированной оси, как правило, считается положительным, если выполнено «правило буравчика», иначе он считается отрицательным.
Знак направления[править | править код]
В аналитической геометрии и физике нередко продвижения вдоль заданной прямой или кривой условно делятся на положительные и отрицательные. Такое деление может зависеть от постановки задачи или от выбранной системы координат. Например, при подсчёте длины дуги кривой часто удобно приписать этой длине на одном из двух возможных направлений знак минус.
Знак в вычислительной технике[править | править код]
| старший бит | |||||||||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | 127 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | 126 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | = | 2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | −1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | −2 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | −127 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | −128 |
| Для представления знака целого числа большинство компьютеров используют дополнительный код. | |||||||||
Целое число, хранящееся в памяти компьютера, может быть знаковым или беззнаковым (в последнем случае оно рассматривается как положительное). Знаковые числа используют один из битов как код знака (обычно 0 кодирует положительное число, 1 — отрицательное), у беззнаковых все биты равноправны. Для представления знака и значения целых чисел большинство компьютеров используют дополнительный код, хотя встречается и прямой код.
Вещественные числа хранятся и обрабатываются как числа с плавающей запятой, то есть содержат мантиссу и порядок числа, причём каждая из этих частей снабжена битом своего знака.
Дискретная математика[править | править код]
В комбинаторике определяется знак перестановки — положительный, если перестановка чётная, и отрицательный, если перестановка нечётная.
В теории графов рассматриваются ориентированные и знаковые графы[en], в которых каждому ребру соответствует направление или знак (положительный или отрицательный).
Другие применения знака[править | править код]
Существует знако-разрядная система счисления[en], в ней каждая цифра числа может иметь положительный или отрицательный знак..
В теории меры определено понятие обобщённой меры со знаком («заряда»), которая может иметь положительные или отрицательные значения.
Знак может быть присвоен бесконечно удалённой точке расширенной числовой оси.
В физике, любой электрический заряд обладает знаком, положительным или отрицательным. По соглашению, положительным считается заряд с тем же знаком, что у протона, а отрицательный заряд — это заряд с тем же знаком, что у электрона.
Знак равенства — Википедия
Материал из Википедии — свободной энциклопедии
Символы со сходным начертанием: 二 · ニ · ═ · ꞊| Знак равенства | |
|---|---|
| = | |
Изображение
| |
| equals sign | |
| Юникод | U+003D |
| HTML-код | |
| UTF-16 | 0x3D |
| %3D | |
Знак равенства (=) в математике, в логике и других точных науках — символ, который пишется между двумя идентичными по своему значению выражениями.
Знак равенства в современной форме создал математик Роберт Рекорд (Robert Recorde, 1510—1558) в своём труде The Whetstone of Witte (1557). Он обосновал применение двух параллельных штрихов так (орфография оригинала — ранненовоанглийский): «…bicause noe 2 thynges can be moare equalle», то есть «никакие другие две вещи не могут быть более равными». До этого в античной и средневековой математике равенство обозначалось словесно (например est egale). Рене Декарт в XVII веке при записи стал использовать æ (от лат. aequalis), а современный знак равенства он использовал, чтобы указать, что коэффициент может быть отрицательным. Франсуа Виет знаком равенства обозначал вычитание. Символ Рекорда получил распространение далеко не сразу. В континентальной Европе знак «=» был введён Лейбницем только на рубеже XVII—XVIII веков, то есть более чем через 100 лет после смерти впервые использовавшего его для этого Роберта Рекорда.
Таблица математических знаков (символов) эквивалентности с кодами Unicode[править | править код]
 | Необходимо добавить символы: |
В языках программирования символ = чаще всего используется для операций сравнения и/или присваивания. В некоторых языках (например, Basic) символ используется для обеих операций, в зависимости от контекста. В языках C, PHP и т. п. = обозначает присваивание, равенство записывается как ==. В Perl, кроме того, операторы для сравнения строк отличаются от операторов для сравнения чисел, равенство строк проверяет eq. В Pascal, напротив, = обозначает равенство, присваивание обозначается :=.
| |
| Символ (TeX) | Символ (Unicode) | Назва | Значення | Приклад |
|---|---|---|---|---|
| Вимова | ||||
| Розділ математики | ||||
| ⇒{\displaystyle \Rightarrow \,} | ⇒ | Імплікація, слідування | A⇒B{\displaystyle A\Rightarrow B\,} означає «коли A{\displaystyle A} істинне, то B{\displaystyle B} також істинне». Іноді використовують →{\displaystyle \rightarrow \,}. | x=2⇒x2=4{\displaystyle x=2\Rightarrow x^{2}=4\,} істинне, але x2=4⇒x=2{\displaystyle x^{2}=4\Rightarrow x=2\,} хибно (тому що x=−2{\displaystyle x=-2} також є розв’язком). |
| «з… випливає» або «якщо…, то…» | ||||
| скрізь | ||||
| ⇔{\displaystyle \Leftrightarrow } | ⇔, ↔ | Рівносильність | A⇔B{\displaystyle A\Leftrightarrow B} означає «A{\displaystyle A} істинне тоді і тільки тоді, коли B{\displaystyle B} істинне». | x+5=y+2⇔x+3=y{\displaystyle x+5=y+2\Leftrightarrow x+3=y\,} |
| «тоді і тільки тоді» або «рівносильно» | ||||
| скрізь | ||||
| ∧{\displaystyle \wedge } | ∧ | Кон’юнкція | A∧B{\displaystyle A\wedge B} істинне тоді і тільки тоді, коли A{\displaystyle A} і B{\displaystyle B} обидва істині. | (n>2)∧(n<4)⇔(n=3){\displaystyle (n>2)\wedge (n<4)\Leftrightarrow (n=3)}, якщо n{\displaystyle n} — натуральне число. |
| «і» | ||||
| Математична логіка | ||||
| ∨{\displaystyle \vee } | ∨ | Диз’юнкція | A∨B{\displaystyle A\vee B} істинне, коли хоча б одна з умов A{\displaystyle A} або B{\displaystyle B} є істинною. | (n⩽2)∨(n⩾4)⇔n≠3{\displaystyle (n\leqslant 2)\vee (n\geqslant 4)\Leftrightarrow n\neq 3}, якщо n{\displaystyle n} — натуральне число. |
| «або» | ||||
| Математична логіка | ||||
| ¬{\displaystyle \neg } | ¬ | Заперечення | ¬A{\displaystyle \neg A} істинне тоді і тільки тоді, коли хибно A{\displaystyle A}. | ¬(A∧B)⇔(¬A)∨(¬B){\displaystyle \neg (A\wedge B)\Leftrightarrow (\neg A)\vee (\neg B)} x∉S⇔¬(x∈S){\displaystyle x\notin S\Leftrightarrow \neg (x\in S)} |
| «не» | ||||
| Математична логіка | ||||
| ∀{\displaystyle \forall } | ∀ | Квантор загальності | ∀x,P(x){\displaystyle \forall x,P(x)} означає «P(x){\displaystyle P(x)} істинне для всіх x{\displaystyle x}». | ∀n∈N,n2⩾n{\displaystyle \forall n\in \mathbb {N} ,\;n^{2}\geqslant n} |
| «Для будь-яких», «Для всіх» | ||||
| Математична логіка | ||||
| ∃{\displaystyle \exists } | ∃ | Квантор існування | ∃x,P(x){\displaystyle \exists x,\;P(x)} означає «існує хоча б одне x{\displaystyle x} таке, що P(x){\displaystyle P(x)} істинне» | ∃n∈N,n+5=2n{\displaystyle \exists n\in \mathbb {N} ,\;n+5=2n} (підходить число 5) |
| «існує» | ||||
| Математична логіка | ||||
| ={\displaystyle =\,} | = | Рівність | x=y{\displaystyle x=y} означає «x{\displaystyle x} і y{\displaystyle y} означають один і той же об’єкт». | 1 + 2 = 6 − 3 |
| «дорівнює» | ||||
| скрізь | ||||
| :={\displaystyle :=} :⇔{\displaystyle :\Leftrightarrow } =def{\displaystyle {\stackrel {\rm {def}}{=}}} | := :⇔ | Визначення | x:=y{\displaystyle x:=y} означає «x{\displaystyle x} за визначенням дорівнює y{\displaystyle y}». P:⇔Q{\displaystyle P:\Leftrightarrow Q} означає «P{\displaystyle P} за визначенням рівносильно Q{\displaystyle Q}» | ch(x):=12(ex+e−x){\displaystyle {\rm {ch}}(x):={1 \over 2}\left(e^{x}+e^{-x}\right)} (Гіперболічний косинус) A⊕B:⇔(A∨B)∧¬(A∧B){\displaystyle A\oplus B:\Leftrightarrow (A\vee B)\wedge \neg (A\wedge B)} (Виключаюче або) |
| «дорівнює/рівносильно за визначенням» | ||||
| скрізь | ||||
| {,}{\displaystyle \{,\}} | { , } | Множина елементів | {a,b,c}{\displaystyle \{a,\;b,\;c\}} означає множина, елементами якої є a{\displaystyle a}, b{\displaystyle b} та c{\displaystyle c}. | N={0,1,2,…}{\displaystyle \mathbb {N} =\{0,\;1,\;2,\;\ldots \}} (множина натуральних чисел) |
| «Множина…» | ||||
| Теорія множин | ||||
| {|}{\displaystyle \{|\}} {:}{\displaystyle \{:\}} | { | } { : } | Множина елементів, що задовольняють умові | {x|P(x)}{\displaystyle \{x\,|\,P(x)\}} означає множину усіх x{\displaystyle x} таких, що істинне P(x){\displaystyle P(x)}. | {n∈N|n2<20}={1,2,3,4}{\displaystyle \{n\in \mathbb {N} \,|\,n^{2}<20\}=\{1,\;2,\;3,\;4\}} |
| «Множина всіх… таких, що істинне…» | ||||
| Теорія множин | ||||
| ∅{\displaystyle \varnothing } {}{\displaystyle \{\}} | ∅ {} | Порожня множина | {}{\displaystyle \{\}} і ∅{\displaystyle \varnothing } означає множину, що не містить жодного елементу. | {n∈N|1<n2<4}=∅{\displaystyle \{n\in \mathbb {N} \,|\,1<n^{2}<4\}=\varnothing } |
| «Порожня множина» | ||||
| Теорія множин | ||||
| ∈{\displaystyle \in } ∉{\displaystyle \notin } | ∈ ∉ | приналежність/неприналежність до множини | a∈S{\displaystyle a\in S} означає «a{\displaystyle a} є елементом множини S{\displaystyle S}» a∉S{\displaystyle a\notin S} означає «a{\displaystyle a} не є елементом S{\displaystyle S}» | 2∈N{\displaystyle 2\in \mathbb {N} } 12∉N{\displaystyle {1 \over 2}\notin \mathbb {N} } |
| «належить», «з» «не належить» | ||||
| Теорія множин | ||||
| ⊆{\displaystyle \subseteq } ⊂{\displaystyle \subset } | ⊆ ⊂ | Підмножина | A⊆B{\displaystyle A\subseteq B} означає «кожний елемент з A{\displaystyle A} також є елементом з B{\displaystyle B}». A⊂B{\displaystyle A\subset B} як правило означає те ж, що і A⊆B{\displaystyle A\subseteq B}. Однак деякі автори використовують ⊂{\displaystyle \subset }, щоб показати строге включення (а саме ⊊{\displaystyle \subsetneq }). | (A∩B)⊆A{\displaystyle (A\cap B)\subseteq A} Q⊆R{\displaystyle \mathbb {Q} \subseteq \mathbb {R} } |
| «є підмножиною», «включено в» | ||||
| Теорія множин | ||||
| ⊊{\displaystyle \subsetneq } | ⫋ | Власна підмножина | A⊊B{\displaystyle A\subsetneq B} означає A⊆B{\displaystyle A\subseteq B} і A≠B{\displaystyle A\neq B}. | N⊊Q{\displaystyle \mathbb {N} \subsetneq \mathbb {Q} } |
| «є власною підмножиною», «строго включається в» | ||||
| Теорія множин | ||||
| ∪{\displaystyle \cup } | ∪ | Об’єднання | A∪B{\displaystyle A\cup B} означає множину елементів, що належать A{\displaystyle A} або B{\displaystyle B} (або обом одразу). | A⊆B⇔A∪B=B{\displaystyle A\subseteq B\Leftrightarrow A\cup B=B} |
| «Об’єднання … і …», «…, об’єднане з …» | ||||
| Теорія множин | ||||
| ∩{\displaystyle \cap } | ⋂ | Перетин | A∩B{\displaystyle A\cap B} означає множину елементів, що належать і A{\displaystyle A}, і B{\displaystyle B}. | {x∈R|x2=1}∩N={1}{\displaystyle \{x\in \mathbb {R} \,|\,x^{2}=1\}\cap \mathbb {N} =\{1\}} |
| «Перетин … і … », «…, перетнуте з …» | ||||
| Теорія множин | ||||
| ∖{\displaystyle \setminus } | \ | Різниця множин | A∖B{\displaystyle A\setminus B} означає множину елементів, що належать A{\displaystyle A}, але не належать B{\displaystyle B}. | {1,2,3,4}∖{3,4,5,6}={1,2}{\displaystyle \{1,\;2,\;3,\;4\}\setminus \{3,\;4,\;5,\;6\}=\{1,\;2\}} |
| «різниця … і … », «мінус», «… без …» | ||||
| Теорія множин | ||||
| →{\displaystyle \to } | → | Функція | f:X→Y{\displaystyle f\!\!:X\to Y} означає функцію f{\displaystyle f}, що відображає множину (область визначення) X{\displaystyle X} у множину Y{\displaystyle Y}. | Функція f:Z→Z{\displaystyle f\!\!:\mathbb {Z} \to \mathbb {Z} }, що визначення як f(x)=x2{\displaystyle f(x)=x^{2}} |
| «з … в», | ||||
| скрізь | ||||
| ↦{\displaystyle \mapsto } | ↦ | Відображення | x↦f(x){\displaystyle x\mapsto f(x)} означає, що образом x{\displaystyle x} після застосування функції f{\displaystyle f} буде f(x){\displaystyle f(x)}. | Функцію, що визначення як f(x)=x2{\displaystyle f(x)=x^{2}}, можна записати так: f:x↦x2{\displaystyle f\colon x\mapsto x^{2}} |
| «відображується в» | ||||
| скрізь | ||||
| N{\displaystyle \mathbb {N} } | N або ℕ | Натуральні числа | N{\displaystyle \mathbb {N} } означає множину {1,2,3,…}{\displaystyle \{1,\;2,\;3,\;\ldots \}} або {0,1,2,3,…}{\displaystyle \{0,\;1,\;2,\;3,\;\ldots \}} (в залежності від ситуації). | {|a||a∈Z}=N{\displaystyle \{\left|a\right|\,|\,a\in \mathbb {Z} \}=\mathbb {N} } |
| «Ен» | ||||
| Числа | ||||
| Z{\displaystyle \mathbb {Z} } | Z або ℤ | Цілі числа | Z{\displaystyle \mathbb {Z} } означає множину {…,−3,−2,−1,0,1,2,3,…}{\displaystyle \{\ldots ,\;-3,\;-2,\;-1,\;0,\;1,\;2,\;3,\;\ldots \}} | {a,−a|a∈N}=Z{\displaystyle \{a,\;-a\,|\,a\in \mathbb {N} \}=\mathbb {Z} } |
| «Зет» | ||||
| Числа | ||||
| Q{\displaystyle \mathbb {Q} } | Q або ℚ | Раціональні числа | Q{\displaystyle \mathbb {Q} } означає {pq|p∈Z∧q∈Z∧q≠0}{\displaystyle \left\{\left.{p \over q}\right|p\in \mathbb {Z} \wedge q\in \mathbb {Z} \wedge q\neq 0\right\}} | 3,14∈Q{\displaystyle 3,\!14\in \mathbb {Q} } π∉Q{\displaystyle \pi \notin \mathbb {Q} } |
| «Ку» | ||||
| Числа | ||||
| R{\displaystyle \mathbb {R} } | R або ℝ | Реальні числа, або дійсні числа | R{\displaystyle \mathbb {R} } означає множину всіх меж |
Символ | Название | Объяснение | Примеры | Значение Unicode | Название в HTML | Символ LaTeX |
|---|---|---|---|---|---|---|
| Читается как | ||||||
| Категория | ||||||
| Импликация | A ⇒ B верно, только когда либо A ложно, либо B истинно. → может означать то же самое, что и ⇒ (символ может также указывать область определения и область значений функции, см. таблицу математических символов). ⊃ может означать то же самое, что и ⇒ (символ может также обозначать надмножество). | x = 2 ⇒ x2 = 4 истинно, но x2 = 4 ⇒ x = 2, в общем случае, ложно (поскольку x может быть равен −2). | U+21D2 U+2192 U+2283 | ⇒ → ⊃ | ⇒{\displaystyle \Rightarrow }\Rightarrow →{\displaystyle \to }\to ⊃{\displaystyle \supset }\supset ⟹{\displaystyle \implies }\implies | |
| из .. следует; если .. то | ||||||
| логика высказываний, алгебра Гейтинга[en] | ||||||
| Тогда и только тогда | A ⇔ B истинно, только если оба значения A и B ложны, либо оба истинны. | x + 5 = y + 2 ⇔ x + 3 = y | U+21D4 U+2261 U+2194 | ⇔ ≡ ↔ | ⇔{\displaystyle \Leftrightarrow }\Leftrightarrow ≡{\displaystyle \equiv }\equiv ↔{\displaystyle \leftrightarrow }\leftrightarrow ⟺{\displaystyle \iff }\iff | |
| тогда и только тогда | ||||||
| логика высказываний | ||||||
| отрицание | Утверждение ¬A истинно тогда и только тогда, когда A ложно. Знак /, расположенный поверх другого оператора, означает то же самое, что «¬», помещённое перед выражением. | ¬(¬A) ⇔ A x ≠ y ⇔ ¬(x = y) | U+00AC U+02DC | ¬ ˜ ~ | ¬{\displaystyle \neg }\lnot или \neg ∼{\displaystyle \sim }\sim | |
| not (не) | ||||||
| логика высказываний | ||||||
| конъюнкция | Утверждение A ∧ B истинно, если и A, и B истинны, и ложно в противном случае. | n < 4 ∧ n >2 ⇔ n = 3, если n — натуральное число. | U+2227 U+0026 | ∧ & | ∧{\displaystyle \wedge }\wedge или \land \&[2] | |
| and (и) | ||||||
| логика высказываний, Булева алгебра | ||||||
| логическая дизъюнкция | Утверждение A ∨ B верно, если A или B (или оба) верны. Если оба не верны, утверждение неверно. | n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 когда n является натуральным числом. | U+2228 | ∨ | ∨{\displaystyle \lor }\lor или \vee | |
| or (или) | ||||||
| логика высказываний, Булева алгебра | ||||||
| исключающее или | Утверждение A ⊕ B верно, когда либо A, либо B верно, но не оба. A ⊻ B означает то же самое. | (¬A) ⊕ A всегда верно, A ⊕ A всегда неверно. | U+2295 U+22BB | ⊕ | ⊕{\displaystyle \oplus }\oplus ⊻{\displaystyle \veebar }\veebar | |
| xor | ||||||
| логика высказываний, Булева алгебра | ||||||
| Тавтология | Утверждение ⊤ безусловно верно. | A ⇒ ⊤ всегда верно. | U+22A4 | T | ⊤{\displaystyle \top }\top | |
| верх | ||||||
| логика высказываний, Булева алгебра | ||||||
| Противоречие | Утверждение ⊥ безусловно неверно. | ⊥ ⇒ A всегда верно. | U+22A5 | ⊥ F | ⊥{\displaystyle \bot }\bot | |
| ложь, неверно, ошибочно | ||||||
| логика высказываний, Булева алгебра | ||||||
| Квантор всеобщности | ∀ x: P(x) или (x) P(x) означает P(x) верно для всех x. | ∀ n ∈ ℕ: n2 ≥ n. | U+2200 | ∀ | ∀{\displaystyle \forall }\forall | |
| для любого; для всех | ||||||
| Логика первого порядка | ||||||
∃ | Квантор существования | ∃ x: P(x) означает, что существует по меньшей мере один x, такой, что P(x) верно. | ∃ n ∈ ℕ: n чётно. | U+2203 | ∃ | ∃{\displaystyle \exists }\exists |
| существует | ||||||
| логика первого порядка | ||||||
∃! | Единственность | ∃! x: P(x) означает, что существует ровно один x, такой, что P(x) верно. | ∃! n ∈ ℕ: n + 5 = 2n. | U+2203 U+0021 | ∃ ! | ∃!{\displaystyle \exists !}\exists ! |
| существует в точности один | ||||||
| логика первого порядка | ||||||
| Определение | x := y илиx ≡ y означает, что x является другим обозначением для y (но заметьте, что ≡ может означать и другое, как, например, конгруэнтность). P :⇔ Q означает, что P логически эквивалентно Q. | cosh x := (1/2)(exp x + exp (−x)) A XOR B :⇔ (A ∨ B) ∧ ¬(A ∧ B) | U+2254 (U+003A U+003D) U+2261 U+003A U+229C | := : ≡ ⇔ | :={\displaystyle :=}:= ≡{\displaystyle \equiv }\equiv ⇔{\displaystyle \Leftrightarrow }\Leftrightarrow | |
| определяется как | ||||||
| везде | ||||||
() | приоритетная группировка | Операции внутри скобок выполняются первыми. | (8 ÷ 4) ÷ 2 = 2 ÷ 2 = 1, но 8 ÷ (4 ÷ 2) = 8 ÷ 2 = 4. | U+0028 U+0029 | () | ( ){\displaystyle (~)} () |
| скобки | ||||||
| везде | ||||||
⊢ | Выводимо[en] | x ⊢ y означает, что y выводимо из x (в некоторых формальных системах). | A → B ⊢ ¬B → ¬A | U+22A2 | ⊢ | ⊢{\displaystyle \vdash }\vdash |
| выводимо | ||||||
| логика высказываний, логика первого порядка | ||||||
⊨ | Модель[en] | x ⊨ y означает, что x семантически влечёт за собой y | A → B ⊨ ¬B → ¬A | U+22A8 | ⊨ | ⊨{\displaystyle \vDash }\vDash |
| влечёт | ||||||
| логика высказываний, логика первого порядка |
