Отношения объектов — урок. Информатика, 6 класс.

Человек может рассказать не только о свойствах объекта, но и об отношениях, в которых этот объект находится с другими объектами.

Пример:

«Иван — сын Андрея»;
«Эверест выше Эльбруса»;
«Винни Пух дружит с Пятачком»;
«\(21\) кратно \(3\)»;
«Кострома такой же старинный город, как и Москва»;
«Текстовый процессор входит в состав программного обеспечения компьютера».

В каждом из приведённых предложений выделено имя отношения, которое обозначает характер связи между двумя объектами.

Отношения могут существовать не только между двумя объектами, но и между объектом и множеством объектов.

Пример:

«Дискета является носителем информации»;
«Камчатка — это полуостров (является полуостровом)».

В каждом из этих предложений описано отношение «является элементом множества».

Отношение может связывать два множества объектов.

Пример:

«Колёса входят в состав автомобилей»;
«Бабочки — это насекомые (являются разновидностью насекомых)».

Попарно связаны одним и тем же отношением могут быть несколько объектов. Соответствующее словесное описание может оказаться очень длинным, и тогда в нем трудно разобраться.

 

Пусть про населенные пункты А, Б, В, Г, Д и Е известно, что некоторые из них соединены железной дорогой:

населённый пункт А соединен железной дорогой с населёнными пунктами В, Г и Е,

населённый пункт Е — с населёнными пунктами В, Г и Д.

 

Для большей наглядности имеющиеся связи («соединён железной дорогой») можно изобразить линиями на схеме отношений. Объекты на схеме отношений могут быть изображены кругами, овалами, точками, прямоугольниками и т. д.

 

 

Имена некоторых отношений изменяются, когда меняются местами имена объектов, например: «выше» — «ниже», «приходится отцом» — «приходится сыном». В этом случае направление отношения обозначают стрелкой на схеме отношений.

Стрелки можно не использовать, если удаётся сформулировать и соблюсти правило взаимного расположения объектов на схеме.

 

 

Такие отношения, как «приходится сыном», «соединен железной дорогой», «покупает», «лечит» и т. д., могут связывать только объекты некоторых видов. А в отношениях «входит в состав» и «является разновидностью» могут находиться любые объекты.

Коротко о главном

В сообщении об объекте могут быть приведены не только свойства данного объекта, но и отношения, которые связывают его с другими объектами. Имя отношения обозначает характер этой связи. Отношения могут связывать не только два объекта, но и объект с множеством объектов или два множества.

 

Любые отношения между объектами можно наглядно описать с помощью схемы отношений. Объекты на схеме отношений могут быть изображены кругами, овалами, точками, прямоугольниками и т. д. Связи между объектами могут быть изображены линиями или стрелками.

Источники:

Босова Л. Л., Информатика и ИКТ : учебник для 7 класса. М. : БИНОМ. Лаборатория знаний, 15 с.

Отношение «входит в состав»

Вопросы занятия:

·                   объект как единое целое;

·                   объект как совокупность более мелких объектов;

·                   объект как некоторое количество подобных или различных объектов.

·                   схема отношений «входит в состав»;

Объект можно рассматривать не только как единое целое, а также как совокупность более мелких объектов.

Например, объект «парк». Для подсчёта количества парков в городе, будет браться целый объект. Для получения представление об одном конкретном парке, необходимо рассмотреть из чего он состоит.

В состав объекта могут входить как одинаковые элементы, так и множество различных. Примером одинаковых элементов, входящих в состав объекта, является мозаика, которая состоит из похожих частей – пазлов. Объект «парк» наоборот состоит из различных элементов: деревья (различных видов), цветы, скамейки и т.д. При рассмотрении данного объекта, его визуально делят на новые элементы (объекты).

Из примера вывод: с одной стороны, для описания состава объектов речь идёт о составе конкретного объекта, с другой стороны – об общих составных частях множества объектов. В последнем случае описание состава содержит ответ на вопрос: Из чего обычно состоят объекты некоторого множества?

Таким образом, чтобы описать парк, необходимо ответить на вопрос и выделить его составляющие: деревья (различных видов), цветы, дорожки, скамейки и т.д.

Для описания состава объекта, человеку необходимо мысленно разобрать его на части. При этом в первую очередь в объекте необходимо выделить большие части, а затем большие разбить на меньшие элементы и т.д.

Разберёмся на примере. Ученик Антон после уроков решил прогуляться по одному из парков города. После прогулки Антон решил написать электронное письмо своему однокласснику и описать всю красоту парка.

Для этого он изначально перечислил основные (более крупные) составляющие парка. Такие как деревья, цветы, лавочки, дорожки. Но понял, что этого слишком мало, чтобы описать всю красоту, поэтому он решил более подробно рассказать, что входит в каждое множество. Например, деревья он разделил на дубы и клёны. Цветы на тюльпаны, ромашки и нарциссы. Продолжая дальше описывать все объекты, которые он там увидел, Антон заметил, что все это можно представить в виде схемы. Вспомнив свой урок информатики, он понял, что эта схема будет называться «входит в состав» (схема состава объекта парк). Таким образом, начиная с самых больших объектов, разделяя их на более мелкие, он получил необходимую схему. При чём используя линии без стрелок, т.к. объект, который он разделял на части он располагал выше, чем саму часть объекта. В результате, кроме словесного описания, у него получилась следующая схема, предоставленная на рисунке. Исходя из этой схемы, Антон понял, что схема отношений «входит в состав» (схема состава) отображает элементы, из которых состоит объект, а также порядок, в котором объект разделялся на части. В схеме состава используются линии без стрелок, только в том случае, если имя объекта-части находится ниже имени объекта, которому принадлежит эта часть.

Таким образом, на схеме можно увидеть строение (структуру) объекта. Рассмотри подробно схему, которую получил Антон:

На данной схеме мы видим, что ученик для начала разделил парк на более крупные объекты: деревья, лавочки, дорожки и цветы. Затем некоторые объекты делятся на объекты-части. Таким образом, деревья были разделены на дубы и клёны. Т.е. объект «деревья» включает в себя объекты-части: дуб и клён. Таким же образом были разделены и цветы.

На данной схеме так же можно заметить множества «Деревья» и «Цветы», состоящие из элементов (других объектов), которые имеют своё имя и признаки. Т.к. имена объектов являются общими, то эта схема может подходить для описания не только того парка, в котором был Антон, но и для парков всего города.

Для описания признаков сложного, составного объекта человек может назвать не только действия и характеристики всего объекта, но также действия и свойства объектов частей. Например, деревья можно сажать, цветы поливать, лавочки красить, парк имеет площадь.

Важно запомнить!

·                   Объект можно рассматривать с двух различных сторон: 1. Как единое целое; 2. Как совокупность более мелких объектов.

·                   Объект может состоять из некоторого количества подобных или различных объектов.

·                   Схема отношений «входит в состав» отображает составные части объекта и порядок, в котором объект делился на части.

·                   В схеме состава используются линии без стрелок, только в том случае, если имя объекта-части находится ниже имени объекта, которому принадлежит эта часть.

Отношения между понятиями. Видеоурок. Информатика 6 Класс

Представляем вашему вниманию урок по теме «Отношения между понятиями». На нем вы сможете узнать, на основании каких признаков люди сравнивают реальные объекты. Также обсудите, что такое сравнимые и несравнимые понятия. В заключение рассмотрите, какие бывают отношения между понятиями.

На данном уроке будут рассмотрены следующие вопросы:

1. На основании каких признаков мы сравниваем реальные объекты?

2. Что такое сравнимые и несравнимые понятия?

3. Какие бывают отношения между понятиями?

Все понятия делятся на сравнимые и несравнимые.

Сравнимыми называют понятия, в содержании которых имеется хотя бы один общий признак. Почти все понятия являются сравнимыми.

Несравнимыми называют понятия, в содержании которых нет ни одного общего признака.

Сравнимые понятия делятся на совместимые (имеющие общие признаки)и несовместимые (не имеющие общих признаков). Сравнение происходит по содержанию и по объему.

Делятся на:

· Равнозначность;

· Пересечение;

· Подчинение.

Отношения между понятиями удобно представлять кругами. Такое представление называется диаграммами Эйлера – Венна (рис. 1).

Рис. 1. Диаграмма Эйлера – Венна

Равнозначными называют понятия, которые обозначают один и тот же объект.

Например: столица России обозначается кругом, город Москва обозначается точно таким же кругом. Столица России есть город Москва (рис. 2).

Рис. 2. Москва – столица России

Объекты, равно принадлежащие и к одному, и к другому множеству объектов.

Например: если пересечь множество всех горнолыжников с множеством всех детей, то мы получим множество детей-горнолыжников (рис. 3).

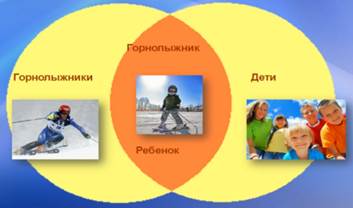
Рис. 3. Множество детей-горнолыжников

Отношения между понятиями, когда объем одного из них входит в объем другого понятия, но не исчерпывает его.

Родовые и видовые понятия всегда относятся в отношении подчинения.

Например: в род насекомых входят различные виды (пауки, бабочки и т. д.) (рис. 4).

Рис. 4. Отношения подчинения

Делятся на:

· Соподчинение;

· Противоположность;

· Противоречие.

Несовместимые понятия – понятия, объемы которых не имеют общих объектов.

Например: банан и компьютер (рис. 5).

Рис. 5. Несовместимые понятия

Это отношение между понятиями, объемы которых не пересекаются (исключительно друг с другом), но принадлежат общему (родовому) понятию.

Например: клены, березы и ели являются деревьями, но между собой эти понятия не пересекаются (рис. 6).

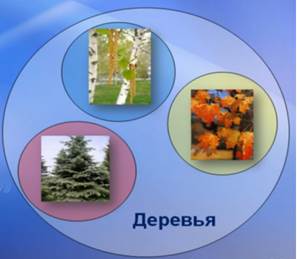
Рис. 6. Отношение соподчинения

Слова, выражающие противоположные понятия, называются антонимами (рис. 7). Отношения противоположности выражаются тем, что нет общих пересечений.

Например: истина – ложь, черный – белый, храбрость – трусость.

Рис. 7. Антонимы

Понятие, находящееся в противоречии с понятием А, обозначают не-А.

Понятия А и не-А (рис. 8) являются антонимами.

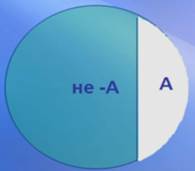
Рис. 8. Отношения противоречия

Например: черный – не-черный, белый – не-белый, умный – не-умный.

 

Список литературы

1. Босова Л.Л. Информатика и ИКТ: учебник для 6 класса. – М.: БИНОМ. Лаборатория знаний, 2012.

2. Босова Л.Л. Информатика: рабочая тетрадь для 6 класса. – М.: БИНОМ. Лаборатория знаний, 2010.

3. Босова Л.Л., Босова А.Ю. Уроки информатики в 5–6 классах: методическое пособие. – М.: БИНОМ. Лаборатория знаний, 2010.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

 

1. Интернет портал «Фестиваль педагогических идей» (Источник)

2. Интернет портал «lib.podelise.ru/» (Источник)

 

Домашнее задание

1. §2.3 (Босова Л.Л. Информатика и ИКТ: учебник для 6 класса).

2. Стр. 53 задание 1–9 (Босова Л.Л. Информатика и ИКТ: учебник для 6 класса).

Онтология (информатика) — Википедия

Онтоло́гия в информатике (новолат. ontologia от др.-греч. ὤν род. п. ὄντος — сущее, то, что существует и λόγος — учение, наука) — это попытка всеобъемлющей и подробной формализации некоторой области знаний с помощью концептуальной схемы. Обычно такая схема состоит из структуры данных, содержащей все релевантные классы объектов, их связи и правила (теоремы, ограничения), принятые в этой области. Этот термин в информатике является производным от древнего философского понятия «онтология».

Онтологии используются в процессе программирования как форма представления знаний о реальном мире или его части. Основные сферы применения — моделирование бизнес-процессов, семантическая паутина (англ. Semantic Web), искусственный интеллект.

Отличия от философского понятия онтологии[править | править код]

Хотя термин «онтология» изначально философский, в информатике он принял самостоятельное значение. Здесь есть два существенных отличия:

• Онтология в информатике должна иметь формат, который компьютер сможет легко обработать;
• Информационные онтологии создаются всегда с конкретными целями — решения конструкторских задач; они оцениваются больше с точки зрения применимости, чем полноты.

Современные онтологии строятся по большей части одинаково, независимо от языка написания. Обычно они состоят из экземпляров, понятий, атрибутов и отношений.

Экземпляры[править | править код]

Экземпляры (англ. instances) или индивиды (англ. individuals) — это объекты, основные нижнеуровневые компоненты онтологии; могут представлять собой как физические объекты (люди, дома, планеты), так и абстрактные (числа, слова). Строго говоря, онтология может обойтись и без конкретных объектов, однако, одной из главных целей онтологии является классификация таких объектов, поэтому они также включаются.

Понятия[править | править код]

Понятия (англ. concepts) или классы (англ. classes) — абстрактные группы, коллекции или наборы объектов. Они могут включать в себя экземпляры, другие классы либо же сочетания и того, и другого. Пример:

• Понятие «люди», вложенное понятие «человек». Чем является «человек» — вложенным понятием, или экземпляром (индивидом) — зависит от онтологии.
• Понятие «индивиды», экземпляр «индивид».

Классы онтологии составляют таксономию — иерархию понятий по отношению вложения^[1].

Атрибуты[править | править код]

Объекты в онтологии могут иметь атрибуты. Каждый атрибут имеет по крайней мере имя и значение и используется для хранения информации, которая специфична для объекта и привязана к нему. Например, объект Автомобиль-модели-А имеет такие атрибуты, как:

• Название: Автомобиль-модели-А
• Число-дверей: 4
• Двигатель: {4.0Л, 4.6Л}
• Коробка-передач: 6-ступенчатая

Значение атрибута может быть сложным типом данных. В данном примере значение атрибута, который называется Двигатель, является списком значений простых типов данных.

Отношения[править | править код]

Важная роль атрибутов заключается в том, чтобы определять отношения (зависимости) между объектами онтологии. Обычно отношением является атрибут, значением которого является другой объект.

Предположим, что в онтологии автомобилей присутствует два объекта — автомобиль Автомобиль-модели-А и Автомобиль-модели-Б. Пусть Автомобиль-модели-Б это модель-наследник Автомобиль-модели-А, тогда отношение между Автомобиль-модели-А и Автомобиль-модели-Б определим как атрибут «isSuccessorOf» со значением «Автомобиль-модели-А» для объекта Автомобиль-модели-Б (следует заметить, что в языках описания онтологий существуют предопределенные отношения наследования).

Специализированные и общие онтологии[править | править код]

Специализированные (предметно-ориентированные) онтологии — это представление какой-либо области знаний или части реального мира. В такой онтологии содержатся специальные для этой области значения терминов. К примеру, слово «поле» в сельском хозяйстве означает участок земли, в физике — один из видов материи, в математике — класс алгебраических систем.

Общие онтологии используются для представления понятий, общих для большого числа областей. Такие онтологии содержат базовый набор терминов, глоссарий или тезаурус, используемый для описания терминов предметных областей.

Если использующая специализированные онтологии система развивается, то может потребоваться их объединение. Подзадачей объединения онтологий является задача отображения онтологий. И для инженера по онтологиям это серьёзная задача. Онтологии даже близких областей могут быть несовместимы друг с другом. Разница может появляться из-за особенностей местной культуры, идеологии или вследствие использования другого языка описания. Объединение онтологий выполняют как вручную, так и в полуавтоматическом режиме. В целом это — трудоёмкий, медленный и дорогостоящий процесс. Использование базисной онтологии — единого глоссария — несколько упрощает эту работу. Есть научные работы по технологиям объединения, но они по большей части теоретические.

Язык описания онтологий — формальный язык, используемый для кодирования онтологии. Существует несколько подобных языков (список неполон):

Для работы с языками онтологий существует несколько видов технологий: редакторы онтологий (для создания онтологий), СУБД онтологий (для хранения и обращения к онтологии) и хранилища онтологий (для работы с несколькими онтологиями).

Информационные отношения — это… Что такое Информационные отношения?



Информационные отношения

«…Информационные отношения — отношения, возникающие при обработке, сборе, хранении, распространении и использовании информации…»

Источник:

Решение Совета глав государств СНГ

«О Концепции сотрудничества государств-участников Содружества Независимых Государств в сфере обеспечения информационной безопасности и о Комплексном плане мероприятий по реализации Концепции сотрудничества государств-участников Содружества Независимых Государств в сфере обеспечения информационной безопасности на период с 2008 по 2010 год»

Официальная терминология. Академик.ру. 2012.

• Информационные надписи на транспортном средстве
• Информационные программы

Смотреть что такое «Информационные отношения» в других словарях:

• ОТНОШЕНИЯ ОБЩЕСТВЕННЫЕ —     ОТНОШЕНИЯ ОБЩЕСТВЕННЫЕ отношения, включающие в качестве своих элементов: 1) субъектов с их статусами и ролями, ценностями и нормами, потребностями и интересами, стимулами и мотивами; 2) содержание деятельности субъектов и их взаимодействий,… …   Философская энциклопедия

• Информационные технологии управления муниципальной недвижимостью — Основы функционирование рынка Необходимое условие функционирования рынка недвижимости наличие информационной инфраструктуры, обеспечивающей субъекты рынка актуальной, полной и достоверной информацией о следующих аспектах рыночной системы:… …   Википедия

• Информационные процессы — Информационный процесс процесс получения, создания, сбора, обработки, накопления, хранения, поиска, распространения и использования информации.[1] В результате исполнения информационных процессов осуществляются информационные права и свободы,… …   Википедия

• ИНФОРМАЦИОННЫЕ РЕСУРСЫ — отдельные документы и отдельные массивы документов, документы и массивы документов в информационных системах (библиотеках, архивах, фондах, банках данных, других информационных системах). И.р. являются объектом права собственности. И.р. могут… …   Энциклопедический словарь экономики и права

• Общественные отношения — отношения между людьми, живущими достаточно большими группами, складывающиеся в процессе развития общества. На различных этапах развития общества ведущую роль играют те или иные общественные отношения: религиозные, кастовые, производственные,… …   Теоретические аспекты и основы экологической проблемы: толкователь слов и идеоматических выражений

• ГОСТ Р 52438-2005: Географические информационные системы. Термины и определения — Терминология ГОСТ Р 52438 2005: Географические информационные системы. Термины и определения оригинал документа: 57 (топологический) оверлей: Наложение двух или более полигональных объектов, в результате которого образуется новый слой, состоящий… …   Словарь-справочник терминов нормативно-технической документации

• 50.1.031-2001: Информационные технологии поддержки жизненного цикла продукции. Терминологический словарь. Часть 1. Стадии жизненного цикла продукции — Терминология 50.1.031 2001: Информационные технологии поддержки жизненного цикла продукции. Терминологический словарь. Часть 1. Стадии жизненного цикла продукции: 3.7.12. (всеобщее) управление качеством : Совокупность программных средств и данных …   Словарь-справочник терминов нормативно-технической документации

• Р 50.1.031-2001: Информационные технологии поддержки жизненного цикла продукции. Терминологический словарь. Часть 1. Стадии жизненного цикла продукции — Терминология Р 50.1.031 2001: Информационные технологии поддержки жизненного цикла продукции. Терминологический словарь. Часть 1. Стадии жизненного цикла продукции: 3.7.12. (всеобщее) управление качеством : Совокупность программных средств и… …   Словарь-справочник терминов нормативно-технической документации

• Международные экономические отношения — (МЭО)  экономические отношения между государствами, региональными группировками, транснациональными корпорациями и другими субъектами мирового хозяйства. Включают валютно финансовые, торговые, производственные, трудовые и другие отношения.… …   Википедия

• ГОСТ Р ИСО/МЭК 19762-1-2011: Информационные технологии. Технологии автоматической идентификации и сбора данных (АИСД). Гармонизированный словарь. Часть 1. Общие термины в области АИСД — Терминология ГОСТ Р ИСО/МЭК 19762 1 2011: Информационные технологии. Технологии автоматической идентификации и сбора данных (АИСД). Гармонизированный словарь. Часть 1. Общие термины в области АИСД оригинал документа: Accredited Standards… …   Словарь-справочник терминов нормативно-технической документации

Бинарное отношение — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 мая 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 мая 2019; проверки требует 1 правка. У этого термина существуют и другие значения, см. Отношение.

Бина́рное (двухместное) отноше́ние — отношение между двумя множествами A{\displaystyle A} и B{\displaystyle B}, то есть всякое подмножество декартова произведения этих множеств: R⊆A×B{\displaystyle R\subseteq A\times B}^[1]. Бинарное отношение на множестве A{\displaystyle A} — любое подмножество R⊆A2=A×A{\displaystyle R\subseteq A^{2}=A\times A}, такие бинарные отношения наиболее часто используются в математике, в частности, таковы равенство, неравенство, эквивалентность, отношение порядка.

• Множество всех первых компонент пар из R⊆A×B{\displaystyle R\subseteq A\times B} называется областью определения отношения R{\displaystyle R} и обозначается как DomR{\displaystyle \mathrm {Dom} \,R}.

DomR={x∣∃y((x,y)∈R)}.{\displaystyle \mathrm {Dom} \,R=\{x\mid \exists y((x,\;y)\in R)\}.}

• Множество всех вторых компонент пар из R{\displaystyle R} называется областью значения отношения R{\displaystyle R} и обозначается как ImR{\displaystyle \mathrm {Im} \,R}.

ImR={y∣∃x((x,y)∈R)}.{\displaystyle \mathrm {Im} \,R=\{y\mid \exists x((x,\;y)\in R)\}.}

Бинарное отношение R{\displaystyle R} на некотором множестве M{\displaystyle M} может обладать различными свойствами, например:

• рефлексивность: ∀x∈M:(xRx){\displaystyle \forall x\in M:(xRx)},
• антирефлексивность (иррефлексивность): ∀x∈M:¬(xRx){\displaystyle \forall x\in M:\neg (xRx)},
• корефлексивность: ∀x,y∈M:(xRy⇒x=y){\displaystyle \forall x,y\in M:(xRy\Rightarrow x=y)},
• симметричность: ∀x,y∈M:(xRy⇒yRx){\displaystyle \forall x,\;y\in M:(xRy\Rightarrow yRx)},
• антисимметричность: ∀x,y∈M:(xRy∧yRx⇒x=y){\displaystyle \forall x,\;y\in M:(xRy\wedge yRx\Rightarrow x=y)},
• асимметричность: ∀x,y∈M:(xRy⇒¬(yRx)){\displaystyle \forall x,\;y\in M:(xRy\Rightarrow \neg (yRx))},
• транзитивность: ∀x,y,z∈M:(xRy∧yRz⇒xRz){\displaystyle \forall x,\;y,\;z\in M:(xRy\wedge yRz\Rightarrow xRz)},
• евклидовость: ∀x,y,z∈M:(xRy∧xRz⇒yRz){\displaystyle \forall x,y,z\in M:(xRy\wedge xRz\Rightarrow yRz)},
• полнота (или связность^[2]): ∀x,y∈M:(xRy∨yRx){\displaystyle \forall x,y\in M:(xRy\lor yRx)},
• связность (или слабая связность^[2]): ∀x,y∈M:(x≠y⇒xRy∨yRx){\displaystyle \forall x,y\in M:(x\neq y\Rightarrow xRy\lor yRx)},
• коннексность (англ. connex): ∀x,y∈M:(xRy∨yRx∨x=y){\displaystyle \forall x,y\in M:(xRy\lor yRx\lor x=y)},
• трихотомия: ∀x,y∈M{\displaystyle \forall x,y\in M} верно ровно одно из трех утверждений: xRy{\displaystyle xRy}, yRx{\displaystyle yRx} или x=y{\displaystyle x=y}.

Виды бинарных отношений[править | править код]

• Обратное отношение^{[уточнить]} (отношение, обратное к R{\displaystyle R}) — это двухместное отношение, состоящее из пар элементов (y,x){\displaystyle (y,x)}, полученных перестановкой пар элементов (x,y){\displaystyle (x,y)} данного отношения R{\displaystyle R}. Обозначается: R−1{\displaystyle R^{-1}}. Для данного отношения и обратного ему верно равенство: (R−1)−1=R{\displaystyle (R^{-1})^{-1}=R}.
• Взаимо-обратные отношения (взаимообратные отношения) — отношения, являющиеся обратными друг по отношению к другу. Область значений одного из них служит областью определения другого, а область определения первого — областью значений другого.
• Рефлексивное отношение — двухместное отношение R{\displaystyle R}, определённое на некотором множестве и отличающееся тем, что для любого x{\displaystyle x} этого множества элемент x{\displaystyle x} находится в отношении R{\displaystyle R} к самому себе, то есть для любого элемента x{\displaystyle x} этого множества имеет место xRx{\displaystyle xRx}. Примеры рефлексивных отношений: равенство, одновременность, сходство.
• Антирефлексивное отношение (иррефлексивное отношение; так же, как антисимметричность не совпадает с несимметричностью, иррефлексивность не совпадает с нерефлексивностью) — бинарное отношение R{\displaystyle R}, определённое на некотором множестве и отличающееся тем, что для любого элемента x{\displaystyle x} этого множества неверно, что оно находится в отношении R{\displaystyle R} к самому себе (неверно, что xRx{\displaystyle xRx}).
• Транзитивное отношение — двухместное отношение R{\displaystyle R}, определённое на некотором множестве и отличающееся тем, что для любых x,y,z{\displaystyle x,y,z} из xRy{\displaystyle xRy} и yRz{\displaystyle yRz} следует xRz{\displaystyle xRz} (xRy∧yRz→xRz{\displaystyle xRy\wedge yRz\to xRz}). Примеры транзитивных отношений: «больше», «меньше», «равно», «подобно», «выше», «севернее».
• Нетранзитивное отношение^{[уточнить]} — двухместное отношение R{\displaystyle R}, определённое на некотором множестве и отличающееся тем, что для любых x,y,z{\displaystyle x,y,z} этого множества из xRy{\displaystyle xRy} и yRz{\displaystyle yRz} не следует xRz{\displaystyle xRz} (¬(xRy∧yRz→xRz){\displaystyle \neg (xRy\wedge yRz\to xRz)}). Пример нетранзитивного отношения: «x отец y»
• Симметричное отношение — бинарное отношение R{\displaystyle R}, определённое на некотором множестве и отличающееся тем, что для любых элементов x{\displaystyle x} и y{\displaystyle y} этого множества из того, что x{\displaystyle x} находится к y{\displaystyle y} в отношении R{\displaystyle R}, следует, что и y{\displaystyle y} находится в том же отношении к x{\displaystyle x} — xRy→yRx{\displaystyle xRy\to yRx}. Примером симметричных отношений могут быть равенство, отношение эквивалентности, подобие, одновременность.
• Антисимметричное отношение — бинарное отношение R{\displaystyle R}, определённое на некотором множестве и отличающееся тем, что для любых x{\displaystyle x} и y{\displaystyle y} из xRy{\displaystyle xRy} и yRx{\displaystyle yRx} следует x=y{\displaystyle x=y} (то есть R{\displaystyle R} и R−1{\displaystyle R^{-1}} выполняются одновременно лишь для равных между собой членов).
• Асимметричное отношение — бинарное отношение R{\displaystyle R}, определённое на некотором множестве и отличающееся тем, что для любых x{\displaystyle x} и y{\displaystyle y} из xRy{\displaystyle xRy} следует ¬yRx{\displaystyle \neg yRx}. Пример: отношения «больше» (>) и «меньше» (<).
• Отношение эквивалентности — бинарное отношение R{\displaystyle R} между объектами x{\displaystyle x} и y{\displaystyle y}, являющееся одновременно рефлексивным, симметричным и транзитивным. Примеры: равенство, равномощность двух множеств, подобие, одновременность.
• Отношение порядка — отношение, обладающие только некоторыми из трёх свойств отношения эквивалентности: отношение рефлексивное и транзитивное, но несимметричное (например, «не больше») образует нестрогий порядок, а отношение транзитивное, но нерефлексивное и несимметричное (например, «меньше») — строгий порядок.
• Функция одного переменного — бинарное отношение R{\displaystyle R}, определённое на некотором множестве, отличающееся тем, что каждому значению x{\displaystyle x} отношения xRy{\displaystyle xRy} соответствует лишь единственное значение y{\displaystyle y}. Свойство функциональности отношения R{\displaystyle R} записывается в виде аксиомы: (xRy∧xRz)→(y≡z){\displaystyle (xRy\wedge xRz)\to (y\equiv z)}.
• Биекция (взаимно-однозначное отношение) — бинарное отношение R{\displaystyle R}, определённое на некотором множестве, отличающееся тем, что в нём каждому значению x{\displaystyle x} соответствует единственное значение y{\displaystyle y}, и каждому значению y{\displaystyle y} соответствует единственное значение x{\displaystyle x}.
• Связанное отношение — бинарное отношение R{\displaystyle R}, определённое на некотором множестве, отличающееся тем, что для любых двух различных элементов x{\displaystyle x} и y{\displaystyle y} из этого множества, одно из них находится в отношении R{\displaystyle R} к другому (то есть выполнено одно из двух соотношений: xRy{\displaystyle xRy} или yRx{\displaystyle yRx}). Пример: отношение «меньше» (<).

Так как отношения, заданные на фиксированной паре множеств A{\displaystyle A} и B{\displaystyle B} суть подмножества множества A×B{\displaystyle A\times B}, то совокупность всех этих отношений образует булеву алгебру относительно операций объединения, пересечения и дополнения отношений. В частности, для произвольных a∈A{\displaystyle a\in A}, b∈B{\displaystyle b\in B}:

a(R∪S)b⇔aRb∨aSb{\displaystyle a\,(R\cup S)\,b\Leftrightarrow a\,R\,b\vee a\,S\,b},

a(R∩S)b⇔aRb∧aSb{\displaystyle a\,(R\cap S)\,b\Leftrightarrow a\,R\,b\wedge a\,S\,b},

aR¯b⇔¬aRb{\displaystyle a\,{\overline {R}}\,b\Leftrightarrow \neg a\,R\,b}.

Часто вместо объединения, пересечения и дополнения отношений говорят об их дизъюнкции, конъюнкции и отрицании.

Например, (=)∪(<)=(⩽){\displaystyle ({=})\cup ({<})=({\leqslant })}, (=)∩(<)=∅{\displaystyle ({=})\cap ({<})=\varnothing }, то есть объединение отношения строгого порядка с отношением равенства совпадает с отношением нестрогого порядка, а их пересечение пусто.

Кроме перечисленных важное значение имеют ещё операции обращения и умножения отношений, определяемые следующим образом. Если R⊆A×B{\displaystyle R\subseteq A\times B}, то обратным отношением называется отношение R−1{\displaystyle R^{-1}}, определённое на паре B{\displaystyle B}, A{\displaystyle A} и состоящее из тех пар (b,a){\displaystyle (b,a)}, для которых aRb{\displaystyle a\,R\,b}. Например, (<)−1=(>){\displaystyle ({<})^{-1}=({>})}.

Пусть R⊆A×B{\displaystyle R\subseteq A\times B}, S⊆B×C{\displaystyle S\subseteq B\times C}. Композицией (или произведением) отношений R{\displaystyle R} и S{\displaystyle S} называется отношение R∘S⊆A×C{\displaystyle R\circ S\subseteq A\times C} такое, что:

a(R∘S)c⇔∃b∈B:a(R)b∧b(S)c{\displaystyle a\,(R\circ S)\,c\Leftrightarrow \exists b\in B:\,a\,(R)\,b\wedge b\,(S)\,c}.

Например, для отношения строгого порядка на множестве натуральных числе его умножение на себя определено следующим образом: a(<)(<)b⇔a+1<b{\displaystyle a({<})({<})b\Leftrightarrow a+1<b}

Урок по информатике в 6 классе на тему «Отношения между понятиями»

Отношения между понятиями. Тождество. Пересечение. Подчинение.

Урок информатики в 6 классе

Учитель информатики филиала МОУ «СОШ» с Каменка в с Чернавка Шершнева Л.Н.

Тип урока: изучение новой темы

Вид урока: комбинированный

Цели:

• Учебная: сформировать у учащихся знания об общих подходах к сравнению понятий тождества, пересечения и подчинения;

• Развивающая: развитие у школьников теоретического, творческого мышления, а также формирование операционного мышления, направленного на выбор оптимальных решений с помощью заполнения карточки-конспекта, практической работы.

• Воспитательная: развитие умения слушать и слышать; развитие познавательного интереса; воспитание информационной культуры.

Знания и умения: отношение тождества, отношение пересечения, отношение подчинения, учащиеся должны научиться решать информационные задачи с помощью диаграмм, должны уметь рассуждать, должны уметь обосновывать свои действия, учатся систематизировать.

Используемые педагогические технологии: обучение с помощью ИКТ, игровые технологии, здоровьесберегающие технологии, элементы технологии проблемного обучения, элементы технологий развивающего обучения.

Технические средства обучения: ПК, мультимедиапроектор, Карточки с заданиями в ГР, мультимедийная презентация.

План урока.

1. Организационный момент (2 мин.)

2. Актуализация знаний (5 мин.)

3. Изучение новой темы (10 мин.)

4. Закрепление новой темы.(5 мин.)

Физкультминутка (1 мин.)

5. Работа за компьютерами (14 мин.)

Физкультминутка (упражнения для глаз)(1 мин.)

6. Подведение итогов урока, рефлексия (5 мин.)

7. Домашнее задание (2 мин.)

Ход урока.

I. Организационный момент.

Сообщение темы и цели урока.

Здравствуйте ребята! Тема сегодняшнего урока «Отношения между понятиями». Сегодня мы познакомимся с общими подходами к сравнению понятий; а так же узнаем что такое отношения тождества, пересечения, подчинения при сравнении понятий; продолжим развивать логическое мышление, познавательный интерес, аккуратность, внимательность и навыки работы на компьютере. Надеюсь, наша совместная работа будет дружеской и деловой.

Итак начнем.

II. Актуализация знаний.

Всех нас в реальной жизни окружает множество объектов.

Приведите примеры объектов, которые окружают нас с вами сейчас. Молодцы.

Как можно описать любой предмет? (Любой объект может быть описан с помощью каких-либо признаков). Т.е. любой объект может быть описан словами.

Понятия – это наши представления, наши мысли об объектах. При сравнении понятий сравнивают их содержания и их объемы.

В отличие от объектов реальной действительности, понятия не имеют ни цвета, ни запаха, ни размера.

Расширим наше представление о понятиях.

(слайды 3-10) Разбить понятия на пары, у которых есть общий признак и указать этот общий признак.

стол

стул

мебель

монитор

принтер

устройство вывода

гвоздь

пила

инструмент

весна

осень

время года

квадрат

прямоугольник

геометрические фигуры

радуга

——

——

самолет

(слайд 11) Понятия, имеющие общий признак, называются сравнимыми.

Понятия, не имеющие общих признаков, называются несравнимыми.

(слайд 12) Сравним содержания понятий квадрат и прямоугольник.

Понятие

Содержание

квадрат

• четырехугольник

• все углы прямые

• все стороны равны

прямоугольник

• четырехугольник

• все углы прямые

• длины противоположных сторон попарно равны

Сравним объемы этих понятий.

Объем понятия «прямоугольник» шире объема понятия «квадрат», так как все квадраты – тоже прямоугольники.

(слайд 13) Отношения между понятиями удобно представлять кругами, например:

где А – объем понятия «прямоугольник»

В – объем понятия «квадрат»

Такое представление называется кругами Эйлера.

Крупнейший ученый 18 в. Леонард Эйлер (1707–1783) (большую часть творческой жизни провел в Петербурге) предложил изображать понятия и отношения между ними круговыми схемами. С этого момента данные схемы повсеместно применяются в логике. Мы также используем их и при рассмотрении отношений между понятиями.

(слайд 14) Для закрепления полученных знаний выполним задание № 2 (рабочая тетрадь стр. 53 № 25)

– Молодцы! Дома доделайте это упражнение до конца.

III. Изучение новой темы

Рассмотрим отношения между понятиями по объему, обозначая объемы понятий кругами Эйлера-Венна.

(Слайд 15) Первое отношение между понятиями, которое вам необходимо запомнить называется отношением «тождество» — это отношение между понятиями, объемы которых совпадают, другими словами объем одного понятия равен объему другого.

Объемы тождественных понятий изображаются кругами, полностью совпадающими.

(слайд 16) Примеры равнозначных понятий:

1) «Волга» и «самая длинная река в Европе»;

2) «Великий русский царь» и «Создатель Российского флота».

3) «Москва» и «столица нашей Родины».

(слайд 17) Второе отношение в котором могут находиться понятия это отношение «пересечение».

Рассмотрим два понятия “Электронное письмо” и “письмо на русском языке”. Они изображаются пересекающимися кругами. Круг А электронное письмо, круг В Письмо на русском языке, а в пересечении «Электронное письмо на русском языке».

Отношение между понятиями, объемы которых совпадают частично, т.е. содержат общие элементы называется отношением пересечения.

А – Электронное письмо, В – Письмо на русском языке

А В

общие элементы (Электронное письмо на русском языке)

(слайд 18) Еще один пример сравним понятия «Ученики класса» и «Хорошисты школы»

(слайд 19) Следующий пример, рассмотрим понятия «Времена года» и «Зима». Что вы можете сказать об этих понятиях? То есть понятие «Зима» полностью входит в понятие «Времена года», но не исчерпывает его. Такое отношение называется «подчинением».

Отношение подчинения – это отношение между понятиями, когда объем одного понятия полностью входит в объем другого понятия, но не исчерпывает его.

( слайд 20) Примером понятий находящихся отношении подчинения являются:

А – животные, В – кошка.

IV. Закрепление новой темы

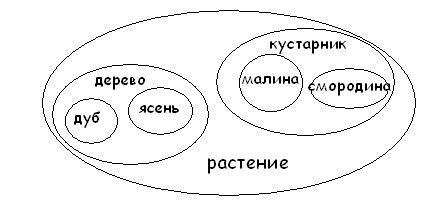
(слайд 21) Определить отношения между понятиями и изобразить эти отношения по образцу.

Понятия: дуб, растения, ясень, дерево, кустарник, малина, смородина.

(слайд 22) Физкультминутка

А теперь, ребята, встать,

Руки медленно поднять,

Пальцы сжать, потом разжать,

Руки вниз, и так стоять.

Наклонитесь вправо, влево

И беритесь вновь за дело

V. Компьютерный практикум. 

Техника безопасности

(слайд 23) На сегодняшней практической работе мы с вами будем работать в программе Paint. Работа №9, задание 4.

Выполнив задание сохраните его под именем Клоун в своей папке.

(слайд 24) Теперь поработаем с логическим диском.

Auyorun «Издательство Учитель»

Запуск

Множества

Взаимное расположение

Практика

Задания № 6,7,8,9,10

Выполнив задания, нажмите ок, проверьте результат.

Физкультминутка, упражнения для глаз.

Выставление оценок. 
Проверка работ. Оценки за урок:… 
VI. Домашнее задание:
параграф 2.3. стр. 45-48, Р.Т № 25, 27. 
VII. Итог урока. Рефлексия
Давайте подведем итогом. 
С какими отношениями между понятиями мы сегодня познакомились? (Тождество, пересечение, подчинение)

У вас на столе листочки с рисунками, на обратной стороне небольшая анкета, пожалуйста заполните ее. 
Молодцы ребята. Я желаю вам побольше хороших оценок и удачи всегда и во всем.   
Спасибо за урок! До свидания! 

Список использованной литературы и источников сети Интернет 
1. Босова Л.Л. Информатика: Учебник для 6 класса/Л.Л.Босова.-5-е изд.-М.БИНОМ. Лаборатория знаний, 2007.-208с.: ил. 
2. Уроки информатики в 5-6 классах: Методическое пособие/ Л.Л.Босова, А.Ю. Босова. – 2-у изд., испр. и доп.- М.: БИНОМ. Лаборатория знаний, 2008. – 320 с.: ил. 

3. http://www.school-collection.edu.ru
4. http://www.s8ach.narod.ru
5. http://www.festival.1september.ru