Шифт математика: Олимпиадная и развивающая математика

25.04.1972 alexxlab 0

Содержание

«SHIFT» – Городской лагерь в Санкт-Петербурге

Программа

Новогодняя Программа:
Новогодние праздники длинные, а занять ребенка нечем?

Тогда присоединяйтесь к зимней смене, где будут не только развлечения и отдых, но и образовательная начинка от нашей школы.
Мы подготовили специальные зимние интенсивы, а значит ваш ребенок прокачает свои навыки коммуникации и логическое мышление, а в конце представит собственный проект. Отдых и развитие в одном флаконе!

Лето — отличное время попробовать новое. Мы хотим поддержать это рвение у детей, поэтому в нашем лагере работают 3 мастерские:

  • Творческая: актерское мастерство, видео съемка и обработка, графический дизайн;
  • Языковая: английский язык;
  • Техническая: математика, программирование.
Также в программе лагеря:
  • Утренняя зарядка.
  • Прогулки.
  • Настольные игры.

Распорядок дня

  • 09:00 – 09:30 Сбор детей (Ждем опаздывающих, рассказываем, что нас ждет).
  • 09:30 – 09:45 Утренняя зарядка (Просыпаемся и готовимся к продуктивному дню).
  • 09:45 – 10:15 Легкий завтрак (Заряжаемся энергией для новых открытий).
  • 10:30 – 12:00 Студия (Занятие по выбранному направлению).
  • 12:15 – 13:30 Прогулка (Играем в Таврическом саду, при плохой погоде проводим время за интеллектуальными играми).
  • 13:40 – 14:20 Обед (Комплексный обед из 2 блюд + напиток).
  • 14:30 – 15:30 Время для мероприятия (Играем с в настольные игры, приглашаем экспертов в области программирования, VR/AR, блогинга).
  • 15:30 – 17:00 Мастерская (Занятие по выбранному направлению).
  • 17:10 – 17:30 Перекус (Никто не поедет домой голодным).
  • 17:30 – 18:00 Подведение итогов (Делимся впечатлениями от проведенного дня).

Обучение

В программе лагеря:
  • Занятия английским языком, единоборствами,
  • Выездные экскурсии,
  • Интенсивы по видеоблогингу и программированию,
  • Полноценное трехразовое питание,
  • Прогулки и игровые на свежем воздухе.

Расположение

Адрес: Россия, Санкт-Петербург, пер. Гривцова, д.3. открыть карту

Смены проходят по адресам:
1. Россия, Санкт-Петербург, пер. Гривцова, д.3.
2. Россия, Санкт-Петербург, пер. Красногвардейский, д.15Д

Питание

Трехразовое горячее питание, возможность приносить еду с собой для аллергиков.

Безопасность и медицина

Все работники лагеря прошли инструктажи по технике безопасности и основам первой медицинской помощи. Во время прогулки на 1 взрослого приходится не более 3 детей.

Об организации

Год основания:
2019 г.;
Взрослых на отряд:
4;
Детей в отряде:
25;
Детей на смене:
25;

Информация с официального сайта лагеря «SHIFT»

О сотрудниках

Все наши наставники — молодые и увлеченные педагоги. Благодаря энтузиазму, энергии и опыту они с легкостью могут заинтересовать детей тем, что любят сами.

  • Олег Суховский

    Наставник творческой мастерской

    В сфере образования с 2014 года. Начинал с помощника преподавателя в БГТУ «Военмех». В 2016 году основал сеть школ SHIFT. В 2017 году разработал собственную игровую методику обучения логической математике.

  • Евгения Кондрашина

    Наставник технической мастерской

    Преподает с 2014 года. Начинала с математических кружков «Фрактал». В 2016 году перешла в SHIFT. Автор методик по программированию и математике, обучение по которым прошли уже более 600 детей.

  • Юлия Цугленок

    Наставник языковой мастерской

    3 года училась в Швейцарии (College du Leman,Geneva) по программе IB (International Baccalaureate). Год обучалась в Америке в School of the Art Institute of Chicago. Сейчас учится в СПбГАСУ по программе архитектура. Английский преподает с 2015 года. Сейчас преподает в школе английского Don’t Speak.

  • Егор Камнев

    Наставник творческой мастерской

    Путь в преподавании начал со студенческого педагогического отряда «Солярис». Работает в SHIFT c осени 2018 года. Провел более 500 занятий с детьми.

  • Екатерина Крылова

    Наставник технической мастерской

    Преподает в SHIFT c 2017 года. Катя лучше всех умеет увлечь детей даже самой скучной темой. С 2018 года занимается не только проведением занятий в группах, но и ведет онлайн школу!

Отзывы

  • Я в принципе за то, чтобы ребёнок развивался везде и всегда, регулярно, на постоянной основе, вне зависимости от каникул и обстоятельств. На ваших занятиях мой сын получает знания, которые помогут ему в будущем, заряд положительных эмоций за счёт разнообразных и интересных форм обучения! Прежде, чем записать Никиту в лагерь, я спросила Его самого! Это не только мое личное решение, поэтому показательно, когда он без сомнения согласился.

    Ну и как меня могло не заинтересовать?! если бы лагерь был за городом, то ещё с большим удовольствием отправила бы и на более долгий срок!

    Юлия Зюбина, мама
    15 Августа 2018

  • Возможность освежить знания летом. Разнообразие направлений. Занятость и общение ребенка целый день. Лояльный подход к выбору времени пребывания в лагере.

    Алена Гвоздякова, мама
    26 Июля 2018

Что включено в стоимость

  • 5 дней пребывания.
  • 15 приемов пищи (полдня — 10 приемов пищи)
  • 15 часов занятий (полдня — 7. 5 часов занятий)
  • Прогулки.
  • Игротеки (полный день).
  • Встречи с приглашенными экспертами.

Стоимость и смены

На текущий момент мы не располагаем информацией о сменах данного лагеря. Подпишитесь на обновление информации, и мы сообщим вам о появлении выгодных предложений на этот лагерь.

Не решается алгебра/высшая математика?.. ПОМОЖЕМ! — @дневники: асоциальная сеть

Прежде чем задать вопрос, просмотрите список уже существующих. Возможно, что аналогичные проблемы уже решались. Воспользуйтесь поиском по дневнику или по списку @тем. Если по-прежнему не получилось решить, то:
0) Делаем информативный заголовок.
1) Пишем тематику задания.
2) Указываем: уровень сложности(школа-№класса/вуз), название работы(контрольная/домашняя), источник, крайний срок получения ответа (по московскому времени)
3) Выкладываем само задание или ссылку на него (рисунки ОБЯЗАТЕЛЬНО прячем под кат — вставляем рисунок, выделяем его и нажимаем кнопку MORE). Поскольку в сообществе ведется индексация и создается задачная база, то задание (кроме сопутствующих рисунков) обязательно приводить в текстовом формате. Это необходимо также во избежание исчезновения заданий при удалении картинок с хостинга. Используйте для набора формул формат Пользовательский скрипт для отображения формул (Подробный Help и Справочник по набору формул).
4 )Проставляем @темы.
5) ОБЯЗАТЕЛЬНО указываем свои попытки решения. Если не понятна только часть решения или есть идеи как решать, пишите о них. К геометрическим задачам желательно приложить чертежи, чтобы обсуждение не было голословным.
6) Не забывайте говорить волшебные слова «спасибо» и «пожалуйста»
7) Если вы выкладываете аналогичную просьбу на другом ресурсе, своевременно ставьте в известность о решении проблемы.
8) Категорически запрещено удалять выложенные задания или отдельные их позиции. Они могут пригодиться другим в качестве образца. Кроме того, в них вложен труд Решателей. Наказание — исключение из сообщества.
9) Просим помнить, что полные решения мы не даем, контрольные работы и типовые расчеты не решаем.
10)Не допускаются обращения к экспертам (Решателям) в приват (u-mail, ICQ, e-mail, Skype и проч.) с просьбами о помощи : вся помощь осуществляется исключительно на территории сообщества.
11) Категорически (вплоть до исключения из сообщества) запрещается выкладывать для решения задачи действующих олимпиад.
12) Запрещается использовать ненормативную лексику в текстах сообщений, подписях, никах и аватарах, оскорблять членов и гостей сообщества. Наказание — исключение из сообщества. Использование излишне откровенных аватаров (картинок) будет иметь аналогичные последствия.
13) Запрещается использование тегов, мешающих индексированию записей в поисковых системах. Наказание — исключение из сообщества.
14) Если решение задачи представлено в виде картинки или видео, то по просьбе решателя посетитель сообщества должен предоставить решение и в виде текста.
15) При оформлении информации о книжных новинках рекомендуется следовать советам, изложенным в этом топике.

Обращение к решателям


Просьба придерживаться концепции сообщества, то есть учить решать задачи. Пожалуйста, воздержитесь от полных готовых решений.
Желательными способами оказания помощи являются, в частности, следующие:
1. Объяснить первый шаг решения задачи, предложив восстановить дальнейший ход рассуждений самостоятельно.
2. Дать ссылки на теоретические факты, которые должны быть использованы в решении задачи.
3. Описать общий ход решения, опустив технические детали, которые автор вопроса может восстановить самостоятельно.

@дневники: l Shift->stop->end l — Не решается алгебра/высшая математика?.. ПОМОЖЕМ!

Список заданий викторины состоял из 36 вопросов. За каждый правильный ответ ученик получал 5 очков, за неправильный ответ с него списывали 11 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 75 очков, если известно, что по крайней мере один раз он ошибся?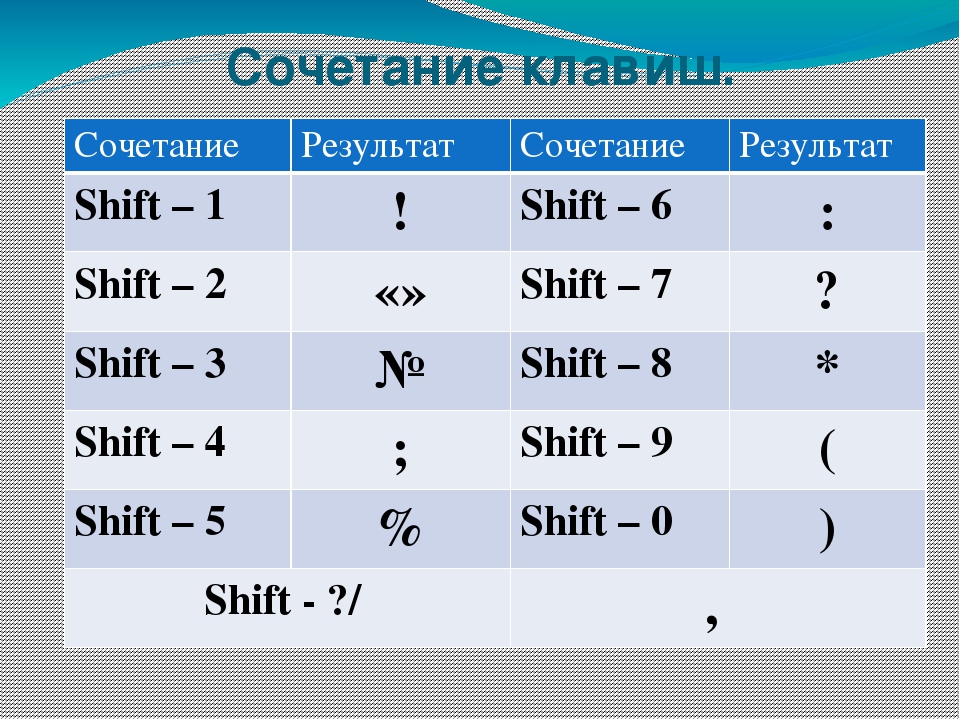

ЕГЭ 2020. Математика. Базовый уровень. 10 вариантов. Типовые тестовые задания от разработчиков ЕГЭ / А. В. Антропов, А. В. Забелин, Е. А. Семенко, Н. А. Сопрунова, С. В. Станченко, И. А. Хованская, Д. Э. Шноль, И. В. Ященко; под ред. И. В. Ященко. — М. : Издательство «Экзамен», 2020. — 64 с. (Серия «ЕГЭ. Тесты от разработчиков») ISBN 978-5-377-13925-6
Авторы пособия — ведущие специалисты, принимающие непосредственное участие в разработке методических материалов для подготовки к выполнению контрольных измерительных материалов ЕГЭ.
Книга содержит 10 вариантов комплектов типовых тестовых заданий по математике, составленных с учетом всех особенностей и требований Единого государственного экзамена по математике базового уровня. Назначение пособия — предоставить читателям информацию о структуре и содержании контрольных измерительных материалов по математике, степени трудности заданий. В сборнике даны ответы на все варианты тестов. Кроме того, приведены образцы бланков, используемых на ЕГЭ для записи ответов и решений.
Пособие может быть использовано учителями для подготовки учащихся к экзамену по математике в форме ЕГЭ, а также старшеклассниками — для самоподготовки и самоконтроля.


а) Решите уравнение `tg (pi+x) cos(pi/2-2x) = tg (5pi)/4.`
б) Укажите корни этого уравнения, принадлежащие отрезку `[ -(3pi)/2; 0].`

ЕГЭ 2020. Математика. Профильный уровень. 10 вариантов. Типовые тестовые задания от разработчиков ЕГЭ / И. В. Ященко, М. А. Волчкевич, И. Р. Высоцкий, Р. К. Гордин, П. В. Семёнов, О. Н. Косухин, Д. А. Фёдоровых, А. И. Суздальцев, А. Р. Рязановский, В. А. Смирнов, А. В. Хачатурян, С. А. Шестаков, Д. Э. Шноль; под ред, И. В. Ищенко. — М.: Издательство «Экзамен», 2020. _. 63, [1] с. (Серия <<ЕГЭ. ОФЦ. Тесты от разработчиков») ISBN 978-5-377-14490-8
Авторы пособия — ведущие специалисты, принимающие непосредственное участие в разработке методических материалов для подготовки к выполнению контрольных измерительных материалов ЕГЭ.
Типовые тестовые задания по математике содержат 10 вариантов комплектов заданий, составленных с учётом всех особенностей и требований Единого государственного экзамена по математике профильного уровня в 2020 году. Назначение пособия — предоставить читателям информацию о структуре и содержании контрольных измерительных материалов 2020 г. по математике профильного уровня, степени трудности заданий.
В сборнике даны ответы на все варианты тестов и приводятся решения всех заданий одного из вариантов. Кроме того, приведены образцы бланков, используемых на ЕГЭ для записи ответов и решений.
Пособие может быть использовано учителями для подготовки учащихся к экзамену по математике в форме ЕГЭ, а также старшеклассникамии выпускниками- для самоподготовки и самоконтроля.

alleng. Спасибо.

Построение геометрических фигур. Использование клавиши «Shift» при построении прямой, квадрата и окружности

Тема: «Построение геометрических фигур. Использование клавиши Shift при построении прямых, квадратов и окружностей»

Цели:

  • Образовательные:  
    • научить пользоваться клавишей Shift при построении прямых, квадратов и окружностей;
    • научить создавать рисунок из точных фигур.
  • Развивающие:
    • развитие познавательного интереса;
    • развитие  внимания;
    • формирование  компьютерной грамотности и потребности в приобретении знаний.
  • Воспитательные:
    • воспитание трудолюбия;
    • привитие учащимся навыков самостоятельности в работе.

Тип урока: комбинированный.

Оборудование урока:

  • компьютеры;
  • проектор;
  • экран
  • презентация «Использование клавиши Shift при построении прямых, квадратов и окружностей».

План урока.

  1. Сообщение темы и постановка целей урока — 8 мин.
  2. Актуализация знаний учащихся — 5 мин.
  3. Изучение нового материала — 8 мин.
  4. Практическая работа на компьютере — 20 мин.
  5. Подведение итогов урока — 3 мин.
  6. Домашнее задание — 1 мин.

ХОД УРОКА

I. Сообщение темы и постановка целей урока

1. Учитель: Ребята, каждый год в ночь с 31 декабря на 1 января к нам приходит самый любимый праздник детей и взрослых Новый год! Это очень веселый праздник и каждый житель нашей страны под бой часов загадывает желание, что бы он хотел получить, достичь в наступающем новом году.

Пусть будет добрым, безобидным,
Неустающим Новый год.
Пусть мягкий снег залечит раны,
Весенний луч растопит лед.
Как можно больше улыбайтесь,
Вам смех откроет чудеса,
И лишь одно лекарство — радость —
Пусть вам весь год слепит глаза.
Не замыкайтесь и в обиде,
Не проклинайте суету.
И каждый день ваш будет светел,
И каждый миг вам даст мечту.
И пусть вас новый ветер странствий
Закружит в зелени дорог,
Пусть растворитесь вы в пространстве,
Пусть красота собьет вас с ног.
Ищите, мучайтесь, решайтесь,
Лишь в этом жизни вечный свет.
Всем, что вокруг вас, восхищайтесь,
И вас не бросит счастье, нет.

Учитель: Ребята, скажите пожалуйста, а как вы в своей семье встречаете Новый год?
А вот послушайте как встречают новый год в других странах мира.
В традиции калмыков  встречать новый год 22 декабря, в зимний солнцеворот, начиная с которого день становится длиннее. Буряты отмечают Новый год по лунному календарю – в первое новолуние первого месяца весны, и называется он Сагаалган, или праздник Белого месяца. Чаще он выпадает на февраль. Китайцы празднуют Новый год между 17 января и 19 февраля во время новолуния. Адыгейцы, иранцы, афганцы, казахи встречают Новый год 21 и 22 марта, в день весеннего равноденствия, когда просыпается природа, и называется он Наурыз, или Навруз.
А вы знаете, что в России, в старину, Новый год встречали осенью – 1 сентября, после уборки урожая.
Ну и подведя всему вышесказанному итог сегодня на уроке мы с вами попытаемся нарисовать поздравительную открытку С Новым Годом.

II. Актуализация знаний учащихся

  1. С помощью какой программы можно создать поздравительную открытку? (Paint)
  2. Как запустить Paint? (Пуск – программы – стандартные – Paint)
  3. Какую панель необходимо использовать для создания изображения? (панель инструментов)
  4. Какими инструментами из названной панели вы уже владеете? (карандаш, кисть, распылитель, ластик, заливка, линия, прямоугольник и т. д)
  5. Какие действия надо воспроизвести, чтобы воспользоваться названными инструментами? (выбрать курсором мыши любой инструмент (сделать щелчок левой кнопки мыши),  перевести указатель мыши на рабочее поле,  передвигать указатель мыши в нужном направлен, нажав при этом левую кнопку мыши).

Учитель: Откройте графический редактор и нарисуйте с помощью инструментов рисования геометрические фигуры.
– Какие инструменты вы использования для этого?
– Скажите, а у вас с первого раза получилось нарисовать точный квадрат, прямую и окружность?
Так вот,  сегодня на уроке мы с вами должны научиться рисовать точные геометрические фигуры.

III. Изучение нового материала

Презентация ««Использование клавиши Shift при построении прямых, квадратов, окружностей». (Приложение 1)

  • Рисуя вспомогательные линии для пирамиды, вы, наверное,  заметили, как трудно нарисовать прямую горизонтальную линию. Однако графический редактор позволяет рисовать такие линии без особого труда. Для этого надо во время рисования держать нажатой клавишу Shift, левую или правую. Используйте ту, что удобнее.
  • Используя инструмент ЛИНИЯ с клавишей Shift, можно нарисовать строго горизонтальную, вертикальную и наклоненную точно под углом 450 линию.
  • Если рисовать инструментом ПРЯМОУГОЛЬНИК с нажатой клавишей Shift, то будут получаться квадраты. (Спросить у обучающихся что такое квадрат)
  • Клавишу Shift можно использовать и при рисовании инструментом ЭЛЛИПС. При нажатой клавише получаются круги.

IV. Практическая работа на компьютере

  1. Нарисуем поздравительную открытку С Новым Годом!
  2. Надпись С Новым Годом напишем с помощью КИСТИ.
  3. Дом и Снеговика будем рисовать с использованием клавиши Shift.
  4. Цветовую палитру выбираете по своему вкусу.

Учитель: Итак, с открытками закончили, а теперь, пожалуйста, посмотрите на открытку соседа и оцените его работу.

V. Подведение итогов урока

– Что нового вы  сегодня узнали  на уроке?
– С помощью какой клавиши можно рисовать точные геометрические фигуры?

VI. Домашнее задание

Учебник стр. 54, параграф 2.10.

что это такое. Знак косая черта / и \

Слэш (slash) – это знак косой черты, прямая линия, наклоненная вправо /. Такой знак используется в интернете, в системе Windows, программировании, математике и русском языке. Еще встречается обратная косая черта — бэкслеш \.

 

Как набрать слэш на клавиатуре

Изначально в русской клавиатуре не было этого символа, так как в основном он использовался в адресах интернета и программировании, а там нужно печатать только английскими буквами. Но со временем слеш и бэкслеш появились и в русской раскладке, так как стали использоваться в текстах.

Косая черта расположена на клавиатуре в нескольких местах:

  • Возле правой клавиши Shift на английской раскладке.
  • В цифровой части клавиатуры независимо от раскладки и регистра.
  • Над кнопкой Enter или слева от нее (набирать нужно вместе с Shift).

Обратная косая черта обычно находится слева или над кнопкой Enter. Также она может быть между левым Shift и буквой Z (Я).

Существуют альтернативный способ набора этих символов. Сначала нужно убедиться, что включен NumLock. Для этого просто попробуйте напечатать цифры через правую цифровую часть клавиатуры. Если они набираться не будут, тогда нужно нажать кнопку NumLock один раз.

Для печати косой черты зажимаем клавишу Alt и набираем на цифровой клавиатуре сначала 4 затем 7, после чего отпускаем Alt.

 

Обратный слэш \ можно поставить таким же способом, только вместо 4 и 7 набирать 9 и 2

Применение

В интернете. Используется в адресах интернет-ресурсов: имя любого сайта начинается с «http://» или «https://». В зависимости от вложенности страницы слешей будет больше (http://site.ru/category/category2/…), так как знак / является разделителем в адресе.

В русском языке. Заменяет предлоги «и», «или», а также обозначает единое сложное понятие, например: проблема конструктивных/деструктивных конфликтов, с целью покупки/продажи. Еще данный символ применяется при обозначениях каких-либо величин и их соотношений, как в полной, так и сокращенной формах, например: доллар/рубль, центнер/гектар, килограмм/метр.

В математике. Обозначает операцию деления и по значению приравнивается к двоеточию и горизонтальной черте.

Используется в этом значении в основном в компьютерных программах, например, в Excel.

Другие сферы применения. Еще слэш используется в программировании, а также является служебным типографским знаком и применяется при указании ссылок на литературные источники, разбиении текста на строки (цитировании стихов), обозначении дат.

Где используют бэкслеш

В математике. Означает разность множеств. Например, A\B на языке математики значит множество элементов, которые не входят в В, но входят в А.

В системе Windows. Употребляется при разделении каталогов, именно поэтому такой символ нельзя использовать в названиях файлов.

Например, путь в системе D:\Фото\2020\Прогулка означает, что нужно открыть папку «Прогулка», которая находится в папке «2020», а та, в свою очередь, в «Фото» на диске D.

Автор: Илья Кривошеев

Сочетания клавиш Mac, которые вы должны знать


Сочетания клавиш — блестящая экономия времени; гораздо проще нажать две или три клавиши одновременно, чем отправиться на охоту через вложенные меню. Но ярлыки зависят от знаний и мышечной памяти. Вы должны выделить время, чтобы изучить их, прежде чем вы сможете извлечь выгоду в долгосрочной перспективе.

Вот почему мы здесь. В этом руководстве по основным сочетаниям клавиш для пользователей Mac рассматриваются наиболее полезные комбинации горячих клавиш, которые сэкономят ваше время и стресс.

Три наиболее важные клавиши на вашем Mac находятся слева и справа от пробела (для правой и левой руки). К сожалению, эти ключи, кажется, вызывают больше путаницы, чем любые другие. Итак, наше руководство по быстрым клавишам начнется с выяснения тайны и объяснения того, что вы можете сделать с помощью Fn, Ctrl, Alt и Cmd.

Использование клавиши «Option» или «Alt» на Mac

Существует большая путаница в том, что Apple называет ключом Option. Если вы используете британскую клавиатуру, скорее всего, это называется клавишей Alt, поэтому неудивительно, что большинство людей не знают, где она находится.

Клавиша Alt (иначе опция) находится между Control и Command. Он имеет иконку в виде склона и провал с линией над ним.

Скорее всего, вы впервые услышите упоминание о Option, когда вы следуете руководству и пытаетесь что-то исправить на своем Mac. Клавиша Alt — это та, которую вы используете, если вы хотите выбрать загрузочный раздел при запуске компьютера, вы также нажимаете ее при вводе определенных символов на клавиатуре, таких как # (Alt-3) или ¢ (Alt-4).

Вот обзор скрытых символов, которые вы можете набирать, используя Alt (клавиши могут немного отличаться, если вы не используете британскую клавиатуру).

Клавиша Option также позволяет вам включить опцию Сохранить как в приложениях Mac.

Вам может быть интересно, можете ли вы использовать клавишу Alt вместе с Ctrl и Delete, чтобы закрыть не отвечающий Mac. Принудительный выход на Mac немного отличается от на компьютере: вот как принудительно выйти на Mac.

Как набирать €, #,… и © на Mac

  • Alt-2: знак евро (€)
  • Alt-3: знак хэша или хэштег (#) (иногда его называют знаком фунта)
  • Alt-двоеточие (Alt- 🙂 дает вам многоточие (…)
  • Alt-G: знак авторского права (©)

Вы также можете использовать Alt / Option, чтобы сделать следующее:

  • Кнопка Control-Alt-Command-Power: выход из всех приложений
  • Alt-Shift-Command-Q: выйти из своей учетной записи
  • Alt-Delete: Удалить слово слева от курсора
  • Alt-Left Arrow: переместите курсор в начало предыдущего слова, добавьте Shift, чтобы выделить текст
  • Alt-Right Arrow: переместите курсор в конец следующего слова. (Добавьте Shift, чтобы выделить текст)
  • Если вы выбираете большие разделы текста, вы можете сделать это, переместив курсор в конец раздела, который вы хотите выделить, и нажимая Alt-Shift-Up Arrow, пока весь текст не будет выделен. (Это работает только в некоторых приложениях)
  • Точно так же, Alt-Shift-Down Arrow позволяет выделить текст под курсором
  • Alt-Command-F откроет функцию поиска и замены, если она есть в вашем приложении
  • Alt-Command-T покажет или скроет панель инструментов
  • Alt-Command-C — это комбинация клавиш, которую нужно использовать, если вы хотите скопировать стиль или скопировать настройки форматирования в буфер обмена
  • А Alt-Command-V вставит эти настройки форматирования в текст, который вы хотите изменить.
  • Alt-Shift-Command-V вставит и сопоставит стиль — так, чтобы текст, в который вы вставляете, имел тот же стиль, что и текст вокруг него, а не стиль, перенесенный из места, из которого вы его скопировали
  • Alt-Command-D покажет или скроет Dock внизу экрана
  • В Finder Alt-Command-L — это удобный ярлык для открытия папки загрузок.
  • Также в Finder нажатие Alt-Command-P покажет путь, чтобы вы могли видеть точное местоположение того, что вы смотрите
  • Alt-Command-S покажет или скроет боковую панель в Finder
  • Alt-Command-N запустит новую умную папку в Finder
  • Если вы выбрали несколько файлов в Finder, вы можете нажать Alt-Command-Y, чтобы увидеть полноэкранное слайд-шоу этих файлов.
  • Для быстрого доступа к настройкам дисплея нажмите Alt-Brightness Up (или Brightness Down, также F1 или F2).
  • Вы можете открыть настройки управления полетами, нажав Alt-Mission Control (F3)
  • Чтобы дублировать / скопировать элемент в Finder или на рабочем столе, нажмите Alt при его перетаскивании.
  • Чтобы создать псевдоним (ярлык для файла), вы одновременно нажимаете Alt и Command при перетаскивании файла из местоположения в Finder в другое место, появится знак стрелки, указывающий, что это ссылка на файл, а не копия Это

Использование клавиши Command на Mac

Если вы думали, что путаница Alt и Option ставит в тупик, есть еще больше шансов запутаться, когда дело доходит до клавиши Command. У клавиши Command (cmd) есть наследие, которое приводит к путанице — многие старые пользователи Mac будут называть его ключом Apple, потому что в прошлом на нем раньше был логотип Apple, но этот логотип перестал появляться некоторое время назад, когда Если было решено, что на продуктах Apple слишком много логотипов Apple.

Логотип, который вы все еще найдете на этом ключе, выглядит как волнистый квадрат или цветок с четырьмя лепестками. Он был разработан Сьюзен Каре для оригинального iMac (и основан на скандинавской иконе для интересного места).

Клавиша Command (cmd) работает аналогично клавише Control на ПК. На Mac вы используете клавишу Command, а на ПК вы используете Control (или Ctrl).

Если вам интересно, почему Ctrl-B не выделил ваш текст жирным шрифтом, скорее всего, вы ранее были пользователем ПК и не понимали, что Command — это новый элемент управления. Вы можете найти это полезным: Как перейти с ПК на Mac: Полное руководство по переходу на Mac с ПК.

Вот несколько комбинаций клавиш, которые используют Command:

  • Command-B: жирный
  • Command-I: курсив
  • Command-Z: отменить
  • Command-Q: выход
  • Command-W: закрыть окно
  • Command-P: печать
  • Shift-Command-P: настройка страницы (для проверки того, как она будет печататься)
  • Command-S: сохранить
  • Shift-Command-S: сохранить как или дублировать документ
  • Command-A: выбрать все

Как скопировать и вставить на Mac

  1. Выберите текст, который вы хотите скопировать — быстрый способ сделать это — навести указатель мыши на слово и дважды щелкнуть мышью. После того, как текст выделен, вы можете перетаскивать мышь вверх или вниз или вниз, чтобы выбрать больше слов. В качестве альтернативы, если вы выбираете несколько слов, предложений или абзацев, вы можете щелкнуть в начале раздела, затем нажать клавишу Shift и щелкнуть в конце раздела.
  2. Нажмите Command-C, чтобы скопировать текст (или Command-X, если вы хотите «вырезать» текст из того места, где он находится в данный момент)
  3. Перейдите туда, куда вы хотите вставить текст и нажмите Command-V
  • Command-C: Копировать
  • Command-X: вырезать
  • Command-V: вставить

Есть много более полезных комбинаций клавиш, которые используют Command, включая:

  • Command-F: найти
  • Command-G: найти снова
  • Command-H: скрыть окна приложения, которое вы используете
  • Command-M: свернуть текущее окно и отправить его в док
  • Command-N: открыть новый документ
  • Command-W: закрыть текущее окно
  • Command-Space Bar: открыть окно поиска Spotlight
  • Command-Tab: переключение между открытыми приложениями
  • Shift-Command-3, чтобы сделать скриншот на Mac
  • Command-Comma (,): открыть настройки для используемого вами приложения.
  • Command-T: показать или скрыть окно шрифтов
  • Command-Left Arrow: переместить курсор в начало строки
  • Command-Right Arrow: переместить курсор в конец строки
  • Command-Up Arrow: переместить курсор в начало документа
  • Command-Down Arrow: переместить курсор в конец документа. (Нажмите shift, чтобы выделить текст между точкой вставки и местом назначения в каждом из этих сценариев)
  • Командная левая фигурная скобка: выровнять слева
  • Командно-правая фигурная скобка: выравнивание справа
  • Shift-Command- |: центр
  • Shift-Command-Minus sign: уменьшить размер шрифта
  • Shift-Command-Plus знак: увеличить размер шрифта
  • Shift-Command-Question mark: открыть меню справки
  • Если вы находитесь в Finder или в веб-браузере, или в любом другом приложении, которое поддерживает вкладки, Command-T откроет новую вкладку

В Finder вы можете попробовать следующее:

  • Command-D — дублировать файл
  • Command-E — выбросить объем
  • Command-F — поиск
  • Command-I — получить информацию
  • Shift-Command-D — открыть папку рабочего стола
  • Shift-Command-F — открыть папку «Все мои файлы»
  • Shift-Command-H — открыть домашнюю папку
  • Shift-Command-G — открыть окно «Перейти к папке»
  • Shift-Command-I — открыть диск iCloud
  • Command-K — подключиться к серверу
  • Shift-Command-K — просмотр сети
  • Command-L — сделать псевдоним
  • Shift-Command-O — открыть папку «Документы»
  • Shift-Command-R — ярлык для окна AirDrop
  • Command-Delete — отправляет выбранный элемент в корзину
  • Shift-Command-Delete — Очистить корзину (добавьте клавишу Alt, если вы не хотите видеть диалог подтверждения)

Использование клавиши управления на Mac

С клавишей Command, выполняющей работу на Mac, с клавишей Control на ПК, вы можете удивиться, почему на клавиатуре Mac также есть клавиша Control.

Наиболее распространенное использование Control — это имитация щелчка правой кнопкой мыши или при использовании коврика для мыши (поскольку у некоторых мышей Apple отсутствует опция щелчка правой кнопкой мыши).

Существует много других применений для Control при использовании с другими комбинациями клавиш, например:

  • Кнопка Control-Command-Power перезагрузит ваш Mac
  • Кнопка Control-Shift-Power: переводит ваш дисплей в спящий режим
  • Кнопка Control-Option-Command-Power: закрывает все ваши приложения и закрывает ваш Mac
  • Control-H: удалить символ слева
  • Control-D: удалить символ справа
  • Control-K: удалить текст от курсора до конца строки
  • Control-A: перейти к началу строки (подробнее здесь: Как найти End и Home на клавиатуре Mac)
  • Control-E: перейти к концу строки или абзаца
  • Control-F: двигаться вперед на один символ
  • Control-B: двигаться назад на один символ

Вы также можете использовать клавишу Control, чтобы добавить документ или папку в Dock. Перейдите в Finder и выберите элемент, который вы хотите добавить в Dock (или найдите его, используя Spotlight: Cmd-Space, или выберите его на рабочем столе). Затем нажмите Control-Shift-Command-T.

Что делают клавиши F на Mac?

Есть несколько других специфических для Apple клавиш (в зависимости от вашей клавиатуры):

  • F1 / F2: яркость вверх и вниз
  • F3: Управление полетом (для обзора всех запущенных приложений, группировки окон из одного приложения и ваших пространств)
  • F4: ярлык для всех приложений на вашем Mac
  • F10 / F11 / F12: Звук

Вы можете установить другие клавиши F для выполнения действий управления полетом. Перейдите в «Системные настройки»> «Управление полетом» и добавьте неиспользуемые клавиши F для выполнения таких функций, как «Показать рабочий стол» или «Панель инструментов».

Как печатать буквы с акцентом на Mac

Некоторые буквы могут быть набраны с акцентами сверху, как это é, ä, ö. Это легко сделать на Mac:

  1. Удерживайте букву на клавиатуре, пока не появится всплывающее меню со всеми опциями.
  2. У каждой опции акцента есть номер под ним, нажмите номер на клавиатуре, чтобы превратить букву в эту версию с акцентом, или нажмите мышью на букву с акцентом

Как печатать специальные символы, символы эмодзи и математики на Mac

Вы можете использовать Просмотрщик символов, чтобы найти специальные символы, эмодзи и математические символы.

Нажмите Command-Control-Space и по умолчанию вы увидите символы Emoji. Чтобы увидеть средство просмотра символов со специальными символами любого шрифта на вашем Mac, щелкните значок «Просмотр символов» в правом углу окна или в строке меню рядом со временем и датой.


Открыв просмотр символов, используйте боковую панель для просмотра различных категорий, таких как символы валют или математические символы, и дважды щелкните любой элемент в главном окне, чтобы вставить его в документ.

Вы также можете искать любую опцию, используя поле поиска в правом верхнем углу. Введите термин «кошка», чтобы найти все символы, похожие на кошку.

Средство просмотра символов постоянно размещено над всеми остальными окнами, поэтому вы можете продолжить ввод текста в приложении и просматривать средство просмотра символов в верхней части документа. Вы можете переключаться между маленькой и большой программой просмотра символов, используя значок справа от поля поиска.

Также можно добавить «Просмотр персонажа» в виде значка строки меню, что позволяет быстро получить к нему доступ из любого приложения. Откройте Системные настройки, выберите «Клавиатура»> «Клавиатура» и выберите «Показать клавиатуру». Просмотр персонажей в строке меню. Теперь вы можете щелкнуть значок «Просмотр персонажа» в строке меню и выбрать «Показать просмотр персонажа».

Как добавить эмодзи на Mac?

Как мы уже говорили выше, просто нажмите Command-Control-Space, и вы увидите коллекцию Emoji, которую вы можете использовать.

Если у вас открыт просмотр персонажей, вы найдете раздел Emoji на боковой панели.

Зачастую проще использовать поле поиска в средстве просмотра символов, чтобы найти символы эмодзи.

Если вы хотите узнать больше об использовании эмодзи, это может быть полезно: Как использовать эмодзи

Как просмотреть ярлыки на Mac

Одна из хитрых уловок при изучении сочетаний клавиш на Mac — это использование Keyboard Viewer. Включить Показать клавиатуру Средства просмотра символов в строке меню (в Системных настройках> Клавиатура> Клавиатура).

Теперь нажмите на иконку «Просмотр персонажа» в строке меню и выберите «Показать клавиатуру». Появится визуальное представление клавиатуры, и при нажатии клавиш они будут выделены. Если вы удерживаете клавиши Alt и Shift, в Keyboard Viewer отображаются все специальные символы на каждой клавише. Вы можете использовать это, чтобы узнать специальные символы на каждой клавише.


Комбинации клавиш для выключения или сна вашего Mac

  • Ctrl-Eject: Показать диалог перезагрузки / сна / выключения
  • Shift-Control-Eject: положит ваши дисплеи в режим сна
  • Command-Alt-Eject: переведет компьютер в спящий режим
  • Command-Control-Eject: сохранить / выйти из всех приложений, а затем перезапустить Mac
  • Command-Alt-Control-Eject: закрыть все приложения, а затем закрыть Mac
  • Command-Shift-Q: выйдите из своей учетной записи пользователя OS X (вас попросят подтвердить действие)
  • Command-Shift-Alt-Q: немедленно выйдите из учетной записи пользователя OS X (вас не попросят подтвердить действие)
  • Command-Alt-Esc: принудительный выход
  • Command-shift-Alt-Esc (в течение трех секунд): принудительное завершение самого переднего приложения

Читайте дальше: Как заблокировать Mac

Как использовать Application Switcher

Еще одна удобная комбинация клавиш — та, которая вызывает переключатель приложений. Это удобный способ перемещения между различными открытыми приложениями.

  • Command-Tab: перейти к следующему последнему использовавшемуся приложению из ваших открытых приложений
  • Command-Shift-Tab: перемещение назад по списку открытых приложений (отсортировано по недавнему использованию)
  • Command- ~ (тильда): переместиться назад по списку открытых приложений (только при активном переключателе приложений)

Если вы находите подобные вещи интересными, вы можете прочитать определения других технических терминов, относящихся к Apple, в нашем техническом жаргонном словаре пользователей Apple.

algorithm — Объяснение сегментации изображения с использованием Mean Shift

Основы сначала:

Сегментация по среднему сдвигу — это метод локальной гомогенизации, который очень полезен для демпфирования затенения или различий тональности в локализованных объектах. Пример лучше многих слов:

Действие: заменяет каждый пиксель средним числом пикселей в окрестности range-r, значение которого находится на расстоянии d.

Среднее смещение обычно занимает 3 входа:

  1. Функция расстояния для измерения расстояний между пикселями. Обычно евклидово расстояние, но может использоваться любая другая четко определенная функция расстояния. Манхэттенское расстояние иногда является еще одним полезным выбором.
  2. Радиус Все пиксели в пределах этого радиуса (измеренные в соответствии с вышеуказанным расстоянием) будут учтены для расчета.
  3. Разница в стоимости. Из всех пикселей внутри радиуса r мы возьмем только те, чьи значения находятся в пределах этой разницы для расчета среднего

Обратите внимание, что алгоритм не очень хорошо определен на границах, поэтому разные реализации приведут вас к разным результатам.

Я НЕ буду обсуждать здесь кровавые математические детали, поскольку их невозможно показать без правильной математической записи, недоступной в StackOverflow, а также потому, что их можно найти из хороших источников в других местах .

Давайте посмотрим на центр вашей матрицы:

153  153  153  153 
147  96   98   153 
153  97   96   147   
153  153  147  156

При разумном выборе радиуса и расстояния четыре центральных пикселя получат значение 97 (их среднее значение) и будут отличаться от соседних пикселей.

Давайте посчитаем это в Mathematica . Вместо того, чтобы показывать реальные цифры, мы будем отображать цветовую кодировку, чтобы было легче понять, что происходит:

Цветовая кодировка для вашей матрицы:

Затем мы берем разумное среднее смещение:

MeanShiftFilter[a, 3, 3]

И мы получаем:

Где все центральные элементы равны (до 97, кстати).

Вы можете повторить несколько раз с Mean Shift, пытаясь получить более однородную окраску. После нескольких итераций вы получите стабильную неизотропную конфигурацию:

В это время должно быть ясно, что вы не можете выбрать, сколько «цветов» вы получите после применения Mean Shift. Итак, давайте покажем, как это сделать, потому что это вторая часть вашего вопроса.

То, что вам нужно для того, чтобы заранее настроить количество выходных кластеров, это что-то вроде Kmeans clustering .

Это работает для вашей матрицы:

b = ClusteringComponents[a, 3]

{{1, 1, 1, 1, 1, 1, 1, 1}, 
 {1, 2, 2, 3, 2, 3, 3, 1}, 
 {1, 3, 3, 3, 3, 3, 3, 1}, 
 {1, 3, 2, 1, 1, 3, 3, 1}, 
 {1, 3, 3, 1, 1, 2, 3, 1}, 
 {1, 3, 3, 2, 3, 3, 3, 1}, 
 {1, 3, 3, 2, 2, 3, 3, 1}, 
 {1, 1, 1, 1, 1, 1, 1, 1}}

Или же:

Что очень похоже на наш предыдущий результат, но, как вы можете видеть, теперь у нас есть только три уровня выхода.

НТН!

Математические слова: Shift

индекс: нажмите на письмо
индекс: предметные области


эта страница обновлена 19-июл-17
Mathwords: Термины и формулы от алгебры I до исчисления
написаны, проиллюстрированы и веб-мастером Брюса Симмонса
Авторские права © 2000 Брюс Симмонс
Все права защищены

Объединить вертикальный и горизонтальный сдвиги

Теперь, когда у нас есть два преобразования, мы можем объединить их вместе. {- t} +1 \\ [/ latex], где [latex] k \\ [/ latex] — это процент мастерства, который может быть достигнут после практических занятий [latex] t \\ [/ latex].{-t} +1 \\ [/ латекс]

Мы можем нарисовать график, применяя эти преобразования по одному к исходной функции. Давайте проследим по двум пунктам через каждое из трех преобразований. Выберем точки (0, 1) и (1, 2).

  1. Сначала мы применяем горизонтальное отражение: (0, 1) (–1, 2).
  2. Затем мы применяем вертикальное отражение: (0, −1) (1, –2).
  3. Наконец, мы применяем вертикальный сдвиг: (0, 0) (1, 1).

Это означает, что исходные точки (0,1) и (1,2) становятся (0,0) и (1,1) после применения преобразований.{2} \\ [/ latex], граф [латекс] g \ left (x \ right) = — f \ left (x \ right) \\ [/ latex] и [латекс] h \ left (x \ right) = е \ влево (-x \ вправо) \\ [/ латекс]. Обратите внимание на любое неожиданное поведение этих функций.

Решение

Выполнение последовательности преобразований

При объединении преобразований очень важно учитывать порядок преобразований. Например, вертикальный сдвиг на 3, а затем вертикальное растяжение на 2 не создает такой же график, как вертикальное растяжение на 2, а затем вертикальный сдвиг на 3, потому что, когда мы сначала сдвигаем, как исходная функция, так и сдвиг растягиваются, в то время как только исходная функция растягивается, когда мы сначала растягиваем.

Когда мы видим такое выражение, как [latex] 2f \ left (x \ right) +3 \\ [/ latex], с какого преобразования мы должны начать? Ответ здесь хорошо следует из порядка операций. Учитывая выходное значение [latex] f \ left (x \ right) \\ [/ latex], мы сначала умножаем на 2, вызывая вертикальное растяжение, а затем прибавляем 3, вызывая вертикальный сдвиг. Другими словами, умножение перед сложением.

Горизонтальные преобразования сложнее представить. Когда мы пишем [latex] g \ left (x \ right) = f \ left (2x + 3 \ right) \\ [/ latex], например, мы должны думать о том, как входные данные функции [latex] g [/ latex] относятся к входам функции [latex] f \\ [/ latex]. Предположим, мы знаем [латекс] f \ left (7 \ right) = 12 \\ [/ latex]. Какой ввод в [latex] g \\ [/ latex] будет производить этот вывод? Другими словами, какое значение [latex] x \\ [/ latex] позволит [latex] g \ left (x \ right) = f \ left (2x + 3 \ right) = 12? \\ [/ latex] Нам понадобится [латекс] 2х + 3 = 7 \ [/ латекс]. Чтобы решить для [latex] x \\ [/ latex], мы сначала вычтем 3, что приведет к горизонтальному смещению, а затем разделим на 2, что приведет к горизонтальному сжатию.

С этим форматом очень сложно работать, потому что обычно намного проще растянуть график по горизонтали перед смещением.{2} \\ [/ латекс]

Теперь мы можем более отчетливо наблюдать сдвиг по горизонтали влево на 2 единицы и сжатие по горизонтали. Такой фактор позволяет нам сначала растянуть по горизонтали, а затем сместиться по горизонтали.

Общее примечание: объединение преобразований

При объединении вертикальных преобразований, записанных в форме [латекс] af \ left (x \ right) + k \\ [/ latex], сначала растяните по вертикали на [латекс] a \\ [/ latex], а затем сдвиньте по вертикали на [латекс ] к \\ [/ латекс].

При объединении горизонтальных преобразований, записанных в форме [латекс] f \ left (bx + h \ right) \\ [/ latex], сначала сдвинуть по горизонтали на [латекс] h [/ latex], а затем растянуть по горизонтали на [латекс] \ гидроразрыв {1} {b} \\ [/ latex].

При объединении горизонтальных преобразований, записанных в форме [латекс] f \ left (b \ left (x + h \ right) \ right) \\ [/ latex], сначала растяните по горизонтали на [латекс] \ frac {1} {b } [/ latex], а затем сдвинуть по горизонтали на [latex] h \\ [/ latex].

Горизонтальные и вертикальные преобразования независимы. Не имеет значения, какие преобразования выполняются в первую очередь: по горизонтали или по вертикали.

Пример 19: Нахождение тройного преобразования табличной функции

Учитывая приведенную ниже таблицу для функции [latex] f \ left (x \ right) \\ [/ latex], создайте таблицу значений для функции [latex] g \ left (x \ right) = 2f \ left ( 3х \ вправо) +1 \\ [/ латекс].

[латекс] x [/ латекс] 6 12 18 24
[латекс] f \ слева (x \ справа) [/ латекс] 10 14 15 17

Решение

Это преобразование состоит из трех этапов, и мы будем работать изнутри. Начиная с горизонтальных преобразований, [latex] f \ left (3x \ right) [/ latex] — это горизонтальное сжатие с помощью [latex] \ frac {1} {3} \\ [/ latex], что означает, что мы умножаем каждый [ latex] x \ text {-} \\ [/ latex] значение по [latex] \ frac {1} {3} \\ [/ latex].

[латекс] x [/ латекс] 2 4 6 8
[латекс] f \ слева (3x \ справа) [/ латекс] 10 14 15 17

Теперь, глядя на вертикальные преобразования, мы начинаем с вертикального растяжения, которое умножает выходные значения на 2. Мы применяем это к предыдущему преобразованию.

[латекс] x \ [/ латекс] 2 4 6 8
[латекс] 2ф \ левый (3х \ правый) \ [/ латекс] 20 28 30 34

Наконец, мы можем применить вертикальный сдвиг, который добавит 1 ко всем выходным значениям.

[латекс] x \ [/ латекс] 2 4 6 8
[латекс] g \ left (x \ right) = 2f \ left (3x \ right) +1 \\ [/ latex] 21 29 31 35

Пример 20: Нахождение тройного преобразования графа

Используйте график [латекс] f \ left (x \ right) \\ [/ latex], чтобы нарисовать график [латекса] k \ left (x \ right) = f \ left (\ frac {1} {2 } x + 1 \ right) -3 \\ [/ latex].

Рисунок 27

Решение

Для упрощения давайте начнем с выделения внутренней части функции.

[латекс] f \ left (\ frac {1} {2} x + 1 \ right) -3 = f \ left (\ frac {1} {2} \ left (x + 2 \ right) \ right) — 3 \ [/ латекс]

Разложив внутреннюю часть на множители, мы можем сначала растянуть по горизонтали на 2, на что указывает [latex] \ frac {1} {2} \\ [/ latex] внутри функции. Помните, что удвоенный размер 0 по-прежнему равен 0, поэтому точка (0,2) остается в (0,2), а точка (2,0) растягивается до (4,0).

Рисунок 28

Затем мы сдвигаем по горизонтали влево на 2 единицы, как указано [latex] x + 2 \\ [/ latex].

Фиг.29

Наконец, мы сдвигаемся по вертикали на 3, чтобы завершить наш эскиз, на что указывает [latex] -3 \\ [/ latex] снаружи функции.

Фиг.30

Амплитуда, период, фазовый сдвиг и частота

Некоторые функции (например, синус и косинус) повторяются вечно
и называются периодическими функциями .

Период переходит от одного пика к следующему (или от любой точки до следующей точки совпадения):

Амплитуда — это высота от центральной линии до пика (или до впадины). Или мы можем измерить высоту от самой высокой до самой низкой точки и разделить ее на 2.

Фазовый сдвиг показывает, насколько функция сдвинута на горизонтально на от обычного положения.

Вертикальный сдвиг показывает, насколько функция сдвинута на по вертикали на от обычного положения.

Теперь все вместе!

У нас может быть все в одном уравнении:

y = грех (B (x + C)) + D

  • амплитуда A
  • период равен 2π / B
  • фазовый сдвиг C (положительный левый )
  • вертикальный сдвиг D

А вот как это выглядит на графике:

Обратите внимание, что здесь мы используем радианы, а не градусы, а полный оборот равен 2π радианам.

Пример: sin (x)

Это основная неизмененная формула синуса. A = 1, B = 1, C = 0 и D = 0

Итак, амплитуда 1 , период 2π , нет сдвига фазы или вертикального сдвига:

Пример: 2 sin (4 (x — 0,5)) + 3

  • амплитуда A = 2
  • период 2π / B = 2π / 4 = π / 2
  • сдвиг фазы = -0.5 (или 0,5 вправо)
  • вертикальный сдвиг D = 3

Прописью:

  • 2 говорит нам, что он будет в 2 раза выше, чем обычно, поэтому Amplitude = 2
  • , обычный период равен 2 π , но в нашем случае он «ускорен» (укорачивается) 4 в 4 раза, поэтому Период = π / 2
  • и −0,5 означает, что он будет смещен вправо на 0.5
  • , наконец, +3 сообщает нам, что центральная линия y = +3, поэтому вертикальный сдвиг = 3

Вместо x мы можем иметь t (для времени) или, возможно, другие переменные:

Пример: 3 sin (100t + 1)

Сначала нам нужны скобки вокруг (t + 1), поэтому мы можем начать с деления 1 на 100:

3 sin (100t + 1) = 3 sin (100 (t + 0,01))

Теперь мы видим:

  • амплитуда A = 3
    • Период
  • равен 2π / 100 = 0. 02 π
  • фазовый сдвиг C = 0,01 (влево)
  • вертикальный сдвиг составляет D = 0

И получаем:

Частота

Частота — это то, как часто что-то происходит в единицу времени (на «1»).

Пример: Здесь функция синуса повторяется 4 раза от 0 до 1:

Итак, частота равна 4

И Период 1 4

Фактически Период и Частота связаны:

Частота = 1 Период

Период = 1 Частота

Пример из предыдущего: 3 sin (100 (t + 0.01))

Период 0,02 π

Итак, частота 1 0,02π знак равно 50 π

Еще несколько примеров:

Период Частота
1 10 10
1 4 4
1 1
5 1 5
100 1 100

Когда частота составляет в секунду , это называется «Герц».

Пример: 50 Гц означает 50 раз в секунду


Чем быстрее он отскакивает, тем больше у него «Герц»!

Анимация

Ключевые сдвиги в математике | Common Core State Standards Initiative

Введение

Общие основные государственные стандарты по математике основаны на лучших из существующих стандартов и отражают навыки и знания, которые потребуются студентам для успешной учебы в колледже, карьеры и жизни.Понимание того, чем стандарты отличаются от предыдущих стандартов — и необходимых изменений, к которым они призывают — имеет важное значение для их внедрения.

Следующие ключевые сдвиги вызваны Common Core:

  1. Больше Фокус на меньшем количестве тем

    Common Core требует большего внимания к математике. Вместо того, чтобы стремиться охватить множество тем в учебной программе шириной в милю и глубиной в дюйм, стандарты просят учителей математики значительно сузить и углубить то, как время и энергия тратятся в классе. Это означает глубокое сосредоточение на основной работе каждой ступени, а именно:

    • В классах K – 2: Понятия, навыки и решение задач, связанных со сложением и вычитанием
    • Для 3–5 классов: Понятия, навыки и решение задач, связанных с умножением и делением целых чисел и дробей
    • В 6 классе: Соотношения и пропорциональные отношения, а также ранние алгебраические выражения и уравнения
    • В 7 классе: Соотношения и пропорциональные отношения, арифметика рациональных чисел
    • В 8 классе: Линейная алгебра и линейные функции

    Этот курс поможет учащимся получить прочную основу, включая твердое понимание концепций, высокую степень процедурных навыков и беглости, а также способность применять математические знания, которые они знают, для решения задач в классе и за его пределами.

  2. Согласованность : объединение тем и мышления в разных классах

    Математика — это не список разрозненных тем, трюков или мнемоник; это согласованная совокупность знаний, состоящая из взаимосвязанных концепций. Таким образом, стандарты разработаны с учетом последовательного перехода от класса к классу. Обучение тесно связано между классами, чтобы учащиеся могли построить новое понимание на основе, заложенной в предыдущие годы. Например, в классе 4 -го учащиеся должны «применить и расширить предыдущее понимание умножения, чтобы умножить дробь на целое число» (Стандарт 4.NF.4). Это распространяется на 5 -й класс , когда ожидается, что учащиеся будут развивать этот навык, чтобы «применять и расширять предыдущее понимание умножения для умножения дроби или целого числа на дробь» (Стандарт 5.NF.4). Каждый стандарт — это не новое событие, а продолжение предыдущего обучения.

    Согласованность также встроена в стандарты в том, как они усиливают основную тему в классе с помощью вспомогательных дополнительных тем. Например, вместо того, чтобы представлять тему отображения данных как самоцель, эта тема используется для поддержки словесных задач на уровне своего класса, в которых учащиеся применяют математические навыки для решения задач.

  3. Строгость : стремиться к концептуальному пониманию, процедурным навыкам, беглости и применению с равной интенсивностью

    Строгость означает глубокое, подлинное владение математическими понятиями, не усложняя математику и не вводя темы в более ранние классы. Чтобы помочь учащимся соответствовать стандартам, преподаватели должны будут с равной интенсивностью придерживаться трех аспектов строгости в основной работе каждого класса: концептуальное понимание, процедурные навыки и беглость, а также применение.

    Концептуальное понимание: Стандарты требуют концептуального понимания ключевых понятий, таких как числовая стоимость и соотношения. Студенты должны иметь возможность получить доступ к концепциям с разных точек зрения, чтобы рассматривать математику как нечто большее, чем набор мнемоник или дискретных процедур.

    Процедурные навыки и беглость: Стандарты требуют скорости и точности в расчетах. Студенты должны практиковать основные функции, такие как однозначное умножение, чтобы иметь доступ к более сложным концепциям и процедурам. Беглость речи должна быть решена в классе или с помощью вспомогательных материалов, поскольку некоторым студентам может потребоваться больше практики, чем другим.

    Заявление: Стандарты призывают учащихся использовать математику в ситуациях, требующих математических знаний. Правильное применение математических знаний зависит от наличия у студентов твердого концептуального понимания и беглости процедур.

предварительное вычисление алгебры — Объяснение горизонтального сдвига и масштабирования

Enter, Функциональная Обезьяна…

Как описано в ссылке, чтобы построить график, просто представьте ось $ x $, покрытую кокосами, по одной на каждое значение $ x $, например:

$$ \ cdots \ quad (-3 \;) \ quad \ color {# 9509A5} {(- 2 \;)} \ quad \ color {green} {(\; — 1 \;)} \ quad \ color {красный} {[\; 0 \;]} \ quad \ color { # 2B87CD} {(\; 1 \;)} \ color {# D86907} {\ quad (\; 2 \;)} \ quad (\; 3 \;) \ quad \ cdots $$

с «$ \ color {red} {[\; \ cdot \;]} $», обозначающим кокос в начале координат. Обезьяна-функция прогуливается по оси, поднимает каждый кокос $ x $, оценивает соответствующее значение $ y $ (как и обычно) и бросает кокос на соответствующую высоту (или глубину).График построен!

Но подождите! Никто никогда не говорил, что значения кокосов равны , требуются , чтобы соответствовать значениям координат $ x $, которые были раскрашены для удобства. Хмммм …

Если кокос в (окрашенном) месте $ x $ имеет значение $ x + 1 $, то ряд кокосов выглядит следующим образом: $$ \ cdots \ quad (-2 \;) \ quad \ color {# 9509A5} {(\; — 1 \;)} \ quad \ color {green} {(\; 0 \;)} \ quad \ color {красный} {[\; 1 \;]} \ quad \ color { # 2B87CD} {(\; 2 \;)} \ color {# D86907} {\ quad (\; 3 \;)} \ quad (\; 4 \;) \ quad \ cdots $$

Важно отметить, что кокос локаций по цвету не изменился.Кокосы по-прежнему находятся на оси в местах $ x = \ cdots, -3, \ color {# 9509A5} {- 2}, \ color {green} {- 1}, \ color {red} {0}, \ color {# 2B87CD} {1}, \ color {# D86907} {2}, 3, \ cdots $ по-прежнему указывает на кокос в исходной точке .

Что касается Function Monkey, добавление $ 1 к каждому значению кокоса фактически привело к сдвигу строки кокосов влево на . (Аналогичным образом, добавление $ -1 $ к каждому значению кокоса эффективно сдвигает ряд кокосов вправо.) Поскольку Function Monkey бросает кокосы вертикально, построенный график сдвигается таким же образом.

Аналогичным образом умножение каждой (исходной) стоимости кокоса на $ 2 $ дает следующую строку кокосов:

$$ \ cdots \ quad (-6 \;) \ quad \ color {# 9509A5} {(- 4 \;)} \ quad \ color {green} {(- 2 \;)} \ quad \ color {красный } {[\; 0 \;]} \ quad \ color { # 2B87CD} {(\; 2 \;)} \ color {# D86907} {\ quad (\; 4 \;)} \ quad (\; 6 \;) \ quad \ cdots $$

Опять же, местоположений кокосов не изменились, но мы видим, что диапазон значений кокоса от -6 $ до 6 $ был сжат в пространство между местоположениями $ x = -3 $ и $ x = 3 $.На графике будет такое же сжатие по горизонтали.

Бессюжетный способ размышления об этом, который близок к вашей интерпретации «старта», заключается в том, что «$ f (x + 1) $» обманывают Function Monkey $ f $, заставляя думать, что каждое входное значение является на одну единицу больше, чем есть на самом деле. Точно так же «$ f (2x) $» обманывает его, заставляя думать, что каждый ввод вдвое больше фактического размера. Эффективные изменения выходных значений соответствуют измененному восприятию Функциональной Обезьяны.

Сдвиг и масштабирование функции

Как сдвигать и масштабировать функции

У нас есть функция, и с помощью некоторых простых операций мы можем сдвинуть функцию по осям x и y, а также масштабировать ее (сжать и увеличить).

Давайте воспользуемся многочленом второй степени для этого примера:.

График этой функции выглядит так:

Мы можем добавить к функциям некоторые константы, которые позволят нам сдвигать и масштабировать его:. В нашем случае мы начинаем с того, что позволяем и быть 1, и и быть 0, что дает нам то же самое.

Изменение функции

Сначала сдвинем функцию по оси y. Это соответствует изменению константы. Добавляя к функции, мы перемещаем ее вверх и вниз.Воспользуемся и в качестве примера. Получаем функции и. На следующем графике показано, как функция смещается вниз для отрицательного значения и вверх для положительного значения (красная функция — исходная функция для справки):

Теперь давайте сдвинем функцию по оси x. Это соответствует изменению константы. В этом случае положительное значение сдвинет функцию влево, а отрицательное значение — вправо. Опять же, давайте использовать и, чтобы получить функции и.Сначала может показаться нелогичным, что положительное число смещается влево, но подумайте об этом так: когда вы находитесь в точке, а затем, добавляя положительное значение, скажем 2, мы оцениваем функцию в том месте, где оно должно быть. Таким образом, значение функции из было перемещено влево в. На следующем графике показано смещение функции:

Масштабирование функции

Масштабирование означает уменьшение или увеличение функции. Если мы масштабируем его по оси Y с коэффициентом 10, то там, где раньше значение функции было 10, теперь будет 100.Масштабирование по оси x с коэффициентом 10 означает, что значение функции теперь равно). Таким образом, все, что находится слева от начала координат, смещается дальше влево, а все, что находится справа, смещается дальше вправо.

Во-первых, давайте масштабируем по оси y. Это соответствует константе. Мы просто умножаем значение функции на какое-то число. Число больше единицы увеличивает функцию, а число от 0 до 1 сокращает ее в направлении y. Отрицательное значение также будет отражать функцию по оси x.Давайте использовать коэффициент масштабирования и отрицательное значение. Это дает нам функции:, и. Давайте посмотрим на график этих функций:

Теперь давайте масштабируем по оси x. Это соответствует константе. Значение больше единицы сжимает функцию, а значение от 0 до 1 увеличивает ее по оси x. Опять же, отрицательное значение также будет отражать функцию по оси Y, но поскольку наша функция в нашем примере является симметричной, она выглядела бы так же, если бы она была отражена.При тех же значениях и получаем и График выглядит так:

Комбинация сдвига и масштабирования

Конечно, можно использовать все комбинации сдвига и масштабирования. Давайте использовать для этого примера синусоидальную функцию. Мы используем все наши константы и устанавливаем их равными двум, так что мы получаем функцию. Для справки мы показываем нормальную синусоидальную функцию красным цветом, а наша новая функция — синим.

Мы видим, что функция сдвинута вверх на 2 (вдоль y), ее фаза сдвинута на 2 (вдоль x), ее амплитуда увеличена на 2 (вдоль y), а ее частота увеличена на 2 (вдоль x) .

Логический против. Арифметический сдвиг — Open4Tech

Логический сдвиг и Арифметический сдвиг — это операции манипулирования битами (побитовые операции).

Логический сдвиг
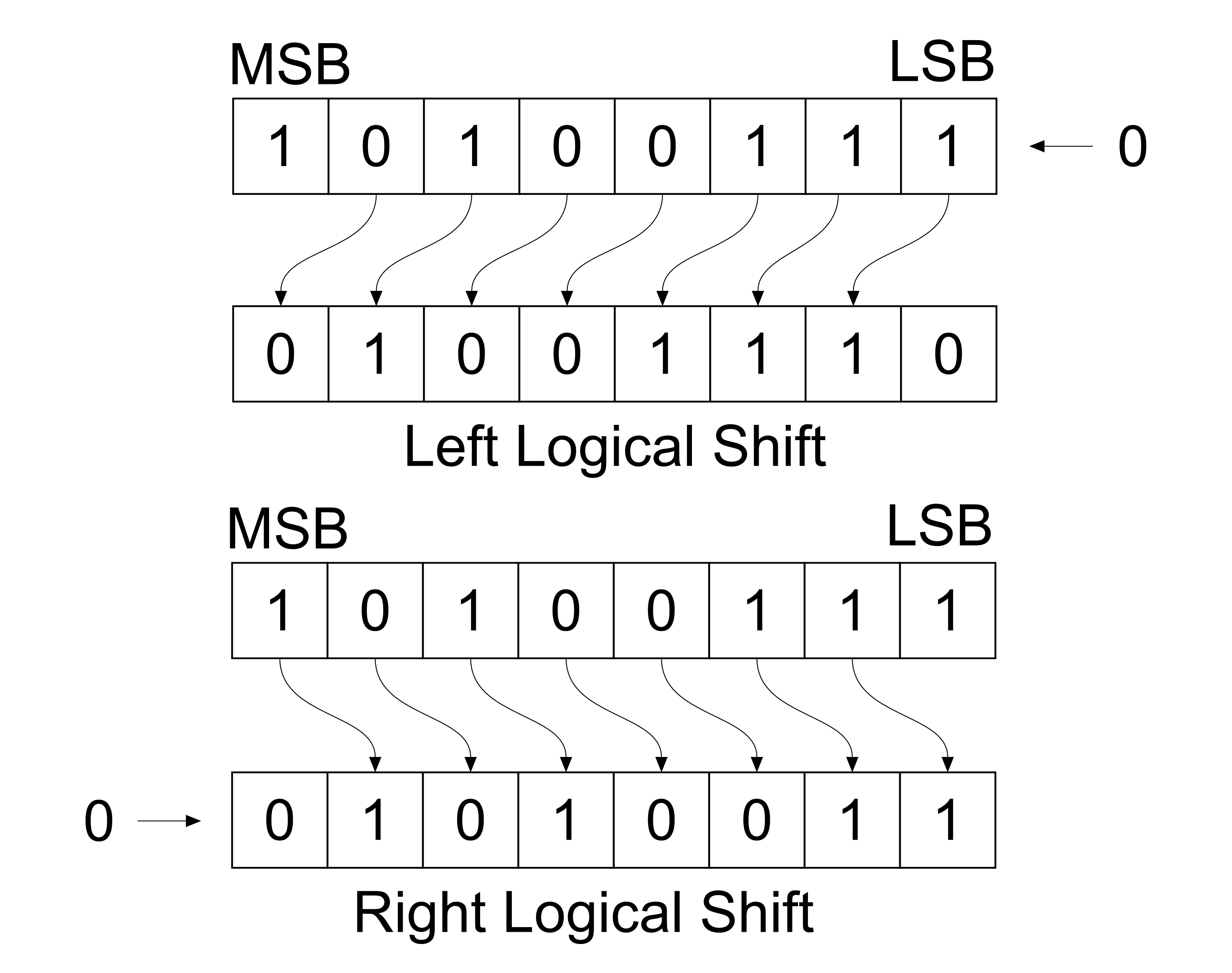
  • A Логический сдвиг влево одной позиции перемещает каждый бит влево на один. Свободный младший значащий бит (LSB) заполняется нулем, а самый старший бит (MSB) отбрасывается.
  • A Логический сдвиг вправо одной позиции перемещает каждый бит вправо на один.Младший значащий бит отбрасывается, а свободный старший бит заполняется нулем.

Рис. 1 Логический сдвиг на один бит

Арифметический сдвиг
  • A Левый арифметический сдвиг одной позиции перемещает каждый бит влево на один. Свободный младший значащий бит (LSB) заполняется нулем, а самый старший бит (MSB) отбрасывается. Он идентичен левому логическому сдвигу.
  • A Правый арифметический сдвиг одной позиции перемещает каждый бит вправо на один.Младший значащий бит отбрасывается, а свободный старший бит заполняется значением предыдущего (теперь сдвинутого на одну позицию вправо) старшего бита.

Рис. 1 Арифметический сдвиг влево и вправо на один бит

Операции арифметического сдвига можно использовать для деления или умножения целочисленной переменной.

Умножение на сдвиг влево:

Результатом операции сдвига влево является умножение на 2 n , где n — количество сдвинутых битовых позиций.

Пример:

Возьмем десятичное число 2, представленное как 4-битное двоичное число 0010 . Сдвинув влево на одну позицию, мы получим 0100 , что равно 4 в десятичном представлении. Если мы сдвинем его еще раз, мы получим двоичное значение 1000 , которое в десятичном представлении равно 8.

Для представления без знака, когда первая «1» сдвинута с левого края, операция переполнилась. Результат умножения больше максимально возможного.

Сдвиг влево для значений со знаком также работает, но происходит переполнение, когда наиболее значимый бит изменяет значения (с 0 на 1 или с 1 на 0).

Leave a comment