Знак больше меньше в какую сторону смотрит. Запоминаем знаки «больше» и «меньше»! Простейший способ
Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как знак больше и знак меньше , а также знак равно.
Однако, если с последним что-то напутать достаточно сложно, то о том, как и в какую сторону пишутся знаки больше и меньше (знак менее и знак более , как ещё их иногда называют) многие сразу после этой же школьной скамьи и забывают, т.к. они довольно редко используются нами в повседневной жизни.
Но практически каждому рано или поздно всё равно приходится столкнуться с ними, и «вспомнить» в какую сторону пишется нужный им символ получается лишь обратившись за помощью к любимой поисковой системе. Так почему бы не ответить развернуто на этот вопрос, заодно подсказав посетителям нашего сайта как запомнить правильное написание этих знаков на будущее?
Именно о том, как правильно пишется знак больше и знак меньше мы и хотим напомнить вам в этой небольшой заметке.
Перейдем сразу к делу. Если вам не очень интересно запоминать всё это на будущее и проще в следующий раз снова «погуглить», а сейчас просто нужен ответ на вопрос «в какую сторону писать знак», тогда для вас мы приготовили краткий ответ — знаки больше и меньше пишутся так, как показано на изображении ниже.
А теперь расскажем немного подробнее о том, как это понять и запомнить на будущее.
В общем и целом логика понимания очень проста — какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону — такой и знак. Соответственно, знак больше влево смотрит широкой стороной — большей.
Пример использования знака больше:
- 50>10 — число 50 больше числа 10;
- посещаемость студента в этом семестре составила >90% занятий.

Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной — меньшей, то перед вами знак меньше.
- 100
- на заседание явилось
Как видите, все довольно логично и просто, так что теперь вопросов о том, в какую сторону писать знак больше и знак меньше в будущем у вас возникать не должно.
Знак больше или равно/меньше или равно
Если вы уже вспомнили, как пишется необходимый вам знак, то дописать к нему одну черточку снизу вам не составит труда, таким образом вы получите знак «меньше или равно» или знак «больше или равно» .
Однако относительно этих знаков у некоторых возникает другой вопрос — как набрать такой значок на клавиатуре компьютера? В результате большинство просто ставят два знака подряд, к примеру, «больше или равно» обозначая как

На самом деле для того, чтобы напечатать эти знаки, существуют специальные символы, которые можно ввести на любой клавиатуре. Согласитесь, знаки «≤» и «≥» выглядят значительно лучше.
Знак больше или равно на клавиатуре
Для того, чтобы написать «больше или равно» на клавиатуре одним знаком даже не нужно лезть в таблицу специальных символов — просто поставьте знак больше с зажатой клавишей «alt» . Таким образом сочетание клавиш (вводится в английской раскладке) будет следующим.
Или же вы можете просто скопировать значок из этой статьи, если вам нужно воспользоваться им один раз. Вот он, пожалуйста.
≥
Знак меньше или равно на клавиатуре
Как вы наверное уже смогли догадаться сами, написать «меньше или равно» на клавиатуре вы можете по аналогии со знаком больше — просто поставьте знак меньше с зажатой клавишей «alt» . Сочетание клавиш, которое нужно вводить в английской раскладке, будет следующим.
Или просто скопируйте его с этой страницы, если вам так будет проще, вот он.
≤
Как видите, правило написания знаков больше и меньше довольно просто запомнить, а для того чтобы набрать значки больше или равно и меньше или равно на клавиатуре достаточно просто нажать дополнительную клавишу — всё просто.
Наряду с арифметическими действиями происходит знакомство с такими абстрактными понятиями, как «больше», «меньше» и «равно». Определить, с какой стороны больше предметов, а с какой – меньше, ребенку не составит особого труда. Но вот постановка знаков порой вызывает затруднения. Усвоить знаки помогут игровые методы.
«Голодная птичка»
Для игры понадобится знак – раскрытый клюв (знак «больше»). Его можно вырезать из картона или сделать большую модель из одноразовой тарелки. Чтобы заинтересовать малыша, можно приклеить или дорисовать глаза, перья, а рот сделать открывающимся
Объяснение начинается с предыстории: «Эта птичка – невеличка, любит хорошо покушать. Причем выбирает она всегда ту кучку, в которой больше еды».
После этого наглядно показывается, что птичка открывает клюв в сторону, где больше предметов.
Далее полученная информация закрепляется: на столе выкладываются кучки с зернышками, а ребенок определяет, в какую сторону птичка повернет свой клюв . Если не удастся правильно расположить его с первого раза, нужно помочь, еще раз проговорив, что рот открыт в сторону большего количества еды. Затем можно предложить еще несколько аналогичных заданий: числа написаны на листе, нужно правильно приклеить клюв.
Примеры можно разнообразить, заменив птичку щукой, крокодилом или любым другим хищником, который также разевает пасть в сторону большего числа.
Могут попасться необычные ситуации, где количество предметов в обеих кучках будет равное. Если ребенок это заметит – значит, внимательный.
За это нужно обязательно похвалить , а потом показать 2 одинаковые полоски и объяснить, что они такие же одинаковые, как и число предметов в кучках, а раз количество предметов равное, то и знак называется «равно».
Стрелочки
Маленькому школьнику можно объяснить знаки на основе сравнения их со стрелками, показывающими в разные стороны.
Сложности могут возникнуть при чтении выражений. Но и эта трудность преодолима: правильно поставив знак, он сможет правильно прочитать выражение
Упражнения на закрепление
После объяснения правил постановки знака необходимо потренироваться в выполнении аналогичных заданий.
С этой целью подойдут задания такого типа:
- «Поставь знак» (4 и 5 – нужен знак «меньше»).
- «Больше-меньше» — ребенок большим и указательным пальцами обеих рук показывает знаки, сравнивая размеры различных предметов или их количество (самолет больше стрекозы, земляника меньше арбуза).
- «Какое число» — стоят знаки, написано число с одной стороны, нужно догадаться, какое число будет с другой стороны (в выражении «_
- «Допиши числа» — нужно правильно поставить числа слева и справа от указанного знака (число 8 будет стоять слева от знака «больше», а число 2 – справа).

Для развития логики и мышления можно дополнить упражнения такими заданиями:
- «С какой стороны убежал предмет?» — слева нарисовано 3 треугольника, справа – 2 квадрата, а между ними стоит знак «=». Ребенок должен догадаться, что справа не хватает квадрата, чтобы равенство было верным. Если не получается это сделать сразу, можно решить задачу практически, добавив сначала слева треугольник, а затем – справа квадрат.
- «Что нужно сделать, чтобы неравенство стало правильным?» — с учетом ситуации ребенок определяет, с какой стороны нужно убрать или добавить предметы, чтобы знак стоял правильно.
Видео инфоурок расскажет о знаках: больше, меньше и равно
Класс: 1
Цели урока:
- Образовательная: познакомить со знаками меньше «», равно «=» и записями вида 22, 4=4, повторить геометрический материал, состав чисел;
- Развивающая: развитие коммуникативных качеств личности (умение работать в паре, вести учебный диалог, проводить самооценку)
- Воспитательная: воспитание чувства сопереживания, взаимопомощи.

1. Орг. момент
Внимание, проверь дружок,
Готов ли ты начать урок?
Всёли на месте, всёли в порядке
Книга, ручка и тетрадки?
И цветные карандаши
Ты на парту положи,
И линейку не забудь
В математику держим путь!А сейчас, ребята, поудобнее садитесь,
Не шумите, не вертитесь,
И внимательно считайте
А спрошу вас – отвечайте.
Вам условие понятно?
Это слышать мне приятно
Путешествие зовёт
Первоклашек на урок!
2. Основная часть:
Учитель: А совершим мы с вами сегодня полёт в неизведанное космическое пространство. Сегодня мы будем не учениками, а исследователями космического пространства. А чтобы полёт прошёл удачно давайте вспомним, чем мы занимаемся на уроках математики?
Ученики: Решаем, считаем, пишем, думаем…
Учитель: А как вы думаете, что мы будем делать сегодня?
Учитель: Чтобы полёт прошёл удачно, необходимо быть:
- Внимательными
- Точно и правильно выполнять задания
- Не допускать ошибок, иначе ракета может потерпеть аварию.

В расчётное время, стартуя с Земли,
К загадочным звёздам
Летят корабли
Представим: чуть-чуть помечтали –
И все космонавтами стали.
Учитель: Итак, повышенное внимание! До старта ракеты осталось 10 секунд, давайте немного посчитаем. (Ученики ведут счёт)
- Счёт цепочкой до 10.
- Начинает учитель, дети продолжают.
- Отсчёт в обратном направлении.
- Отсчитываем секунды 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 пуск. Мы в полёте!
Учитель: Ребята, посмотрите на доску, она сегодня превратилась в «звёздное небо». Но какие необычные звёзды! Что они нам напоминают?
Ученики: геометрические фигуры.
Учитель: Что это за фигуры, назовите.
Ученики: отрезок, прямая, точки, ломаная, кривая.
Учитель: Пока мы смотрели на небо глазки устали, давайте сделаем для них зарядку.
Рисуй глазами треугольник,
Теперь его переверни
Вершиной вниз
И вновь глазами
Ты по периметру веди.
Рисуй восьмёрку вертикально
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води
И на бочок её клади.
Теперь следи горизонтально.
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы, наконец
Зарядка окончилась.
Ты молодец!
Учитель: Ребята, посмотрите, наш пульт управления находится в аварийном состоянии. Запали кнопки, необходимо исправить пульт.
- Какое число идёт при счёте за числом 3, 6, 9?
- Какое число стоит перед числом 2, 5, 8, 10?
- Назовите соседей числа 2, 7?
Но на пульте кроме цифр есть ещё различные знаки, они тоже стёрлись, давайте их восстановим (дети по очереди отвечают, остальные хлопают в ладоши, если верно)
| 2 3=5 | 4 =2 | |
| 5 1=4 | 1+ =4 | |
| 3+ =5 | 5- =4 |
Молодцы! Пульт исправен.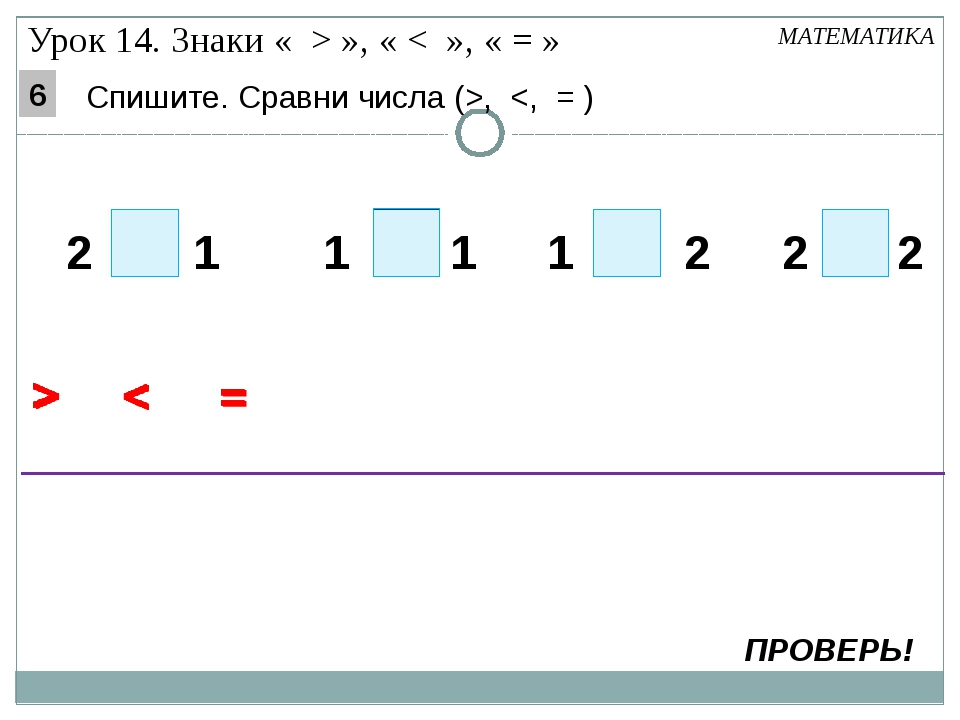
Учитель: Пока наша ракета поднимается ввысь, поиграем в игру «Сложи фигуру».
Нужно из палочек сложить фигуру, состоящую из четырёх квадратов.
Посчитай сколько здесь квадратов? (фигура состоит из 4 квадратов)
Переложи 2 палочки так, чтобы получилось 5 одинаковых квадратов.
Физминутка: (негромко звучит весёлая музыка)
На зарядку солнышко поднимает нас,
Поднимаем руки мы по команде раз,
А над нами весело шелестит листва,
Опускаем руки мы по команде два.
Соберём в корзину ягоды, грибы –
Дружно наклоняемся по команде три.
На четыре и на пять
Будем дружно мы скакать.
Ну, а по команде шесть
Всем за парты тихо сесть!
Учитель: А сейчас приготовьте свои квадраты. Положите в верхний ряд 2 зелёных квадрата, а в нижний 3 синих.
Каких квадратов меньше?
Какое число меньше 2 или 3?
В математике есть специальная запись. Это записывают так: 2
Каких квадратов больше? (синих)
Какое число больше? (3)
Кто догадался, как это записать? 3>2
> – знак больше
Знак ставится так, чтобы к большему числу «клювик» был открыт.
Давайте отдохнём и посмотрим телевизор, что у нас сегодня показывают (работа с учебником, выполнение задания).
- Сколько было птичек на первой картинке
- Сколько прилетело
- Сколько стало
- Их стало больше или меньше
- Как это записали, прочитайте
- Сколько ягод на кисточке
- Что произошло с ягодами
- Как это записать
- Какое число больше, меньше?
Учитель: Наша ракета стремительно несётся ввысь. Экипаж работает слаженно, чётко. Сейчас серьёзная работа, мы выходим в открытый космос. О, я вижу планету, от неё отделяется какой-то неожиданный летающий объект. Что это? Инопланетяне хотят уничтожить нашу ракету. Приготовьтесь к математическому сражению. А оружием будет ум и смелость. Я показываю пример, вы с помощью веера цифр ответ.
У кого можно попросить помощи, если очень трудно? (соседа по парте)
– Мы победили, корабль удаляется. Заполним ботржурналы. Проверьте рабочее место, сядьте поудобнее, чтобы бортжурналы лежали правильно, записи были чёткими и аккуратными. Работаем на странице 11. (работа в тетрадях на печатной основе для 1 класса)
Работаем на странице 11. (работа в тетрадях на печатной основе для 1 класса)
– Перед вами знаки. Как называется первый знак? (больше)
Как называется второй знак? (меньше)
Напишите знак по точкам, допишите до конца строки.
Учитель: Перед стартом ракеты я предлагаю вам поработать в паре. У вас на столах карточки, нужно вставить недостающие знаки «больше» или «меньше».
Карточка.
| 2*3 | 5*7 | 8*5 | ||
| 5*3 | 10*7 | 6*2 | ||
| 3*9 | 7*1 | 6*9 |
3. Рефлексия:
Благодаря дружной работе наша ракета совершила мягкую посадку. Во время полёта мы провели большую работу.
Во время полёта мы провели большую работу.
– Скажите, что вы для себя узнали нового?
– Чем мы сегодня занимались?
– Что вам помогло хорошо работать на уроке?
У вас на столах лежат мордочки, нарисуйте на них выражения лица весёлое или грустное, кому на уроке было хорошо поднимите весёлую мордочку. А у кого что-то не получилось и было грустно? (таких может не быть)
Полёт завершён, всем спасибо!
Горячие клавиши занимают важное место среди способов, позволяющих ускорить взаимодействие с компьютером. Благодаря ним, мы получаем доступ к нужной функции почти мгновенно, вместо долгого блуждания по пунктам меню и попадания в них мышкой. Поэтому горячие клавиши одинаково полезны как новичкам, так и опытным пользователям. На страницах МакРадара, мы уже неоднократно поднимали тему горячих клавиш. В этой статье я расскажу о клавишах-модификаторах, которые охватывают различные области применения и о прямом вводе популярных спецсимволов.
Примечание . Что качается ввода спецсимволов, то некоторые из них нужно вводить в английской раскладке, поскольку в русской — там будут находится совсем другие символы.
Что качается ввода спецсимволов, то некоторые из них нужно вводить в английской раскладке, поскольку в русской — там будут находится совсем другие символы.
Математические символы
Для учеников, студентов, научных работников и вообще всех тех, кому приходится часто возится с уравнениями и математическими символами на своих Mac’ах — очень полезно будет знать как вводить их напрямую с клавиатуры, не прибегая к банку символов или заменяя их похожими (вроде м3 или
1. Знак неравенства ≠
Чтобы вставить математический символ ≠ жмем ⌥ = .
2. Знак плюс-минус ±
Для ввода знака ± — жмем ⇧⌥ = (англ. раскладка) или ⇧ ⌥§ (русская).
3. Знак бесконечности ∞
Если вам нужно поставить символ ∞ — жмем ⌥ 5 (англ. раскладка).
4. Многоточие …
Чтобы вставить многоточие, не нужно ставить три точки — просто нажмите ⌥ ; (англ. раскладка).
5. Знак деления ÷
Чтобы получить этот символ ÷ — жмем ⌥ / (англ. раскладка).
6. Знак «больше или равно» ≥
Для вставки символа «больше или равно» нужно нажать ⌥ > .
7. Знак «меньше или равно» ≤
Чтобы получить противоположный символ ≤ — жмем ⌥ .
8. Знак Пи π
Часто в уравнениях и расетах встречается число π, если вам нужно его ввести — жмем ⌥ P (англ. раскладка).
Работа со скриншотами
9. Скриншот всего экрана
Чтобы сделать снимок всего экрана — жмем ⌘ ⇧ 3 . Скриншот автоматически сохранится на рабочий стол.
10. Скриншот области экрана
В этом случае жмем ⌘ ⇧ 4 и не отпуская клавиш выделяем нужную область экрана.
11. Скриншот определенного окна
Иногда нужно сделать скриншот отдельного окна, для этого жмем ⌘ ⇧ 4 потом Пробел и делаем клик.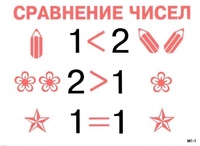 (после нажатия пробела можно перемещаться между окнами для выбора нужного).
(после нажатия пробела можно перемещаться между окнами для выбора нужного).
12. Копирование скриншота в буфер обмена
Автоматически все скриншоты сохраняются на рабочий стол, но если вы трепетно относитесь к порядку на нем и не допускаете захламления — просто добавьте к приведенным выше комбминациям клавишу ⌃ . То есть, ⌘ ⇧ 4⌃ сделает скриншот выбранного окна и скопирует его в буфер обмена.
Ввод спецсимволов
С помощью клавиатуры можно вводить не только символы нанесенные на клавишах, но много других полезных символов привязанных к конкретной клавише. Вот несколько популярных символов, которые могут вам пригодится.
13. Trademark ™
Если нужно ввести значок ™ торговая марка — жмем ⌥ 2 .
14. Registered Trademark ®
Для ввода зарегистрированного товарного знака — жмем ⌥ R .
15. Копирайты ©
Жмем ⌥ G, чтобы получить символ копирайта.
16. Символ валюты евро €
Для ввода символа евро жмем ⌥⇧ 2 .
17. Элемент маркированного списка
Быстро создать аккуратный маркированный список можно нажав ⌥ 8 на каждой его строчке.
18. Символ параграфа ¶
Если вам нужно указать символ параграфа нажимаем ⌥ 7.
19. Даггер (символ сноски) †
Нажимаем ⌥ Т для вставки символа обозначающего сноску.
20. Градус º
Жмем ⌥ 0 для ввода градуса.
21. Греческие буквы дельта, бета и омега ∂ ß Ω
Если понадобится ввести буквы греческого алфавита ∂ , ß , Ω — жмем ⌥ D , ⌥ S , ⌥ Z , соответственно.
Загрузка системы, выключение
Во время загрузки Mac’а можно использовать различные клавиши для определенного типа загрузки. Вот некоторые из них.
22. Показ загрузочных дисков
Удерживая ⌥ во время загрузки можно отобразить все доступные загрузочные диски.
23. Загрузка в безопасном режиме
Для загрузки в безопасном режиме удерживаем клавишу ⇧ .
24. Загрузка с внешнего диска
Иногда бывает необходимо загрузиться с внешнего источника: USB, DVD – для этого удерживаем клавишу С .
25. Режим восстановления (recovery)
Для загрузки в режиме восстановления следует удерживать комбинацию ⌘ R .
26. Загрузка в режиме Single User Mode
Жмем ⌘ S для того, чтобы загрузиться в этом режиме.
27. Переход в спящий режим
При нажатии ⌘⌥⏏ ваш Mac перейдет в режим сна.
28. Вызов меню выключения/перезагрузки
Нажатие ⌃ ⏏ откроет стандартный диалог выключение/перезагрузка/спящий режим.
Горячие клавиши для Корзины
Удаление файлов можно выполнять разными путями, но проще всего это делать с помощью шорткатов. Также есть комбинации для очистки и полной очистки Корзины. О них далее.
О них далее.
29. Удаление файлов
Для удаления выбранных файлов нужно нажать ⌘⌫ . На больших клавиатурах, где есть клавиша ⌦ , можно жать ⌘⌦ .
30. Восстановление файлов
Чтобы восстановить выбранные файлы из Корзины нужно нажать ту же комбинацию ⌘⌫ (⌘⌦ ).
31. Очистка Корзины
Для очистки Корзины жмем ⌘ ⇧ ⌫ в Finder. После этого нужно подтвердить удаление.
32. Очистка Корзины (без подтверждения)
Чтобы очистить Корзину без запроса подтверждения удаления нужно нажать ⌘⌥ ⇧ ⌫ (⌘⌥ ⇧ ⌦ ).
33. Бонус
Для вставки логотипа компании Apple используем шорткат ⌥ ⇧ K .
Если вам понравилось работать с горячими клавишами, рекмендую ознакомиться с предыдущими подборками, которые публиковались на МакРадаре.
- 50+ полезных горячих клавиш для продуктивной работы в Safari
Как всегда, приветствуются ваши комментарии, уважаемые читатели. Расскажите о своих любимых шорткатах — мы всегда рады услышать ваше мнение!
Расскажите о своих любимых шорткатах — мы всегда рады услышать ваше мнение!
§ Как решать линейные неравенства
Прежде чем перейти к определению и решению неравенств давайте вспомним, какие знаки используют в математике для сравнения величин.
Теперь мы можем разобраться, что называют линейным неравенством и чем неравенство отличается от уравнения.
В отличии от уравнения в неравенстве вместо знака равно «=» используют любой знак сравнения: «>», «», «≤» или «≥».
Рассмотрим пример линейного неравенства.
x − 6Так как в неравенстве «x − 6 » неизвестное «x» стоит в первой степени, такое неравенство называют линейным.
Как решить линейное неравенство
Важно!Чтобы решить неравенство, нужно чтобы в левой части осталось только неизвестное в первой степени с коэффициентом «1».
При решении линейных неравенств используют правило переноса и правило деления неравенства на число.
Правило переноса в неравенствах
Также как и в уравнениях, в неравенствах можно переносить любой член неравенства из левой части в правую и наоборот.
Запомните!При переносе из левой части в правую (и наоборот) член неравенства меняет свой знак на противоположный.
Вернемся к нашему неравенству и используем правило переноса.
x − 6
x + 6
x
Итак, мы получили ответ к неравенству «x ». Но что означает такой ответ?
Для того, чтобы понять, что получается при решении неравенства, нам нужно вспомнить, понятие числовой оси.
Нарисуем числовую ось для неизвестного «x» и отметим на ней число «14».
Запомните!При нанесении числа на числовую ось соблюдаются следующие правила:
- если неравенство строгое, то число отмечается как «пустая» точка.
Это означает, что число не входит в область решения;
- если неравенство нестрогое, то число отмечается как «заполненная» точка.
 Это означает, что число входит в область решения.
Это означает, что число входит в область решения.
Заштрихуем на числовой оси по полученному ответу «x » все решения неравенства, то есть область слева от числа «14».
Рисунок выше говорит о том, что любое число из заштрихованной области при подстановке в исходное неравенство «x − 6 » даст верный результат.
Возьмем, например число «12» из заштрихованной области и подставим его вместо «x» в исходное неравенство «x − 6 ».
12 − 6 6 (верно)Другими словами, можно утверждать, что любое число из заштрихованной области будет являться решением неравенства.
Важно!Решить неравенство — это значит найти множество чисел, которые при подстановке в исходное неравенство дают верный результат.
Решением неравенства
называют множество чисел из заштрихованной области на числовой оси.
В нашем примере ответ «x » можно понимать так: любое число из заштрихованной области (то есть любое число меньшее «14») будет являться решением неравенства «x − 6 ».
Правило умножения или деления неравенства на число
Рассмотрим другое неравенство.
2x − 16 > 0
Используем правило переноса и перенесём все числа без неизвестного, в правую часть.
2x − 16 > 0
2x > 16
Теперь нам нужно сделать так, чтобы при неизвестном «x» стоял коэффициент «1». Для этого достаточно разделить и левую, и правую часть на число «2».
Запомните!При умножении или делении неравенства на число, на это число умножается (делится) и левая, и правая часть.
- Если неравенство умножается (делится) на положительное число,
то
знак самого неравенства остаётся прежним. - Если неравенство умножается (делится) на отрицательное число,
то
знак самого неравенства меняется на противоположный.
Разделим «2x > 16» на «2». Так как «2» — положительное число, знак неравенства останется прежним.
2x > 16 | (:2)2x (:2) > 16 (:2)
x > 8
Ответ: x > 8
Рассмотрим другое неравенство.
9 − 3x ≥ 0
Используем правило переноса.
9 − 3x ≥ 0
−3x ≥ −9
Разделим неравенство на «−3». Так как мы делим неравенство на отрицательное число, знак неравенства поменяется на противоположный.
−3x ≥ −9−3x ≥ −9 | :(−3)
−3x : (−3) ≤ −9 :(−3)
x ≤ 3
Ответ: x ≤ 3
Примеры решения линейных неравенств
- 4(x − 1) ≥ 5 + x
4x − 4 ≥ 5 + x
4x − x ≥ 5 + 4
3x ≥ 9 | (:3)
3x (:3) ≥ 9 (:3)
x ≥ 3
Ответ: x ≥ 3 - x + 2
x + 2
x − 3x
−2x
−2x 0 | :(−2)
−2x : (−2) > 0 : (−2)
x > 0
Ответ: x > 0
Метод интервалов (ЕГЭ 2022) | ЮКлэва
Что такое интервал?
Это некий промежуток числовой прямой, то есть все возможные числа, заключенные между двумя какими-то числами – концами интервала. Эти промежутки в голове представить не так просто, поэтому интервалы принято рисовать, сейчас научу.
Эти промежутки в голове представить не так просто, поэтому интервалы принято рисовать, сейчас научу.
Рисуем ось \( X\), на ней располагается весь числовой ряд от \( -\infty \) и до \( +\infty \). На ось наносятся точки, те самые так называемые нули функции, значения, при которых выражение равняется нулю.
Эти точки «выкалываются» что означает, что они не относятся к числу тех значений, при которых неравенство верно. В данном случае, они выкалываются, т.к. знак в неравенстве \( >\), а не \(\ge\), то есть строго больше, а не больше или равно.
Хочу сказать, что ноль отмечать не обязательно, он без кружочков тут, а так, для понимания и ориентации по оси.
Ладно, ось нарисовали, точки (точнее кружочки) поставили, дальше что, как мне это поможет в решении? – спросишь ты.
Теперь просто…
Возьми значение для икса из интервалов по порядку и подставь их в свое неравенство и смотри, какой знак будет в результате умножения.
Короче, просто берем \( -2\) например, подставляем его сюда \( (x+1)\cdot ({x}-2)\), получится \( 4\), а \( 4>0\).
Значит на всем промежутке (на всем интервале) от \( -\infty \) до \( -1\), из которого мы брали \( -2\), неравенство будет справедливо.
Иными словами если икс от \( -\infty \) до \( -1\), то неравенство верно.
То же самое делаем и с интервалом от \( -1\) до \( 2\), берем \( 0\) или \( 1\), например, подставляем в \( (x+1)\cdot ({x}-2)\), определяем знак, знак будет «минус». И так же делаем с последим, третьим интервалом от \( 2\) до \( +\infty \), где знак получится «плюс».
Такая куча текста вышла, а наглядности мало, правда?
Взгляни еще раз на неравенство \( (x+1)\cdot ({x}-2)>0\).
Теперь все на ту же ось наносим еще и знаки, которые получатся в результате. Ломаной линией в моем примере обозначаем положительные и отрицательные участки оси.
Смотри на неравенство – на рисунок, опять на неравенство – и снова на рисунок, что-нибудь понятно?
Постарайся теперь сказать на каких промежутках икса, неравенство будет верно.
Правильно, от \( -\infty \) до \( -1\) неравенство будет справедливо и от \( 2\) до \( +\infty \).
А на промежутке от \( -1\) до \( 2\) неравенство \( <\) нуля и нас этот промежуток мало интересует, ведь у нас в неравенстве знак \( >\) стоит.
Ну, раз ты с этим разобрался, то дело за малым – записать ответ!
В ответ пишем те промежутки, при которых левая часть больше нуля, \( x\in (-\infty ;-1)\cup (2;+\infty )\), что читается, как икс принадлежит промежутку от минус бесконечности до минус одного и от двух до плюс бесконечности.
Стоит пояснить, что круглые скобки означают, что значения, которыми ограничен интервал не являются решениями неравенства, то есть они не включены в ответ, а лишь говорят о том, что до \( -1\), например, но \( -1\) не есть решение.
Теперь пример, в котором тебе придется не только интервал рисовать.
занятие по фэмп в старшей группе. больше, меньше. | План-конспект занятия по математике (старшая группа) на тему:
Занятие по ФЭМП в старшей группе
«Больше.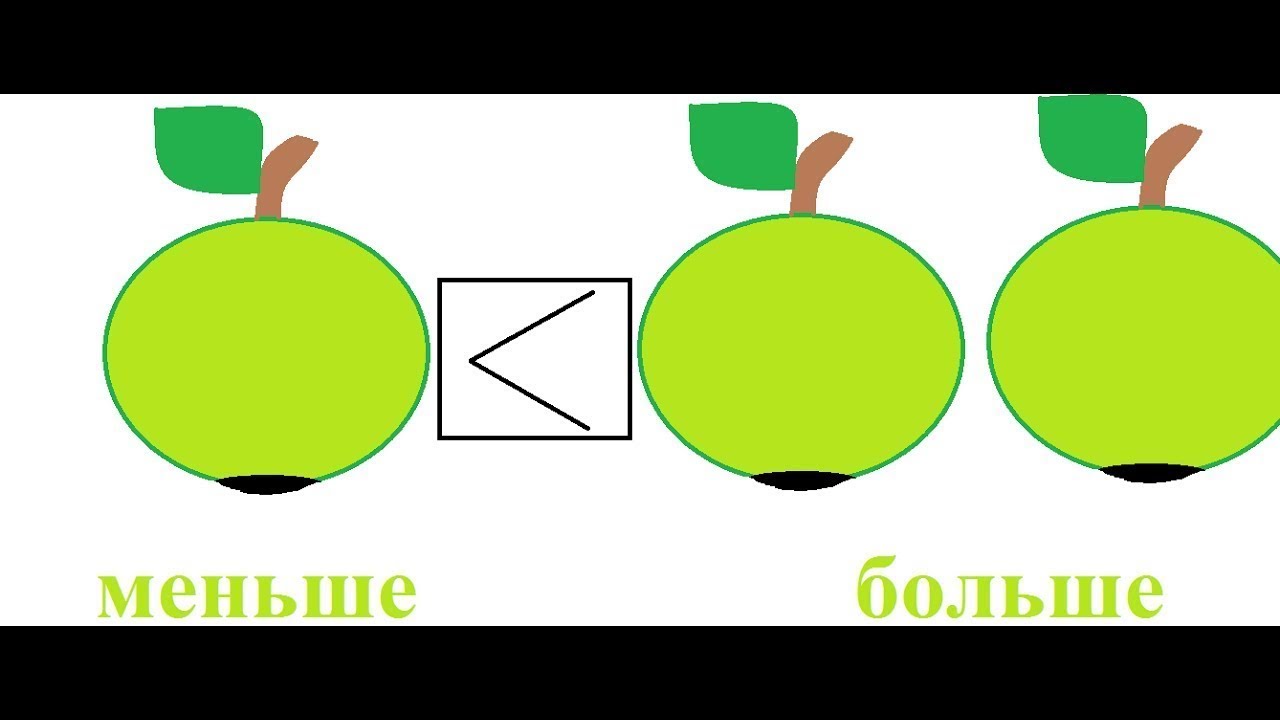 Меньше. Знаки »
Меньше. Знаки »
Выполнила воспитатель
Тютикова Евгения Маргалимовна
Цель: закрепить сравнение групп предметов по количеству с помощью составления пар. Познакомить со знаками .
Материалы к занятию:
Демонстрационный – 5 одинаковых котят с разноцветными бантиками; 5 клубков разноцветных, под цвет бантиков; карточки с цифрами от 1 до 5; две полоски бумаги – модели знаков равенства и неравенства.
Раздаточный – счетные палочки; карточки с цифрами от 1 до 5.
Ход занятия:
- Формирование представлений об отношениях больше, меньше. Знакомство со знаками .
В. – Ребята, давайте встанем в круг и попробуем отгадать загадку про наших гостей.
Он пушистый, он игривый,
Очень-очень шаловливый,
Часто любит хвост ловить,
Молоко парное пить.
Испугаешь – он шипит,
Спинку выгибает,
Приласкаешь – он мурчит,
Весело играет.
(Котенок)
Д. – Котенок.
В. – Молодцы. Присаживайтесь. Сегодня к нам в гости пришли котята (котята выставлены на магнитной доске). Посмотрите, какие они пушистые, нежные… Они все одинаковые, а бантики у них разных цветов. Котята очень любят играть с клубками (рядом с каждым котенком стоит клубочек по цвету бантика). Как вы думаете, у каждого котенка есть свой клубок? Как нам это узнать?
Присаживайтесь. Сегодня к нам в гости пришли котята (котята выставлены на магнитной доске). Посмотрите, какие они пушистые, нежные… Они все одинаковые, а бантики у них разных цветов. Котята очень любят играть с клубками (рядом с каждым котенком стоит клубочек по цвету бантика). Как вы думаете, у каждого котенка есть свой клубок? Как нам это узнать?
Д. – Сравнить количество котят и количество клубков.
В. – Правильно. А как вы будете сравнивать?
Д. – Мы посчитаем котят и клубочки. И сравним (если заметят, то скажут, что у каждого котенка есть пара – клубочек по цвету). Котят и клубочков по 5. Значит их поровну.
Ребята считают и делают вывод, что котят и клубочков поровну.
Можно спросить их, какой способ решения проще и почему.
В. – Ребята, положите у себя на листке справа и слева по цифре 5. И поставьте, с помощью счетных палочек, знак равенства.
Затем на доске выставляю две цифры 5 и знак равенства между ними моделирую из 2 полосок.
В. – Молодцы. Правильно посчитали. И котят и клубков поровну. Но вот несколько котят убежали за своими клубочками в сторону (ставлю трех котят с клубками в левую сторону доски, а двух котят, с их клубками, в правую сторону доски). Сколько стало котят справа доски?
Д. – Двое котят.
В. – Правильно. А сколько котят осталось слева?
Д. – Трое котят.
В. – Хорошо. Но тут прилетела птичка и открыла клюв от удивления. Какие красивые котята. Посмотрите на ее клюв – в какую сторону он открыт?
Д. – Птичка открыла клюв в ту сторону, где котят больше. Их трое.
Давайте положим слева цифру 3, а справа цифру 2. Выкладываю на доске цифры 3 и 2 и между ними две полоски, моделирующие знак равенства.
В. – Посмотрите, правильно ли я поставила знак равенства?
Д. – Нет.
В. – Почему? (потому что 3 больше 2). Как превратить полоски в раскрытый клюв птички?
«Раскрываю» полоски в сторону числа три и получаю знак >. Дети делают то же на столах из счетных палочек.
В. – Посмотрите, получается, что три больше двух. Это показывает знак «больше». А сейчас 2 котенка справа перебежали к двум котятам справа. Что произошло?
Д. – Слева остался один котенок, а справа стало четыре котенка.
В. – Давайте положим слева цифру 1, а справа цифру 4. Как вы думаете, как теперь надо положить полоски?
Д. – Так, чтобы клюв открылся на цифру 4.
В. – Что теперь получилось?
Д. – 1 меньше четырех.
В. – Посмотрите, ребята, клюв птички всегда показывает на то число, которое меньше. Ну что устали? Давайте отдохнем.
2. Физминутка «Мы считали, мы считали…»
Мы считали, мы считали,
А теперь тихонько встали.
Раз – присели, два – нагнулись,
На носочках потянулись.
Руки ставим на бочок:
На носочках скок, скок, скок.
3.Закрепление представлений о сравнении групп предметов с помощью знаков . (Совместная работа по тетрадям).
4. Итог занятия.
— Понравилось вам занятие? Кому мы помогали? Какие математические знаки мы узнали? (больше, меньше) Куда смотрит носик этих знаков? (всегда на меньшее число). Все вы сегодня были молодцы, помогли котятам найти свои клубочки. Они вам благодарны.
Логические выражения и операторы. Курс «Python. Введение в программирование»
Логические выражения и логический тип данных
Часто в реальной жизни мы соглашаемся с каким-либо утверждением или отрицаем его. Например, если вам скажут, что сумма чисел 3 и 5 больше 7, вы согласитесь, скажете: «Да, это правда». Если же кто-то будет утверждать, что сумма трех и пяти меньше семи, то вы расцените такое утверждение как ложное.
Подобные фразы предполагают только два возможных ответа – либо «да», когда выражение оценивается как правда, истина, либо «нет», когда утверждение оценивается как ошибочное, ложное. В программировании и математике если результатом вычисления выражения может быть лишь истина или ложь, то такое выражение называется логическим.
Например, выражение 4 > 5 является логическим, так как его результатом является либо правда, либо ложь. Выражение 4 + 5 не является логическим, так как результатом его выполнения является число.
На позапрошлом уроке мы познакомились с тремя типами данных – целыми и вещественными числами, а также строками. Сегодня введем четвертый – логический тип данных (тип bool). Его также называют булевым. У этого типа всего два возможных значения: True (правда) и False (ложь).
>>> a = True >>> type(a) <class 'bool'> >>> b = False >>> type(b) <class 'bool'>
Здесь переменной a было присвоено значение True, после чего с помощью встроенной в Python функции type() проверен ее тип. Интерпретатор сообщил, что это переменная класса bool. Понятия «класс» и «тип данных» в данном случае одно и то же. Переменная b также связана с булевым значением.
В программировании False обычно приравнивают к нулю, а True – к единице. Чтобы в этом убедиться, можно преобразовать булево значение к целочисленному типу:
>>> int(True) 1 >>> int(False) 0
Возможно и обратное. Можно преобразовать какое-либо значение к булевому типу:
>>> bool(3.4)
True
>>> bool(-150)
True
>>> bool(0)
False
>>> bool(' ')
True
>>> bool('')
FalseИ здесь работает правило: всё, что не 0 и не пустота, является правдой.
Логические операторы
Говоря на естественном языке (например, русском) мы обозначаем сравнения словами «равно», «больше», «меньше». В языках программирования используются специальные знаки, подобные тем, которые используются в математике: > (больше), < (меньше), >= (больше или равно), <= (меньше или равно), == (равно), != (не равно).
Не путайте операцию присваивания значения переменной, обозначаемую в языке Python одиночным знаком «равно», и операцию сравнения (два знака «равно»). Присваивание и сравнение – разные операции.
>>> a = 10 >>> b = 5 >>> a + b > 14 True >>> a < 14 - b False >>> a <= b + 5 True >>> a != b True >>> a == b False >>> c = a == b >>> a, b, c (10, 5, False)
В данном примере выражение c = a == b состоит из двух подвыражений. Сначала происходит сравнение (==) переменных a и b. После этого результат логической операции присваивается переменной c. Выражение a, b, c просто выводит значения переменных на экран.
Сложные логические выражения
Логические выражения типа kByte >= 1023 являются простыми, так как в них выполняется только одна логическая операция. Однако, на практике нередко возникает необходимость в более сложных выражениях. Может понадобиться получить ответа «Да» или «Нет» в зависимости от результата выполнения двух простых выражений. Например, «на улице идет снег или дождь», «переменная news больше 12 и меньше 20″.
В таких случаях используются специальные операторы, объединяющие два и более простых логических выражения. Широко используются два оператора – так называемые логические И (and) и ИЛИ (or).
Чтобы получить True при использовании оператора and, необходимо, чтобы результаты обоих простых выражений, которые связывает данный оператор, были истинными. Если хотя бы в одном случае результатом будет False, то и все сложное выражение будет ложным.
Чтобы получить True при использовании оператора or, необходимо, чтобы результат хотя бы одного простого выражения, входящего в состав сложного, был истинным. В случае оператора or сложное выражение становится ложным лишь тогда, когда ложны оба составляющие его простые выражения.
Допустим, переменной x было присвоено значение 8 (x = 8), переменной y присвоили 13 (y = 13). Логическое выражение y < 15 and x > 8 будет выполняться следующим образом. Сначала выполнится выражение y < 15. Его результатом будет True. Затем выполнится выражение x > 8. Его результатом будет False. Далее выражение сведется к True and False, что вернет False.
>>> x = 8 >>> y = 13 >>> y < 15 and x > 8 False
Если бы мы записали выражение так: x > 8 and y < 15, то оно также вернуло бы False. Однако сравнение y < 15 не выполнялось бы интерпретатором, так как его незачем выполнять. Ведь первое простое логическое выражение (x > 8) уже вернуло ложь, которая, в случае оператора and, превращает все выражение в ложь.
В случае с оператором or второе простое выражение проверяется, если первое вернуло ложь, и не проверяется, если уже первое вернуло истину. Так как для истинности всего выражения достаточно единственного True, неважно по какую сторону от or оно стоит.
В языке Python есть еще унарный логический оператор not, то есть отрицание. Он превращает правду в ложь, а ложь в правду. Унарный он потому, что применяется к одному выражению, стоящему после него, а не справа и слева от него как в случае бинарных and и or.
Здесь у < 15 возвращает True. Отрицая это, мы получаем False.
>>> a = 5 >>> b = 0 >>> not a False >>> not b True
Число 5 трактуется как истина, отрицание истины дает ложь. Ноль приравнивается к False. Отрицание False дает True.
Практическая работа
Присвойте двум переменным любые числовые значения.
Используя переменные из п. 1, с помощью оператора
andсоставьте два сложных логических выражения, одно из которых дает истину, другое – ложь.Аналогично выполните п. 2, но уже с оператором
or.Попробуйте использовать в логических выражениях переменные строкового типа. Объясните результат.
Напишите программу, которая запрашивала бы у пользователя два числа и выводила бы
TrueилиFalseв зависимости от того, больше первое число второго или нет.
Примеры решения и дополнительные уроки в android-приложении и pdf-версии курса
Как пишется знак больше и знак меньше
Как и в какую сторону пишется знак больше
В общем и целом логика понимания очень проста – какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону – такой и знак. Соответственно, знак больше влево смотрит широкой стороной – большей.
Пример использования знака больше:
- 50>10 – число 50 больше числа 10;
- посещаемость студента в этом семестре составила >90% занятий.
Как пишется знак больше и знак меньше
Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как знак больше и знак меньше, а также знак равно.
Однако, если с последним что-то напутать достаточно сложно, то о том, как и в какую сторону пишутся знаки больше и меньше (знак менее и знак более, как ещё их иногда называют) многие сразу после этой же школьной скамьи и забывают, т.к. они довольно редко используются нами в повседневной жизни.
Но практически каждому рано или поздно всё равно приходится столкнуться с ними, и «вспомнить» в какую сторону пишется нужный им символ получается лишь обратившись за помощью к любимой поисковой системе. Так почему бы не ответить развернуто на этот вопрос, заодно подсказав посетителям нашего сайта как запомнить правильное написание этих знаков на будущее?
Именно о том, как правильно пишется знак больше и знак меньше мы и хотим напомнить вам в этой небольшой заметке. Также будет не лишним рассказать и том, как набрать на клавиатуре знаки больше или равно и меньше или равно, т.к. этот вопрос тоже довольно часто вызывает затруднения у пользователей, сталкивающихся с такой задачей очень редко.
Перейдем сразу к делу. Если вам не очень интересно запоминать всё это на будущее и проще в следующий раз снова «погуглить», а сейчас просто нужен ответ на вопрос «в какую сторону писать знак», тогда для вас мы приготовили краткий ответ — знаки больше и меньше пишутся так, как показано на изображении ниже.
А теперь расскажем немного подробнее о том, как это понять и запомнить на будущее.
Детская игра “Больше-меньше” – развивающие игры на логику
ангелина | 15/01/2017 19:31
игра совсем для малышей
мадина | 09/08/2016 06:37
мне 4годимка игры для малышей это самая крутая вещь
оля и катя | 14/12/2015 18:41
а я с сестрой не одной ошибки не зделала и нам за это МОЛОДЕЦ!!!!!!!!! я ваще от нее во сторге!
вера | 20/10/2015 19:57
мне 3 года и я выиграла! мне игра нравится
Эмиль | 04/07/2015 23:52
Но как все так быстро передвигается?
ариша 12 лет | 08/02/2015 15:51
мне очень нравится музыка в этой игре прям плаачу)))))
Настя | 05/11/2014 11:42
я в 5 играю с племяшкой и меня удивляет что тут делает 4 и 3 класс
оля | 27/03/2014 08:04
СОВСЕМ ДЛЯ МАЛЕНЬКИХ
софья | 25/03/2014 09:04
нормально
Areg Gevorgyan | 16/09/2013 13:17
игра просто супер класс
геля | 19/07/2013 15:23
я в 4 классе , прошла за считанные секунды!
Катя Понкаратова | 01/11/2012 17:14
я в 2 классе и игра мне нравится
линда | 09/10/2012 18:28
я хожу в (3 клас) и мне ета игра нравитса!!!!!!!!!!!!!!!!!!!!=))
кристина | 28/09/2012 17:37
так себе
марина | 08/06/2012 14:18
игра очень хорошая
Аня и Миша | 06/06/2012 16:40
Прошла я замечательно!
глеб | 31/05/2012 19:21
3 года хорошие игры
Марина | 10/05/2012 11:44
я в 4 классе игра класссс!!!!! я от нее в восторге!!!
Катя | 04/05/2012 16:00
для 1 класса (я 3 заканчиваю)
даша | 03/05/2012 11:18
интересная игра
арина | 02/05/2012 21:28
отлично
Ирина | 20/04/2012 22:13
Моей дочке 3 года мы прошли эту игру за 4 минуты и у неё 2 ошибки
МИША | 19/04/2012 21:16
МНЕ 5 ЛЕТ МНЕ ОЧЕНЬ ПОНРАВИЛАСЬ ЭТА ИГРА…Я ИГРАЛ С МАМОЙ….
оля | 01/04/2012 18:57
очень красивая игра
Настя. | 30/03/2012 23:47
очень хорошая игра.Мне 6-лет.
Саманта 8 лет | 24/03/2012 15:34
за 3 сек а ошибки 2
настя | 23/03/2012 08:24
мне 5 лет я прошла без ошибок,! ладно шутка!, мне11 лет, так зашла делать нечего, я в 4 классе
Катерина | 15/03/2012 19:15
Дана, если тебе не нравятся такие игры и ты считаеншь что они для маленьких, так не играй в них!мы тут развиваем своё мышление и мышление наших младших братьев и сестер
хХMaschaBestХх | 27/02/2012 22:23
Я согласна с Анной! И про Дану какое отношение к игре имеет в каком ты классе?!Это ни кому не интересно!….
ДАНА | 06/02/2012 20:39
МНЕ 7,5 ЛЕТ Я СТАРАСТА КЛАССА Я В 1 КЛАССЕ
Влад (7лет) | 19/02/2012 19:46
я тоже в 1 классе.
ДАНА | 06/02/2012 20:36
Я ДУМАЮ ШТО ЭТА ИГРА МАЛЕНЬКИХ!!
Анна | 21/02/2012 23:23
Знаешь,ты сейчас тоже маленькая.Все мы маленькие.И “што” пишется что.И ещё на конец скажу,даже такие простые задание на маленький шажок продвигает тебя к великим знаниям.(я даже не про игру,я говорю про всё)
ирина | 30/01/2012 15:32
игра просто супер класс
Лена | 28/01/2012 19:56
моей дочке 4года для неё игра эта легкая. Я думаю она расчитана на возраст 2-3года.
Ксюша | 04/01/2012 19:17
Клас!!!!!!!!!!Я Ксюша всем привет
Настя | 25/12/2011 11:42
игра конеччно очень очень лёгкая! мне 10
дженнет | 06/12/2011 13:27
это хорошая игра! Всем привет как ваши дела?
Меня зовут Дженнет мне 13 лет
Алина | 04/12/2011 16:14
нормально!!!!!
Вил | 01/12/2011 15:19
Моей сестре 6 лет…. она отлично справляется=)
www.igraemsa.ru
Как пишется знак больше и знак меньше
Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как знак больше и знак меньше, а также знак равно.
Однако, если с последним что-то напутать достаточно сложно, то о том, как и в какую сторону пишутся знаки больше и меньше (знак менее и знак более, как ещё их иногда называют) многие сразу после этой же школьной скамьи и забывают, т.к. они довольно редко используются нами в повседневной жизни.
Но практически каждому рано или поздно всё равно приходится столкнуться с ними, и «вспомнить» в какую сторону пишется нужный им символ получается лишь обратившись за помощью к любимой поисковой системе. Так почему бы не ответить развернуто на этот вопрос, заодно подсказав посетителям нашего сайта как запомнить правильное написание этих знаков на будущее?
Именно о том, как правильно пишется знак больше и знак меньше мы и хотим напомнить вам в этой небольшой заметке. Также будет не лишним рассказать и том, как набрать на клавиатуре знаки больше или равно и меньше или равно, т.к. этот вопрос тоже довольно часто вызывает затруднения у пользователей, сталкивающихся с такой задачей очень редко.
Содержание:
- Как пишется знак больше
- Как пишется знак меньше
- Знак «больше или равно»/«меньше или равно» (как набрать на клавиатуре)
Перейдем сразу к делу. Если вам не очень интересно запоминать всё это на будущее и проще в следующий раз снова «погуглить», а сейчас просто нужен ответ на вопрос «в какую сторону писать знак», тогда для вас мы приготовили краткий ответ — знаки больше и меньше пишутся так, как показано на изображении ниже.
А теперь расскажем немного подробнее о том, как это понять и запомнить на будущее.
Как и в какую сторону пишется знак больше
В общем и целом логика понимания очень проста — какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону — такой и знак. Соответственно, знак больше влево смотрит широкой стороной — большей.
Пример использования знака больше:
- 50>10 — число 50 больше числа 10;
- посещаемость студента в этом семестре составила >90% занятий.
Как и в какую сторону пишется знак меньше
Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной — меньшей, то перед вами знак меньше.
Пример использования знака меньше:
- 100<500 — число 100 меньше числа пятьсот;
- на заседание явилось <50% депутатов.
Как видите, все довольно логично и просто, так что теперь вопросов о том, в какую сторону писать знак больше и знак меньше в будущем у вас возникать не должно.
Знак больше или равно/меньше или равно
Если вы уже вспомнили, как пишется необходимый вам знак, то дописать к нему одну черточку снизу вам не составит труда, таким образом вы получите знак «меньше или равно» или знак «больше или равно».
Однако относительно этих знаков у некоторых возникает другой вопрос — как набрать такой значок на клавиатуре компьютера? В результате большинство просто ставят два знака подряд, к примеру, «больше или равно» обозначая как «>=», что, в принципе, часто вполне допустимо, но можно сделать красивее и правильнее.
На самом деле для того, чтобы напечатать эти знаки, существуют специальные символы, которые можно ввести на любой клавиатуре. Согласитесь, знаки «≤» и «≥» выглядят значительно лучше.
Знак больше или равно на клавиатуре
Для того, чтобы написать «больше или равно» на клавиатуре одним знаком даже не нужно лезть в таблицу специальных символов — просто поставьте знак больше с зажатой клавишей «alt». Таким образом сочетание клавиш (вводится в английской раскладке) будет следующим.
alt+ю
Или же вы можете просто скопировать значок из этой статьи, если вам нужно воспользоваться им один раз. Вот он, пожалуйста.
≥
Знак меньше или равно на клавиатуре
Как вы наверное уже смогли догадаться сами, написать «меньше или равно» на клавиатуре вы можете по аналогии со знаком больше — просто поставьте знак меньше с зажатой клавишей «alt». Сочетание клавиш, которое нужно вводить в английской раскладке, будет следующим.
alt+б
Или просто скопируйте его с этой страницы, если вам так будет проще, вот он.
≤
Как видите, правило написания знаков больше и меньше довольно просто запомнить, а для того чтобы набрать значки больше или равно и меньше или равно на клавиатуре достаточно просто нажать дополнительную клавишу — всё просто.
© OchProsto.com
ochprosto.com
Приблизительно равные числа. Обозначения и символика
Балагин Виктор
С открытием математических правил и теорем ученые придумывали новые математические обозначения, знаки. Математические знаки — это условные обозначения, предназначенные для записи математических понятий, предложений и выкладок. В математике употребляются специальные символы, позволяющие сократить запись и точнее выразить утверждение. Помимо цифр и букв различных алфавитов (латинского, греческого, еврейского) математический язык используют множество специальных символов, изобретенных за последние несколько столетий.
Скачать:
Предварительный просмотр:
МАТЕМАТИЧЕСКИЕ СИМВОЛЫ.
Работу выполнил
Ученик 7-а класса
ГБОУ СОШ № 574
Балагин Виктор
2012-2013 уч.год
МАТЕМАТИЧЕСКИЕ СИМВОЛЫ.
- Введение
Слово математика пришло к нам из древнегреческого, где μάθημα означало «учиться», «приобретать знания». И не прав тот, кто говорит: «Мне не нужна математика, я ведь не собираюсь стать математиком». Математика нужна всем. Раскрывая удивительный мир окружающих нас чисел, она учит мыслить яснее и последовательнее, развивает мысль, внимание, воспитывает настойчивость и волю. М.В.Ломоносов говорил: «Математика ум в порядок приводит». Одним словом, математика учит нас учиться приобретать знания.
Математика – это первая наука, которую смог освоить человек. Самой древней деятельностью был счёт. Некоторые первобытные племена подсчитывали количество предметов с помощью пальцев рук и ног. Наскальный рисунок, сохранившийся, до наших времён от каменного века изображает число 35 в виде нарисованных в ряд 35 палочек. Можно сказать, что 1 палочка – это первый математический символ.
Математическая «письменность», которую мы сейчас используем — от обозначений неизвестных буквами x, y, z до знака интеграла — складывалась постепенно. Развитие символики упрощало работу с математическими операциями и способствовало развитию самой математики.
С древнегреческого «символ» (греч. symbolon – признак, примета, пароль, эмблема) – знак, который связан с обозначаемой им предметностью так, что смысл знака и его предмет представлены только самим знаком и раскрываются лишь через его интерпретацию.
С открытием математических правил и теорем ученые придумывали новые математические обозначения, знаки. Математические знаки — это условные обозначения, предназначенные для записи математических понятий, предложений и выкладок. В математике употребляются специальные символы, позволяющие сократить запись и точнее выразить утверждение. Помимо цифр и букв различных алфавитов (латинского, греческого, еврейского) математический язык используют множество специальных символов, изобретенных за последние несколько столетий.
2. Знаки сложения, вычитания
История математических обозначений начинается с палеолита. Этим временем датируются камни и кости с насечками, использовавшимися для счета. Наиболее известный пример — кость Ишанго . Знаменитая кость из Ишанго (Конго) датируемая примерно 20 тысяч лет до новой эры, доказывает, что уже в то время человек выполнял достаточно сложные математические операции. Насечки на кости использовались для сложения и наносились группами, символизируя сложения чисел.
В Древнем Египте была уже намного более продвинутая система обозначений. Например, в папирусе Ахмеса в качестве символа сложения используется изображение двух ног, идущих вперед по тексту, а для вычитания — двух ног, идущих назад. Древние греки обозначали сложение записью рядом, но время от времени использовали для этого символ косой черты “/’’ и полуэллиптическую кривую для вычитания.
Символы для арифметических операций сложения (плюс “+’’) и вычитания (минус “-‘’) встречаются настолько часто, что мы почти никогда не задумываемся о том, что они существовали не всегда. Происхождение этих символов неясно. Одна из версий — они ранее использовались в торговом деле как признаки прибыли и убытка.
Считается, так же, что наш знак происходит от одной из форм слова “et’’, которое по-латыни значит “и’’. Выражение a + b писалось на латыни так: a et b . Постепенно, из-за частого использования, от знака » et » осталось только » t » , которое, со временем превратилось в » + «. Первым человеком, который, возможно, использовал знак как аббревиатуру для et, был астроном Николь д’Орем (автор книги “The Book of the Sky and the World’’ — “Книги неба и мира’’) в середине четырнадцатого века.
В конце пятнадцатого века французский математик Шике (1484 г.) и итальянский Пачоли (1494 г.) использовали “ ’’ или “ ’’ (обозначая “плюс’’) для сложения и “ ’’ или “ ’’ (обозначая “минус’’) для вычитания.
Обозначения вычитания были более запутанными, так как вместо простого знака “ ” в немецких, швейцарских и голландских книгах иногда использовали символ “÷’’, которым мы сейчас обозначаем деление. В нескольких книгах семнадцатого века (например, у Декарта и Мерсенна) использованы две точки “∙ ∙’’ или три точки “∙ ∙ ∙’’ для обозначения вычитания.
Первое использование современного алгебраического знака “ ” относится к немецкой рукописи по алгебре 1481 г., которая была найдена в библиотеке Дрездена. В латинской рукописи того же времени (также из библиотеки Дрездена), есть оба символа: « » и « — » . Систематическое использование знаков « » и « — » для сложения и вычитания встречается у Иоганна Видмана . Немецкий математик Иоганн Видманн (1462-1498) первым использовал оба знака для пометок присутствия и отсутствия студентов на своих лекциях. Правда, есть сведения, что он «позаимствовал» эти знаки у малоизвестного профессора Лейпцигского университета. В 1489 году он издал в Лейпциге первую печатную книгу (Mercantile Arithmetic — “Коммерческая арифметика’’), в которой присутствовали оба знака и , в труде «Быстрый и приятный счёт для всех торговцев» (ок. 1490)
Как исторический курьез, стоит отметить, что даже после принятия знака не все использовали этот символ. Видман сам ввел его как греческий крест (знак, который мы используем сегодня), у которого горизонтальная черта иногда немного длиннее вертикальный. Некоторые математики, такие как Рекорд, Харриот и Декарт, использовали такой же знак. Другие (например, Юм, Гюйгенс, и Ферма) использовали латинский крест « † », иногда расположенный горизонтально, с перекладиной на одном конце или на другом. Наконец, некоторые (например, Галлей) использовали более декоративный вид « ».
3.Знак равенства
Знак равенства в математике и других точных науках пишут между двумя идентичными по своему размеру выражениями. Первым употребил знак равенства Диофант. Равенство он обозначил буквой i (от греческого isos – равный). В античной и средневековой математике равенство обозначалось словесно, например, est egale, или использовали аббревиатуру “ae’’ от латинского aequalis — “равны’’. На других языках также использовали первые буквы слова “равный’’, но это не было общепринятым. Знак равенства «=» ввел в 1557 году уэльский врач и математик Роберт Рекорд (Recorde R., 1510-1558). Математическим символом для обозначения равенства служил в некоторых случаях символ II. Рекорд ввел символ “=’’ с двумя одинаковыми горизонтальными параллельными отрезками, гораздо более длинными, чем те, что используются сегодня. Английский математик Роберт Рекорд был первым, кто начал использовать символ «равенство», аргументируя словами: «никакие два предмета не могут быть равны между собой более, чем два параллельных отрезка». Но ещё в XVII веке Рене Декарт использовал аббревиатуру “ae’’. Франсуа Виет знаком равенства обозначал вычитание. Некоторое время распространению символа Рекорда мешало то обстоятельство, что такой же символ использовался для обозначения параллельности прямых; в конце концов было решено символ параллельности сделать вертикальным. Распространение знак получил только после работ Лейбница на рубеже XVII-XVIII веков, то есть более чем через 100 лет после смерти впервые использовавшего его для этого Роберта Рекорда . На его могильной плите нет слов – просто вырезан знак «равно».
Родственные символы для обозначения приблизительного равенства «≈» и тождества «≡» являются совсем молодыми — первый введен в 1885 году Гюнтером, второй — в 1857 году Риманом
4. Знаки умножения и деления
Знак умножения в виде крестика («х») ввел англиканский священник-математик Уильям Отред в 1631 году . До него для знака умножения использовали букву M, хотя предлагались и другие обозначения: символ прямоугольника (Эригон , ), звёздочка (Иоганн Ран , ).
Позднее Лейбниц заменил крестик на точку (конец XVII века ), чтобы не путать его с буквой x ; до него такая символика встречалась у Региомонтана (XV век ) и английского учёного Томаса Хэрриота (1560-1621).
Для обозначения действия деления Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц . До них часто использовали также букву D. Начиная с Фибоначчи , используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. Деление в виде обелюс («÷») ввел швейцарский математик Иоганн Ран (ок. 1660)
5. Знак процента .
Сотая доля целого, принимаемого за единицу. Само слово «процент» происходит от латинского «pro centum», что означает в переводе «на сто». В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта (1685). В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращённо от cento). Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход.
6.Знак бесконечности
Нынешний символ бесконечности «∞» ввел в употребление Джон Уоллис в 1655 году. Джон Уоллис издал большой трактат «Арифметика бесконечного» (лат. Arithmetica Infinitorum sive Nova Methodus Inquirendi in Curvilineorum Quadraturam, aliaque Difficiliora Matheseos Problemata ), где ввёл придуманный им символ бесконечности . До сих пор так и не известно, почему он остановил свой выбор именно на этом знаке. Одна из наиболее авторитетных гипотез связывает происхождение этого символа с латинской буквой «М», которую римляне использовали для обозначения числа 1000. Символ бесконечности назван «lemniscus» (лат. лента) математиком Бернулли приблизительно сорок лет спустя.
Другая версия говорит о том, что рисунок «восьмерки» передает главное свойство понятия «бесконечность»: движение без конца . По линиям числа 8 можно совершать, как по велотреку, бесконечное движение. Для того, чтобы не путать введенный знак с числом 8, математики решили располагать его горизонтально. Получилось . Такое обозначение cтало стандартным для всей математики, не только алгебры. Почему бесконечность не обозначают нулем? Ответ очевиден: цифру 0 как не поворачивай — она не изменится. Поэтому выбор и пал именно на 8.
Другой вариант — змей, пожирающий свой хвост, который за полторы тысячи лет до нашей эры в Египте символизировал различные процессы, не имеющие начала и конца.
Многие считают, что лист Мёбиуса является прародителем символа бесконечности , т.к символ бесконечности был запатентован после изобретения устройства «лента Мебиуса» (названный в честь математика девятнадцатого столетия Мебиуса). Лента Мебиуса — полоса бумаги, которая искривлена и соединена концами, формируя две пространственные поверхности. Однако по имеющимся историческим сведениям символ бесконечности стал использоваться для обозначения бесконечности за два столетия до открытия ленты Мёбиуса
7. Знаки угл а и перпендикулярно сти
Символы « угол » и « перпендикулярно » придумал в 1634 году французский математик Пьер Эригон . Символ перпендикулярности у него был перевёрнут, напоминая букву T. Символ угла напоминал значок , современную форму ему придал Уильям Отред ().
8. Знак параллельност и
Символ « параллельности » известен с античных времён, его использовали Герон и Папп Александрийский . Сначала символ был похож на нынешний знак равенства, но с появлением последнего, во избежание путаницы, символ был повёрнут вертикально (Отред (1677), Керси (John Kersey ) и др. математики XVII века)
9. Число пи
Общепринятое обозначение числа, равного отношению длины окружности к ее диаметру (3,1415926535…), впервые образовал Уильям Джонс в 1706 году , взяв первую букву греческих слов περιφέρεια — окружность и περίμετρος — периметр , то есть длина окружности. Это сокращение понравилось Эйлеру , труды которого закрепили обозначение окончательно.
10. Синус и косинус
Интересно появление синуса и косинуса.
Sinus с латинского — пазуха, впадина. Но история у такого названия долгая. Далеко в тригонометрии продвинулись индийские математики в районе 5 века. Самого слова «тригонометрия» не было, оно было введено Георгом Клюгелем в 1770 году.) То, что мы сейчас называем синусом, примерно соответствует тому, что индусы называли ардха-джия, в переводе — полутетива (т.е. полухорда). Для краткости называли просто — джия (тетива). Когда арабы переводили работы индусов с санскрита, они не стали переводить «тетиву» на арабский, а просто транскрибировали слово арабскими буквами. Получилась джиба. Но так как в слоговой арабской письменности краткие гласные не обозначаются, то реально остается дж-б, что похоже на другое арабское слово — джайб (впадина, пазуха). Когда Герард Кремонский в 12 веке переводил арабов на латынь, он перевел это слово как sinus, что по-латыни также означает пазуху, углубление.
Косинус появился автоматически, т.к. индусы называли его коти-джия, или сокращено ко-джия. Коти — изогнутый конец лука на санскрите. Современные краткие обозначения и введены Уильямом Отредом и закреплены в трудах Эйлера .
Обозначения тангенса/котангенса имеют намного более позднее происхождение (английское слово tangent происходит от латинского tangere — касаться). И даже до сих пор нет унифицированного обозначения — в одних странах чаще используется обозначение tan, в других — tg
11. Сокращение «Что и требовалось доказать» (ч.т.д.)
«
Quod erat demonstrandum
» (квол эрат лэмонстранлум).
Греческая фраза имеет значение «что требовалось доказывать», а латинская — «что нужно было показать». Этой формулой заканчивается каждое математическое рассуждение великого греческого математика Древней Греции Эвклида (III в. до н. э.). В переводе с латинского — что и требовалось доказать. В средневековых научных трактатах эту формулу писали часто в сокращенном виде: QED.
12. Математические обозначения.
Символы | История символов |
Знаки плюса и минуса придумали, по-видимому, в немецкой математической школе «коссистов» (то есть алгебраистов). Они используются в «Арифметике» Иоганна Видмана изданной в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов неясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа практически мгновенно получили общее распространение в Европе — за исключением Италии. | |
× ∙ | Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали букву M. Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560-1621). |
/ : ÷ | Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц. До них часто использовали также букву D. Начиная с Фибоначчи, используется также черта дроби, употреблявшаяся ещё в арабских сочинениях. В Англии и США распространение получил символ ÷ (обелюс), который предложили Йоханн Ран и Джон Пелл в середине XVII века. |
= | Знак равенства предложил Роберт Рекорд (1510-1558) в 1557 году. Он пояснил, что нет в мире ничего более равного, чем два параллельных отрезка одинаковой длины. В континентальной Европе знак равенства был введён Лейбницем. |
Знаки сравнения ввёл Томас Хэрриот в своём сочинении, изданном посмертно в 1631 году. До него писали словами: больше, меньше. | |
% | Символ процента появляется в середине XVII века сразу в нескольких источниках, его происхождение неясно. Есть гипотеза, что он возник от ошибки наборщика, который сокращение cto (cento, сотая доля) набрал как 0/0. Более вероятно, что это скорописный коммерческий значок, возникший лет на 100 раньше. |
√ | Знак корня впервые употребил немецкий математик Кристоф Рудольф, из школы коссистов, в 1525 году. Происходит этот символ от стилизованной первой буквы слова radix (корень). Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня. |
a
n | Возведение в степень. Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2. Позднее Ньютон распространил эту форму записи на отрицательные и дробные показатели (1676). |
() | Скобки появились у Тартальи (1556) для подкоренного выражения, но большинство математиков предпочитали вместо скобок надчёркивать выделяемое выражение. В общее употребление скобки ввёл Лейбниц. |
Знак суммы ввёл Эйлер в 1755 году | |
Знак произведения ввёл Гаусс в 1812 году | |
i | Букву i как код мнимой единицы:
предложил Эйлер (1777), взявший для этого первую букву слова imaginarius (мнимый). |
π | Общепринятое обозначение числа 3.14159… образовал Уильям Джонс в 1706 году, взяв первую букву греческих слов περιφέρεια — окружность и περίμετρος — периметр, то есть длина окружности. |
Обозначение интеграла Лейбниц произвёл от первой буквы слова «Сумма» (Summa). | |
y» | Краткое обозначение производной штрихом восходит к Лагранжу. |
Символ предела появился в 1787 году у Симона Люилье (1750-1840). | |
Символ бесконечности придумал Валлис, опубликован в 1655 году. |
13. Заключение
Математическая наука необходима для цивилизованного общества. Математика содержится во всех науках. Математический язык смешивается с языком химии и физики. Но нам он все равно понятен. Можно сказать, что язык математики мы начинаем изучать вместе с родной речью. Так неразрывно вошла математика в нашу жизнь. Благодаря математическим открытиям прошлого, ученые создают новые технологии. Сохранившиеся открытия дают возможность решать сложные математически задачи. И древний математический язык нам понятен, а открытия нам интересны. Благодаря математике Архимед, Платон, Ньютон открыли физические законы. Мы изучаем их в школе. В физике тоже есть символы термины присущие физической науке. Но математический язык не теряется среди физических формул. Наоборот, эти формулы нельзя написать без знания математики. Благодаря истории сохраняются знания и факты для будущих поколений. Дальнейшее изучение математики необходимо для новых открытий. Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Математические символы Работу выполнил ученик 7-а класса школы №574 Балагин Виктор
Символ (греч. symbolon – признак, примета, пароль, эмблема) – знак, который связан с обозначаемой им предметностью так, что смысл знака и его предмет представлены только самим знаком и раскрываются лишь через его интерпретацию. Знаки – это математические условные обозначения, предназначенные для записи математических понятий, предложений и выкладок.
Кость Ишанго Часть папируса Ахмеса
+ − Знаки плюса и минуса. Сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). Выражение a + b писалось на латыни так: a et b .
Обозначения вычитания. ÷ ∙ ∙ или ∙ ∙ ∙ Рене Декарт Марен Мерсенн
Страница из книги Иоганна Видман н а. В 1489 году Иоганн Видман издал в Лейпциге первую печатную книгу (Mercantile Arithmetic — “ Коммерческая арифметика’’), в которой присутствовали оба знака + и —
Обозначения сложения. Христиан Гюйгенс Дэвид Юм Пьер де Ферма Эдмунд (Эдмонд) Галлей
Знак равенства Первым употребил знак равенства Диофант. Равенство он обозначил буквой i (от греческого isos – равный).
Знак равенства Предложил в 1557 году английский математик Роберт Рекорд «Никакие два предмета не могут быть равны между собой более, чем два параллельных отрезка». В континентальной Европе знак равенства был введён Лейбницем
× ∙ Знак умножения Ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x . Уильям Отред Готфрид Вильгельм Лейбниц
Процент. Матье де ла Порт (1685). Сотая доля целого, принимаемого за единицу. «процент» — «pro centum», что означает — «на сто». «cto» (сокращённо от cento). Н аборщик принял «cto» за дробь и напечатал «%».
Бесконечность. Джон Уоллис Джон Уоллис в 1655 году ввёл придуманный им символ. Змей, пожирающий свой хвост, символизировал различные процессы, не имеющие начала и конца.
Символ бесконечности стал использоваться для обозначения бесконечности за два столетия до открытия ленты Мёбиуса Лента Мебиуса – полоса бумаги, которая искривлена и соединена концами, формируя две пространственные поверхности. Август Фердинанд Мёбиус
Угол и перпендикуляр. Символы придумал в 1634 году французский математик Пьер Эригон. Символ угла у Эригона напоминал значок. Символ перпендикулярности был перевёрнут, напоминая букву T . Современную форму этим знакам придал Уильям Отред (1657).
Параллельность. Символ использовали Герон Александрийский и Папп Александрийский. Сначала символ был похож на нынешний знак равенства, но с появлением последнего, во избежание путаницы, символ был повёрнут вертикально. Герон Александрийский
Число пи. π ≈ 3,1415926535… Уильям Джонс в 1706 году π εριφέρεια -окружность и π ερίμετρος — периметр, то есть длина окружности. Это сокращение понравилось Эйлеру, труды которого закрепили обозначение окончательно. Уильям Джонс
sin Синус и косинус cos Sinus (с латинского) – пазуха, впадина. коти-джия, или сокращено ко-джия. Коти — изогнутый конец лука Современные краткие обозначения введены Уильямом Отредом и закреплены в трудах Эйлера. «арха-джива» — у индийцев -«полутетива» Леонард Эйлер Уильям Отред
Что и требовалось доказать (ч.т.д.) « Quod erat demonstrandum » QED. Этой формулой заканчивается каждое математическое рассуждение великого математика Древней Греции Эвклида (III в. до н. э.).
Древний математический язык нам понятен. В физике тоже есть символы термины присущие физической науке. Но математический язык не теряется среди физических формул. Наоборот, эти формулы нельзя написать без знания математики.
Математические обозначения («язык математики ») — сложная графическая система обозначений, служащая для изложения абстрактных математических идей и суждений в человеко-читаемой форме. Составляет (по своей сложности и разнообразию) значительную долю неречевых знаковых систем , применяемых человечеством. В данной статье описывается общепринятая международная система обозначений, хотя различные культуры прошлого имели свои собственные, и некоторые из них даже имеют ограниченное применение до сих пор.
Отметим, что математические обозначения, как правило, применяются совместно с письменной формой какого-то из естественных языков .
Помимо фундаментальной и прикладной математики, математические обозначения имеют широкое применение в физике , а также (в неполном своём объёме) в инженерии , информатике , экономике , да и вообще во всех областях человеческой деятельности, где применяются математические модели . Различия между собственно математическим и прикладным стилем обозначений будут оговорены по ходу текста.
Энциклопедичный YouTube
1 / 5
✪ Знак / в математике
✪ Математика 3 класс. Таблица разрядов многозначных чисел
✪ Множества в математике
✪ Математика 19. Математические забавы — Шишкина школа
Субтитры
Привет! Это видео не о математике, скорее об этимологии и семиотике. Но уверен, вам понравится. Поехали! Вы вот в курсе, что поиск решения кубических уравнений в общем виде занял у математиков несколько столетий? Это отчасти почему? Потому что не было ясных символов для ясных мыслей, то ли дело наше время. Символов столько, что и запутаться можно. Но нас с вами не проведешь, давайте разбираться. Вот это — заглавная перевернутая буква А. Это на самом деле английская буква, числится первой в словах «all» и «any». По-русски этот символ, в зависимости от контекста, может читаться так: для любого, всякий, каждому, все и так далее. Такой иероглиф будем называть квантором всеобщности. А вот и еще один квантор, но уже существование. Английскую букву е отразили в Paint-е слева направо, намекая тем самым на заморский глагол «exist», по-нашему будем читать: существует, найдется, имеется и другим подобным образом. Восклицательный знак такому квантору существования добавит единственности. Если с этим понятно, двигаемся дальше. Неопределенные интегралы вам наверняка попадались в классе так одиннадцатом, я бы хотел напомнить, что это не просто какая-то первообразная, а совокупность всех первообразных подынтегральной функции. Так что не забывайте про С — константу интегрирования. Между делом, сам значок интеграла — это просто вытянутая буква s, отголосок латинского слова сумма. В этом как раз и есть геометрический смысл определенного интеграла: поиск площади фигуры под графиком суммированием бесконечно малых величин. Как по мне, это самое романтичное занятие в матанализе. А вот школьная геометрия полезнее всего тем, что приучает к логической строгости. К первому курсу у вас должно быть чёткое понимание, что такое следствие, что такое равносильность. Ну нельзя путаться в необходимости и достаточности, понимаете? Давайте даже попробуем копнуть чуть-чуть глубже. Если вы решили заняться высшей математикой, то я представляю, насколько у вас все плохо с личной жизнью, но именно поэтому вы наверняка согласитесь одолеть небольшое упражнение. Здесь три пункта, в каждом имеется левая и правая части, которую вам нужно связать одним из трех нарисованных символов. Пожалуйста, кликните паузу, попробуйте сами, а затем послушайте, что я вам скажу. Если x=-2, то |x|=2, а вот слева направо так фразу уже построить. Во втором пункте в левой и правой частях написано абсолютно одно и то же. А третий пункт можно прокомментировать так: каждый прямоугольник является параллелограммом, но не каждый параллелограмм является прямоугольником. Да, знаю, что вы уже не маленькие, но все же мои аплодисменты тем, кто справился с этим упражнением. Ну да ладно, хватит, давайте вспомним числовые множества. Натуральные числа используются при счете: 1, 2, 3, 4 и так далее. В природе -1 яблока не существует, но, кстати, целые числа позволяют говорить о таких вещах. Буква ℤ кричит нам о важной роли нуля, множество рациональных чисел обозначается буквой ℚ, и это неслучайно. В английском слово «quotient» означает «отношение». Кстати, если где-нибудь в Бруклине к вам подойдет афроамериканец и скажет: «Keep it real!», — можете быть уверены, перед вами математик, почитатель действительных чисел. Ну а вам стоит почитать что-нибудь о комплексных числах, будет полезней. Мы же сейчас сделаем откат, вернемся в первый класс самой что ни на есть обычной греческой школы. Короче говоря, помянем древний алфавит. Первая буква — альфа, затем бетта, этот крючок — гамма, потом дельта, после неё следует эпсилон и так далее, вплоть до последней буквы омега. Можете не сомневаться, что у греков есть и прописные буквы, но мы сейчас не будем о грустном. Мы лучше о веселом — о пределах. Но тут как раз никаких загадок и нет, сразу понятно, от какого слова появился математический символ. Ну а стало быть, мы можем перейти к финальной части видео. Пожалуйста, попробуйте озвучить определение предела числовой последовательности, которое сейчас написано перед вами. Кликайте скорее паузу и соображаете, и да будет вам счастье годовалого ребенка, узнавшего слово «мама». Если для любого эпсилон больше нуля найдется натуральное N, да такое, что для всех номеров числовой последовательности, больших N, выполнено неравенство |xₙ-a|
Общие сведения
Система складывалась, наподобие естественных языков, исторически (см. история математических обозначений), и организована наподобие письменности естественных языков, заимствуя оттуда также многие символы (прежде всего, из латинского и греческого алфавитов). Символы, также как и в обычной письменности, изображаются контрастными линиями на равномерном фоне (чёрные на белой бумаге, светлые на тёмной доске, контрастные на мониторе и т. д.), и значение их определяется в первую очередь формой и взаимным расположением. Цвет во внимание не принимается и обычно не используется, но, при использовании букв , такие их характеристики как начертание и даже гарнитура , не влияющие на смысл в обычной письменности, в математических обозначениях могут играть смыслоразличающую роль.
Структура
Обыкновенные математические обозначения (в частности, так называемые математические формулы ) пишутся в общем в строку слева направо, однако не обязательно составляют последовательную строку символов. Отдельные блоки символов могут располагаться в верхней или нижней половине строки, даже в случае, когда символы не перекрываются вертикалями. Также, некоторые части располагаются целиком выше или ниже строки. С грамматической же стороны почти любую «формулу» можно считать иерархически организованной структурой типа дерева .
Стандартизация
Математические обозначения представляют систему в смысле взаимосвязи своих компонент, но, в целом, не составляют формальную систему (в понимании самой математики). Они, в сколь-нибудь сложном случае, не могут быть даже разобраны программно . Как и любой естественный язык, «язык математики» полон несогласованных обозначений, омографов , различных (в среде своих носителей) трактовок того, что́ считать правильным и т. п. Нет даже сколь-нибудь обозримого алфавита математических символов, и в частности оттого, что не всегда однозначно решается вопрос, считать ли два обозначения разными символами или же разными написаниями одного символа.
Некоторая часть математических обозначений (в основном, связанная с измерениями) стандартизована в ISO 31 -11, однако в целом стандартизация обозначений скорее отсутствует.
Элементы математических обозначений
Числа
При необходимости применить систему счисления с основанием , меньшим десяти, основание записывается в нижний индекс: 20003 8 . Системы счисления с основаниями, бо́льшими десяти, в общепринятой математической записи не применяются (хотя, разумеется, изучаются самой наукой), поскольку для них не хватает цифр. В связи с развитием информатики , стала актуальной шестнадцатеричная система счисления , в которой цифры от 10 до 15 обозначаются первыми шестью латинскими буквами от A до F. Для обозначения таких чисел в информатике используется несколько разных подходов, но в математику они не перенесены.
Надстрочные и подстрочные знаки
Скобки, подобные им символы и разделители
Круглые скобки «()» используются:
Квадратные скобки «» нередко применяются в значении группировки, когда приходится использовать много пар скобок. В таком случае они ставятся снаружи и (при аккуратной типографике) имеют бо́льшую высоту, чем скобки, стоя́щие внутри.
Квадратные «» и круглые «()» скобки используются при обозначении закрытых и открытых промежутков соответственно.
Фигурные скобки «{}» используются, как правило, для , хотя в отношении них справедлива та же оговорка, что и для квадратных скобок. Левая «{» и правая «}» скобки могут использоваться по отдельности; их назначение описано .
Символы угловых скобок « ⟨ ⟩ {\displaystyle \langle \;\rangle } » при аккуратной типографике должны иметь тупые углы и тем отличаться от схожих , имеющих прямой или острый угол. На практике же на это не следует надеяться (особенно, при ручной записи формул) и различать их приходится при помощи интуиции.
Часто используются пары симметричных (относительно вертикальной оси) символов, в том числе и отличных от перечисленных, для выделения куска формулы. Назначение парных скобок описано .
Индексы
В зависимости от расположения различают верхние и нижние индексы. Верхний индекс может означать (но необязательно означает) возведение в степень , об остальных случаях использования .
Переменные
В науках встречаются наборы величин, и любая из них может принимать или набор значений и называться переменной величиной (вариантой), или только одно значение и называться константой. В математике от физического смысла величины часто отвлекаются, и тогда переменная величина превращается в отвлечённую (или числовую) переменную, обозначаемую каким-нибудь символом, не занятым специальными обозначениями, о которых было сказано выше.
Переменная X считается заданной, если указано множество принимаемых ею значений {x} . Постоянную же величину удобно рассматривать как переменную, у которой соответствующее множество {x} состоит из одного элемента.
Функции и операторы
В математике не усматривается существенного различия между оператором (унарным), отображением и функцией .
Однако, подразумеваются, что если для записи значения отображения от заданных аргументов необходимо указывать , то символ оного отображения обозначает функцию, в иных случаях скорее говорят об операторе. Символы некоторых функций одного аргумента употребляются и со скобками и без. Многие элементарные функции , например sin x {\displaystyle \sin x} или sin (x) {\displaystyle \sin(x)} , но элементарные функции всегда называются функциями .
Операторы и отношения (унарные и бинарные)
Функции
Функция может упоминаться в двух смыслах: как выражение её значения при заданных аргументах (пишется f (x) , f (x , y) {\displaystyle f(x),\ f(x,y)} и т. п.) или собственно как функция. В последнем случае ставится только символ функции, без скобок (хотя зачастую пишут как попало).
Имеется много обозначений общепринятых функций, используемых в математических работах без дополнительных пояснений. В противном случае функцию надо как-то описывать и в фундаментальной математике она принципиально не отличается от и точно также обозначается произвольной буквой. Для обозначения функций-переменных наиболее популярна буква f , также часто применяются g и большинство греческих.
Предопределённые (зарезервированные) обозначения
Однако, однобуквенным обозначениям может быть, при желании, придан другой смысл. Например, буква i часто используется как обозначение индекса в контексте, где комплексные числа не применяются, а буква может быть использована как переменная в какой-нибудь комбинаторике . Также, символы теории множеств (такие как « ⊂ {\displaystyle \subset } » и « ⊃ {\displaystyle \supset } ») и исчисления высказываний (такие как « ∧ {\displaystyle \wedge } » и « ∨ {\displaystyle \vee } ») могут быть использованы в другом смысле, обычно как отношение порядка и бинарные операции соответственно.
Индексирование
Индексирование графически изображается (обычно нижними, иногда и верхними) и является, в некоторым смысле, способом расширить информационное наполнение переменной. Однако, употребляется оно в трёх несколько различных (хотя и перекрывающихся) смыслах.
Собственно номера
Можно иметь несколько разных переменных, обозначая их одной буквой, аналогично использованию . Например: x 1 , x 2 , x 3 … {\displaystyle x_{1},\ x_{2},\ x_{3}\ldots } . Обычно они связаны какой-то общностью, но вообще это не обязательно.
Более того, в качестве «индексов» можно использовать не только числа, но и любые символы. Однако, когда в виде индекса пишется другая переменная и выражение, данная запись интерпретируется как «переменная с номером, определяемым значением индексного выражения».
В тензорном анализе
В линейной алгебре , тензорном анализе , дифференциальной геометрии с индексами (в виде переменных) записываются
Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как знак больше и знак меньше , а также знак равно.
Однако, если с последним что-то напутать достаточно сложно, то о том, как и в какую сторону пишутся знаки больше и меньше (знак менее и знак более , как ещё их иногда называют) многие сразу после этой же школьной скамьи и забывают, т.к. они довольно редко используются нами в повседневной жизни.
Но практически каждому рано или поздно всё равно приходится столкнуться с ними, и «вспомнить» в какую сторону пишется нужный им символ получается лишь обратившись за помощью к любимой поисковой системе. Так почему бы не ответить развернуто на этот вопрос, заодно подсказав посетителям нашего сайта как запомнить правильное написание этих знаков на будущее?
Именно о том, как правильно пишется знак больше и знак меньше мы и хотим напомнить вам в этой небольшой заметке. Также будет не лишним рассказать и том, как набрать на клавиатуре знаки больше или равно и меньше или равно , т.к. этот вопрос тоже довольно часто вызывает затруднения у пользователей, сталкивающихся с такой задачей очень редко.
Перейдем сразу к делу. Если вам не очень интересно запоминать всё это на будущее и проще в следующий раз снова «погуглить», а сейчас просто нужен ответ на вопрос «в какую сторону писать знак», тогда для вас мы приготовили краткий ответ — знаки больше и меньше пишутся так, как показано на изображении ниже.
А теперь расскажем немного подробнее о том, как это понять и запомнить на будущее.
В общем и целом логика понимания очень проста — какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону — такой и знак. Соответственно, знак больше влево смотрит широкой стороной — большей.
Пример использования знака больше:
- 50>10 — число 50 больше числа 10;
- посещаемость студента в этом семестре составила >90% занятий.
Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной — меньшей, то перед вами знак меньше.
Пример использования знака меньше:
- 100
- на заседание явилось
Как видите, все довольно логично и просто, так что теперь вопросов о том, в какую сторону писать знак больше и знак меньше в будущем у вас возникать не должно.
Знак больше или равно/меньше или равно
Если вы уже вспомнили, как пишется необходимый вам знак, то дописать к нему одну черточку снизу вам не составит труда, таким образом вы получите знак «меньше или равно» или знак «больше или равно» .
Однако относительно этих знаков у некоторых возникает другой вопрос — как набрать такой значок на клавиатуре компьютера? В результате большинство просто ставят два знака подряд, к примеру, «больше или равно» обозначая как «>=» , что, в принципе, часто вполне допустимо, но можно сделать красивее и правильнее.
На самом деле для того, чтобы напечатать эти знаки, существуют специальные символы, которые можно ввести на любой клавиатуре. Согласитесь, знаки «≤» и «≥» выглядят значительно лучше.
Знак больше или равно на клавиатуре
Для того, чтобы написать «больше или равно» на клавиатуре одним знаком даже не нужно лезть в таблицу специальных символов — просто поставьте знак больше с зажатой клавишей «alt» . Таким образом сочетание клавиш (вводится в английской раскладке) будет следующим.
Или же вы можете просто скопировать значок из этой статьи, если вам нужно воспользоваться им один раз. Вот он, пожалуйста.
≥
Знак меньше или равно на клавиатуре
Как вы наверное уже смогли догадаться сами, написать «меньше или равно» на клавиатуре вы можете по аналогии со знаком больше — просто поставьте знак меньше с зажатой клавишей «alt» . Сочетание клавиш, которое нужно вводить в английской раскладке, будет следующим.
Или просто скопируйте его с этой страницы, если вам так будет проще, вот он.
≤
Как видите, правило написания знаков больше и меньше довольно просто запомнить, а для того чтобы набрать значки больше или равно и меньше или равно на клавиатуре достаточно просто нажать дополнительную клавишу — всё просто.
В абстрактной алгебре повсеместно используются символы для упрощения и сокращения текста, а также стандартные обозначения для некоторых групп. Ниже приведён список наиболее часто встречающихся алгебраических обозначений, соответствующие команды в … Википедия
Математические обозначения это символы, используемые для компактной записи математических уравнений и формул. Помимо цифр и букв различных алфавитов (латинского, в том числе в готическом начертании, греческого и еврейского),… … Википедия
Статья содержит список общеупотребительных аббревиатур математических функций, операторов и др. математических терминов. Содержание 1 Аббревиатуры 1.1 Латиница 1.2 Греческий алфавит … Википедия
Юникод, или Уникод (англ. Unicode) стандарт кодирования символов, позволяющий представить знаки практически всех письменных языков. Стандарт предложен в 1991 году некоммерческой организацией «Консорциум Юникода» (англ. Unicode Consortium,… … Википедия
Список используемых в математике специфических символов можно увидеть в статье Таблица математических символов Математические обозначения («язык математики») сложная графическая система обозначений, служащая для изложения абстрактных… … Википедия
У этого термина существуют и другие значения, см. Плюс минус (значения). ± ∓ Знак плюс минус (±) математический символ, который ставится перед некоторым выражением и означает, что значение этого выражения может быть как положительным, так и … Википедия
Необходимо проверить качество перевода и привести статью в соответствие со стилистическими правилами Википедии. Вы можете помочь … Википедия
Или математические символы знаки, которые символизируют определённые математические действия со своими аргументами. К самым распространённым относятся: Плюс: + Минус: , − Знак умножения: ×, ∙ Знак деления: :, ∕, ÷ Знак возведения в… … Википедия
Знаки операций или математические символы знаки, которые символизируют определённые математические действия со своими аргументами. К самым распространённым относятся: Плюс: + Минус: , − Знак умножения: ×, ∙ Знак деления: :, ∕, ÷ Знак возведения… … Википедия
больше, чем символ в математике: примеры | Что такое знак «больше»? — Видео и стенограмма урока
Разница между знаками «больше» и «меньше»
Так как есть знак «больше», то существует на знак «меньше» , и они противоположны друг другу. При чтении слева направо знак «меньше» является частью утверждения, говорящего о том, что одна вещь меньше или меньше другой. Знаки «больше» и «меньше» выглядят одинаково, но обращены в противоположные стороны.
Знак «Больше»:>
Знак «Меньше»: <
Оба знака имеют форму стрелки. Широкий конец называется открытым концом, и для обоих символов открытый конец будет указывать на большее число.
$$ 100> 50 $$
$$ 50 <100 $$
Вкратце:
- Знак «больше» открывается слева.
- Знак «меньше» открывается вправо.
- В числовом выражении читайте слева направо, поскольку два знака означают противоположные вещи.
Способы запомнить большее, чем меньше, чем символы
Поскольку два знака имеют одинаковую форму, может возникнуть путаница в том, какой знак какой. Есть несколько полезных стратегий.
Метод аллигатора
Знаки больше и меньше, будучи открытыми с одного конца, напоминают открытую пасть. Фактически, мы можем представить, что оба знака — голодные аллигаторы с широко раскрытой пастью. Голодный аллигатор всегда целится своей открытой пастью в большее количество рыб.
L-метод
Рассмотрим это математическое утверждение:
$$ 10 <40 $$
Это можно прочитать вслух как «Десять меньше сорока».
При использовании метода L мы берем букву L в слове «меньше чем» и заменяем ее знаком «меньше».Знак «меньше чем» выглядит как L, так что это работает. Знак больше не похож на букву L, поэтому он не работает.
Метод знака равенства
Добавление строки под знаком «больше» может превратить его в больше или равно знаку . Знак «больше» здесь
$$ X> 30 $$
означает, что X не 30, а какое-то большее число.
Здесь стоит знак «больше или равно»
$$ X \ geq 30 $$
Означает, что X может быть 30 или больше.
То же самое для знака «меньше». Горизонтальная линия под ним превращает его в , меньшее или равное знаку .
Способ отличить символы «больше или равно» — это метод равенства. Горизонтальная линия под символом стрелки — это всего лишь половина знака равенства, поэтому значения двух символов объединены.
Примеры знаков «больше»
Знак «больше» широко используется в математике. Помните о различиях между знаками больше и меньше.
| Знак / символ | Имя | Описание | Пример | Математическое выражение |
| > | Знак больше | Открывается налево. Открывается в сторону большего числа. | У Тодда 7 пончиков, а у Стива только 3 пончика. | 7> 3 |
| < | Знак меньше | Открывается вправо. Открывается в сторону большего числа. | Тина пробежала 5 миль, а Келли — 9 миль. | 5 <9 |
| = | Знак равенства | Две горизонтальные линии | Бобу и его брату-близнецу Тому по 33 года. | 33 = 33 |
Знаки «больше» и «меньше» также могут использоваться в алгебре, чтобы показать, что неизвестное значение больше или меньше известного.
Марк, Гарри и Линда объединяют свои деньги, чтобы арендовать багги. Марк кладет 30 долларов на прилавок, Линда кладет 25, а Гарри роняет пачку скомканных купюр. Они получают багги для дюн и некоторые мелочи обратно. Гарри не знает, сколько денег он положил, но знает, что это было больше 45 долларов.
$$ X> 45 $$
Советы по устранению неравенств
Неравенства используются, когда известно, что две вещи не равны. В простой математике знак «больше» напрямую показывает взаимосвязь между двумя разными значениями, показывая, какое из них больше.В алгебре неравенство может показать, что неизвестное значение может быть диапазоном возможных значений.
$$ 3x> 27 $$
Решение этого уравнения дает
$$ x> 9 $$
, что означает, что x может быть любым числом, если оно больше 9.
Неравенства также могут включать в себя больше чем два значения. Между последовательными значениями можно поставить несколько знаков больше
$$ 120> 50> 4> 1 $$
В алгебре этот метод может ограничить переменную между двумя значениями
$$ 3 означает, что x может быть любым значением от 3 до 10. Одно неравенство уже было решено выше. В общем, решение неравенства очень похоже на решение уравнения. Применяются те же правила решения уравнений алгебры, а также порядок операций. Главное отличие, которое следует запомнить, заключается в том, что при умножении или делении отрицательного числа в неравенстве знак переворачивается и меняет направление. Знак «больше» станет знаком «меньше», и наоборот. $$ — 3x <42 $$ $$ x> -14 $$ Знак «больше» означает, что одно значение больше другого в неравенстве.Противоположным этому знаку является знак «меньше». Используется напрямую, знак «больше» просто указывает, какое значение больше. В алгебре знак «больше» показывает, что переменная может иметь диапазон значений. Знак «больше или равно» — это знак «больше» с горизонтальной чертой под ним. Этот символ показывает, что диапазон значений переменной превышает определенное число и также включает это число.Точно так же знак «меньше» может превратиться в знак «меньше или равно». Неравенства могут быть решены в алгебре так же, как уравнения, с одним отличием: Помимо знакомого знака равенства ( = ), также очень полезно показать, не равно ли что-то ( ≠ ) больше (> ) или меньше ( <) В математике равенство — это отношение между 2 или более величинами (обычно 2 математическими выражениями), в которых утверждается, что выражения представляют один и тот же математический объект или что величины имеют одинаковое значение. Равенство между X и Y записывается как X = Y, и произносится как X равно Y. Символ «=» называется «знаком равенства». Неравенство — это отношение, которое выполняется между двумя значениями, когда они различны. Запись x ≠ y означает, что x не равно y. Это не говорит о том, что один больше другого, или даже о том, что их можно сравнивать по размеру. Значения, являющиеся элементами упорядоченного набора (например, действительные числа или целые числа), можно сравнивать по размеру. Запись x Знаки «больше» и «меньше» выглядят как буква «v» на своей стороне. Чтобы запомнить, в какую сторону идут знаки «<» и «>», просто запомните: Иногда мы знаем, что значение больше, но также может быть равно! Чтобы показать это, мы добавляем дополнительную строку внизу символа « больше » или « меньше » следующим образом: Знак « больше или равно »: ≥ Знак « меньше или равно »: ≤ Иногда мы можем сказать 2 (или более) вещи в одной строке: Базовая математика Концентрические круги По возрастанию и убыванию2 В чем разница? Когда мы должны использовать «больше, чем» , а когда мы должны использовать «больше, чем» ? А как насчет «меньше чем» или «меньше чем»? Есть разница? Да. Ответ частично заключается в том, СЧЕТНО ли что-то или НЕ СЧЕТНО 1) Если СЧЕТНО (собаки, квартиры, возможности, агентства, люди) -> затем используйте БОЛЬШЕ / МЕНЬШЕ, чем комбинация 2) Если СЧЕТНО , , но связано со временем, расстоянием или деньгами ИЛИ, если НЕ СЧЕТНО -> затем используйте БОЛЬШЕ / МЕНЬШЕ, чем комбинация 3) Для ОБЕИХ СЧЕТНЫХ И НЕ СЧЕТНЫХ , если проводится сравнение УРОВНЯ, СТЕПЕНИ или ЧИСЛА чего-то -> затем используйте комбинацию БОЛЬШЕ / МЕНЬШЕ, ЧЕМ Итак, есть только 3 возможных комбинации: Для счетных слов используйте опцию № 1: БОЛЬШЕ / МЕНЬШЕ чем. Для слов, которые связаны со временем, деньгами или расстоянием ИЛИ не подсчитываются, используйте вариант № 2: БОЛЬШЕ / МЕНЬШЕ, чем Для слов, которые структурно расположены таким образом, что выполняется сравнение между уровнем / степенью / количеством чего-либо, используйте вариант № 3: БОЛЬШЕ / МЕНЬШЕ чем. Вот и все — это единственные 3 возможные комбинации. Действительно, варианты №1 и №2 охватывают большинство ситуаций. Вариант №3 больше связан со структурой. Да, просто изменение структуры предложения может заставить вас перейти от двух вариантов по умолчанию БОЛЬШЕ / МЕНЬШЕ или БОЛЬШЕ / МЕНЬШЕ -> к варианту № 3: БОЛЬШЕ / МЕНЬШЕ Например, давайте использовать слово ЛЮБОВЬ. Если мы хотим сравнить степень любви одного и другого, это будет выглядеть так: 1) Моя любовь БОЛЬШЕ / МЕНЬШЕ, чем любовь x ». Можно ли сказать ту же мысль — но вместо использования комбинации БОЛЬШЕ / МЕНЬШЕ, чем, мы используем комбинацию БОЛЬШЕ / МЕНЬШЕ или БОЛЬШЕ / МЕНЬШЕ? Да, это возможно. Так как ЛЮБОВЬ — слово, которое не исчисляется, мы не можем использовать комбинацию БОЛЬШЕ / МЕНЬШЕ. Нам пришлось бы использовать комбинацию БОЛЬШЕ / МЕНЬШЕ. Итак, это будет выглядеть так: 2) У меня БОЛЬШЕ / МЕНЬШЕ любви, чем у тебя » Обратите внимание, что оба предложения говорят о ЛЮБВИ — НЕ СЧЕТНОЙ вещи — но в первом примере вы сравниваете степень «моей любви» со степенью «любви x» — тогда как во втором примере вы просто говорите что «У меня БОЛЬШЕ / МЕНЬШЕ любви, чем у вас». Итак, у вас есть 2 варианта. БОЛЬШЕ / МЕНЬШЕ или БОЛЬШЕ / МЕНЬШЕ, когда речь идет о слове ЛЮБОВЬ. Другой вариант БОЛЬШЕ / МЕНЬШЕ неприменим. 1) Количество возможностей, которые у него есть, БОЛЬШЕ / МЕНЬШЕ, чем x Да, это возможно. Хотя слово «возможности» можно исчислить, оно заключено во фразе «количество возможностей.«Вот почему мы должны использовать БОЛЬШЕ / МЕНЬШЕ, чем указано выше. Если мы не хотим использовать комбинацию БОЛЬШЕ / МЕНЬШЕ, тогда мы должны изменить СТРУКТУРУ фразы. Таким образом, вместо того, чтобы говорить «количество возможностей», мы должны изменить его на: 2) У него БОЛЬШЕ / МЕНЬШЕ возможностей, чем у х. Поскольку «возможности» можно подсчитать — и мы не имеем дело с уровнем / степенью / или количеством — ситуации, мы можем использовать стандартную комбинацию БОЛЬШЕ / МЕНЬШЕ. Отсюда можно сказать: У него больше возможностей, чем у х. или У него меньше возможностей, чем у x. НО при сравнении уровня, степени или количества — используйте БОЛЬШЕ / МЕНЬШЕ СЧЕТНЫЕ слова включают: человек, телефоны, елки, двери, автомобили, рождественские огни, обеды, домашние хозяйства и т. Д. Более 5 собак ( правильный ) Да, вы можете спросить: «Сколько собак?» — , следовательно, используйте БОЛЬШЕ / МЕНЬШЕ, ЧЕМ Более 5 квартир ( правильно ) Да, вы можете спросить: «Сколько квартир?» — , следовательно, используйте БОЛЬШЕ / МЕНЬШЕ, ЧЕМ Более 5 подруг ( правильных ) Да, вы можете спросить: «Сколько подружек?» — , следовательно, используйте БОЛЬШЕ / МЕНЬШЕ, ЧЕМ Примечание для счетных слов — это довольно просто.Просто используйте комбинацию БОЛЬШЕ / МЕНЬШЕ ЧЕМ по умолчанию. НЕ используйте комбинацию БОЛЬШЕ / МЕНЬШЕ. Единственная разница заключается в МЕНЬШЕ и МЕНЬШЕ для этих счетных слов. Но если вы думаете об использовании БОЛЬШЕ или БОЛЬШЕ ЧЕМ — почти всегда используйте БОЛЬШЕ, ЧЕМ. Вы используете «БОЛЬШЕ» только тогда, когда вы структурируете фразу таким образом, чтобы сравнивать уровень / степень / или номер элемента, на который вы ссылаетесь. Вкратце — для СЧЕТНОГО слова используйте БОЛЬШЕ / МЕНЬШЕ. НО при сравнении уровня, степени или количества — используйте БОЛЬШЕ / МЕНЬШЕ Несчетные слова включают: земля, любовь, деньги, вода, информация, счастье, время, хорошее поведение, строительные материалы ЛЮБОВЬ -> Используйте БОЛЬШЕ / МЕНЬШЕ, ЧЕМ У меня на БОЛЬШЕ любви к ней , чем у тебя. ( правильный ) — из-за НЕ задействованного уровня или степени -> используйте БОЛЬШЕ, ЧЕМ Мой [уровень или степень] любви (НЕ подсчитываемой) к ней БОЛЬШЕ, чем ваша. (неправильно) Вкратце (ЛЮБОВЬ): 1) Моя [уровень или степень] любви (НЕ подсчитываемая) к ней на [БОЛЬШЕ / МЕНЬШЕ] , чем ваша. ( правильно ) — из-за уровня или степени ЗЕМЛЯ -> Используйте БОЛЬШЕ / МЕНЬШЕ, ЧЕМ У меня БОЛЬШЕ земли, чем у вас ( правильно ) У меня МЕНЬШЕ земли, чем у вас (неверно) [Уровень или степень] плодородия моей земли БОЛЬШЕ, чем у вашей земли.(неправильно) Итого (земля): 1) У меня на БОЛЬШЕ / МЕНЬШЕ земли, чем у вас ( правильно ) СЧАСТЬЯ -> Используйте БОЛЬШЕ / МЕНЬШЕ, ЧЕМ Сейчас у меня БОЛЬШЕ счастья, чем когда-либо. (неправильно) Мое [уровень или степень] счастья (НЕ подсчитываемое) БОЛЬШЕ, чем его. (неправильно) Итог (счастье): 1) Сейчас у меня на БОЛЬШЕ / МЕНЬШЕ счастья, чем когда-либо. ( правильный ) ВРЕМЯ (независимо от счетного или несчетного) -> Используйте БОЛЬШЕ / МЕНЬШЕ, ЧЕМ Но если сравниваете уровень, степень или количество — тогда используйте БОЛЬШЕ / МЕНЬШЕ У меня на БОЛЬШЕ раза (НЕ подсчитывается), чем мне нужно. ( правильный ) Я изучаю БОЛЬШЕ , чем 40 минут в день.( правильно ) Итого (время): 1) У меня на БОЛЬШЕ / МЕНЬШЕ времени, чем мне нужно. ДЕНЬГИ (независимо от того, счетные или несчетные) -> Используйте БОЛЬШЕ / МЕНЬШЕ Но если сравниваете уровень, степень или количество — тогда используйте БОЛЬШЕ / МЕНЬШЕ, ЧЕМ РАССТОЯНИЕ (независимо от исчисляемого или неисчисляемого) -> Используйте БОЛЬШЕ / МЕНЬШЕ, ЧЕМ Но если сравниваете уровень, степень или количество — тогда используйте БОЛЬШЕ / МЕНЬШЕ У меня осталось БОЛЕЕ 3 миль. ( правильно ) Итого (расстояние): 1) У меня осталось БОЛЬШЕ / МЕНЬШЕ 3 миль. Используйте БОЛЬШЕ / МЕНЬШЕ ЧЕМ — при сравнении # из: Количество яблок БОЛЬШЕ, чем количество апельсинов. (неверно) Количество яблок БОЛЬШЕ, чем количество апельсинов. (правильно) Количество яблок МЕНЬШЕ, чем количество апельсинов.(неверно) Проценты — это числа, верно? Итак, поскольку они относятся к одной величине, это должно означать, что то, что следует далее, СЧЁТНО, верно? Или это потому, что есть число — значит, оно СЧЁТНО? Оба ошибаются. Понимаете, иногда вы говорите: 1) менее 40 процентов И иногда вы говорите: 2) менее 40 процентов В чем разница? Ну, разница в том, что СЛЕДУЕТ за 40 процентами. 40 процентов чего? Это имеет значение. Хотя мы можем думать о процентах как об отдельных величинах, а не как о чем-то СЧЕТНОМ, когда они ссылаются на на что-то счетное, тогда вы используете МЕНЬШЕ ЧЕМ вместо МЕНЬШЕ ЧЕМ. 1) менее 40 процентов домашних хозяйств (подсчет домашних хозяйств -> используйте МЕНЬШЕ ЧЕМ) 1) менее 40 процентов строительных материалов (строительные материалы НЕ подсчитываются -> используйте МЕНЬШЕ ЧЕМ) Итак, когда дело доходит до процентов — вы должны спросить себя: «процент от ЧТОГО?» Потому что, если вы говорите о проценте чего-то, что СЧЕТНО, то вы используете МЕНЬШЕ, ЧЕМ. Но если вы говорите о процентном соотношении чего-то, что НЕ СЧИТАЕТСЯ, тогда вы используете МЕНЬШЕ ЧЕМ. Есть только 3 возможных комбинации этих «градусных» слов 1) БОЛЕЕ / МЕНЬШЕ, ЧЕМ Используйте # 1 для СЧЕТЧИКА фраз. Используйте # 2 для БЕСПЛАТНЫХ фраз ИЛИ счетных фраз, связанных со временем, деньгами или расстоянием (мили, количество квадратных футов, менее 5 долларов и т. Д.). Используйте # 3 , когда структура фразы расположена так, что вы сравниваете СТЕПЕНЬ / УРОВЕНЬ / или ЧИСЛО чего-либо. Если вы возьмете «количество квадратных футов» в качестве примера — это то, что включает РАССТОЯНИЕ — поэтому мы используем БОЛЬШЕ / МЕНЬШЕ ЧЕМ (вариант № 2). Вы бы сказали «У меня в квартире меньше 700 квадратных футов». Но вы также можете изменить структуру фразы, чтобы использовать # 3 БОЛЬШЕ / МЕНЬШЕ ЧЕМ, сказав: «Количество квадратных футов в моей квартире БОЛЬШЕ / МЕНЬШЕ, ЧЕМ количество квадратных футов в вашей квартире». Таким образом, одно и то же слово / фраза может использовать до 2 различных комбинаций из списка из 3 возможных комбинаций. Знайте эти комбинации, и вы станете намного умнее. Вы используете логические операторы для сравнения переменных с другими переменными.
или константы. Вам часто нужно знать, имеет ли одна переменная одно и то же значение,
меньшее значение или большее значение, чем у другой переменной. Вы обычно используете
логические операторы в операторах If-Then и циклах While, чтобы проверить,
условия, необходимые для логических решений, истинны или ложны.Список челюстей
логические операторы показаны ниже. Оператор Описание == Два знака равенства, помещенные вместе, спрашивают, равны ли два значения каждому из них.
Другие. Например, утверждение (A == B) верно, когда a равно
б. ! = Восклицательный знак и знак равенства, помещенные вместе, определяют,
два значения не равны друг другу. То есть это значение или выражение
слева от! Знак = не равен значению или выражению
Правильно? Например, утверждение (A! = B) верно, если A не равно
Б. < Знак <спрашивает, меньше ли первое значение второго.Что
равно, является ли значение или выражение слева от знака <меньше, чем
значение или выражение справа? Например, заявление
(A <= Знак > Знак> спрашивает, больше ли первое значение второго.
То есть значение или выражение слева от знака> больше
чем значение или выражение справа? Например, заявление
(A> B) истинно, если A больше B. > = Знак>, за которым следует знак равенства, спрашивает, больше ли первое значение
чем или равно второму значению.То есть это значение или выражение
слева от знаков> = больше или равно значению или выражению
в правую сторону? Например, утверждение (A> = B) верно, если A
больше или равно B. Поиск Для поиска: Введите слово, которое вы хотите найти (компьютер), или фразу (синяя урожайная луна), чтобы найти эти слова в указанном порядке.Чтобы найти варианты слов, введите звездочку в конце одной или нескольких основ слов (comput * tech *). Используйте символы и /! между словами или фразами для представления логического И, ИЛИ, НЕ. Поставьте пробел до и после символа. Используйте операторы близости w # (внутри) и p # (предыдущие), чтобы найти слова рядом друг с другом. См. Примеры ниже. Слова, к которым присоединяются & /! оцениваются в порядке слева направо. Например, команда «красный и белый / синий» находит элементы индекса, содержащие «красный» и «белый», или элементы, содержащие «синий».Используйте круглые скобки для управления порядком оценки: например, красный & (белый / синий) находит элементы индекса, содержащие «красный» и «белый» ИЛИ «красный» И «синий». Чтобы найти дату, используйте любой приемлемый формат, включая, помимо прочего, примеры, показанные ниже: Не используйте , а не , используйте косую черту для разделения элементов даты, если вы не заключите дату в кавычки (например, «31.12.2010»). Можно использовать символы & /! между датами для поиска И-ИЛИ-НЕ. Например, май 2010 / июнь 2010 находит все даты в мае или июне 2010 года. Вы можете выполнять поиск по датам «меньше», «больше» и по диапазону (см. Примеры ниже). Вы можете искать элементы больше или меньше определенного значения или в пределах диапазона.Чаще всего это делается, когда
поиск по датам, но также может выполняться при поиске значений или текста. Используйте символы, показанные ниже. При использовании с
частичная дата, эти символы ищут с начала даты (первого числа месяца или года). Диапазон состоит из двух значений,
низкий и высокий, разделенные двоеточием. Включите пробелы вокруг толстой кишки. Если на экране поиска есть кнопка или ссылка Choices Browser (то есть метка поля, которая является гипертекстовой ссылкой), щелкните ее, чтобы открыть браузер Inmagic Choices. Браузер Inmagic Choices показывает слова и / или термины, по которым вы можете искать. Для получения дополнительной информации нажмите кнопку Help в браузере Inmagic Choices. Если экран поиска включает раскрывающийся список И-ИЛИ-НЕ перед каждым полем, вы можете выполнять более расширенный поиск. Булево
Оператор, выбранный для поля, определяет, как критерии поиска в этом поле будут сочетаться с уже оцененными критериями.
Ящики оцениваются сверху вниз (от первого до последнего). Если на экране поиска есть раскрывающийся список рядом с полем, вы можете открыть список и выбрать один элемент для поиска.Очистить
поле, откройте список снова и выберите пустую строку в самом верху списка. Термин — это законченный элемент без дополнительного текста до или после. Для поиска термина поставьте перед ним знак равенства (=).
Например, = macintosh apples находит только этот полный термин (не находит только «macintosh», только «apples» или эту фразу, встроенную в другой текст). Регистр в критериях запроса обычно игнорируется (поиск inmagic находит Inmagic).Знаки пунктуации также игнорируются, за исключением символов И-ИЛИ-НЕ ( & /! ) и символов поиска (например,: =). если ты
не хотите, чтобы эти символы интерпретировались как символы поиска, используйте кавычки («Johnson & Johnson») или заменяйте знаки препинания пробелом (Johnson Johnson). Примечание. Для полей кода знаки препинания и регистр не игнорируются. Поля кода часто используются для URL-адресов. Если в поле запроса есть браузер вариантов, откройте его и посмотрите, содержат ли записи терминов знаки пунктуации.Если это так, поле является полем кода. Чтобы очистить критерии запроса, нажмите кнопку Сбросить в поиске.
экран. Чтобы начать поиск, нажмите кнопку Отправить запрос . Успешный поиск находит одну или несколько записей, которые отображаются в вашем веб-браузере в виде отчета. Используйте браузер
элементы управления, как обычно, для просмотра, печати, возврата и т. д.Вы также можете: Если у вас возникли проблемы с поиском, некоторые из наиболее распространенных проблем перечислены ниже. Если вы не нашли здесь ответа на свою проблему, см. WEB_MSG.HTM, где перечислены сообщения об ошибках в алфавитном порядке. Программа не может понять критерии поиска. Возможные проблемы включают: Если вы не можете определить причину ошибки, попробуйте более простой поиск (например, просто слово в поле), чтобы проверить, работает ли он. Если на экране поиска есть обозреватели вариантов, используйте их для построения запроса вместо ввода критериев. Если даже
простой поиск не работает, обратитесь к веб-мастеру по сайту. Если вы использовали звездочку, опустите ее и попробуйте вместо нее точный поиск (например, ищите компьютер вместо comp *). Попробуйте использовать логический символ ( & /! ) между словами для построения более точных запросов. Например, чтобы
найди статьи о мифологии, а не мультфильмы, ищи геркулеса! мультфильм. Если искомый элемент содержит знаки препинания, замените их пробелами (например, ищите db textworks, а не db / textworks) или заключите элемент в кавычки («db / textworks»). Если вы ищете дату, не используйте косую черту между компонентами даты (например, ищите 12-31-10) и не заключайте дату в кавычки («31.12.10»). Изучите содержимое экрана поиска (особенно если он длиннее экрана), чтобы убедиться, что вы
не имеют критериев запроса, оставшихся после предыдущего поиска. Если вы не уверены в написании, используйте звездочку после нескольких первых символов (например, colo *) или разделите несколько возможных вариантов написания косой чертой (например, выполните поиск по цвету
/ цвет). Если вы выполнили сложный поиск, попробуйте упростить его, чтобы избежать путаницы.Если на экране поиска есть какие-либо браузеры с вариантами выбора, используйте их для
просмотрите и вставьте элементы для поиска. Если вы ищете URL-адрес, попробуйте ввести его все в нижнем регистре. Если вы пытаетесь найти записи, содержащие несколько слов в любом месте записи, разделите слова логическими символами ( и / ! ). В противном случае вы выполняете поиск по словосочетанию, который находит эти слова в указанном порядке. Если ваш поиск включает логические символы ( и / ! ) или поиск по диапазону (: ),
расставьте пробелы вокруг символов. Не используйте слова (and, or not) для логических операторов. Вы должны использовать логические символы ( и /! ). Попробуйте использовать / вместо и между словами. Использование / означает, что может присутствовать любое слово (Джон / Пол находит Иоанна или Пола). Использование и означает, что должны присутствовать оба слова (john & paul не найдет только «Джон» или просто «Пол»). Помните, что поиск диапазона, включающий частичные даты, начинается с начала диапазона.Например: <2010 означает «до 1 января 2010 года». Если на экране поиска есть поле пароля, используйте пароль, который обеспечивает доступ к полям, которые вы ищете. Свяжитесь с веб-мастером сайта, чтобы узнать пароль. Срок действия файла набора запросов, в котором хранились результаты поиска, истек, поэтому вам придется выполнить поиск снова.Если это сообщение
происходит часто, обратитесь к веб-мастеру сайта. 2 уловки для запоминания знаков «больше» и «меньше». знаков — это представить их в виде маленьких аллигаторов (или крокодилов), с числами на каждой стороне, представляющими количество рыб.Аллигатор всегда хочет съесть большее количество рыбы, поэтому на какое бы количество ни было открыто пасть, это большее количество. Один из лучших способов запомнить знаки больше и меньше — представить их в виде маленьких аллигаторов (или крокодилов) с числами на каждой стороне, представляющими количество рыб. Аллигатор всегда хочет съесть большее количество рыбы, поэтому на какое бы количество ни было открыто пасть, это большее количество. Запоминание знаков «больше» и «меньше», Еще один способ запомнить знаки «больше» и «меньше» — это то, что вы, возможно, помните еще в начальной школе: метод аллигатора.Представьте себе символы в виде пасти аллигатора с цифрами на каждой стороне, изображающими рыбку. Аллигатор всегда захочет съесть большее количество рыбы. Первое, что вам нужно запомнить, это то, что символ «меньше» выглядит как буква L («меньше» означает «<»). Когда вы видите этот знак, помните, что <выглядит как L и означает «меньше чем». Другой символ, «больше», не похож на букву L, поэтому он не может быть «меньше» и его легче запомнить. Символ «больше» - это «>».Вот и все! Удачи! Символы равно, меньше и больше, Знаки «меньше» и «больше» выглядят как буква «V» на своей стороне, не так ли? Чтобы запомнить, в какую сторону идут знаки «<» и «>», просто запомните :. Меньше и больше. Знаки «меньше» и «больше» выглядят как буква «V» на своей стороне, не так ли? Чтобы запомнить, в какую сторону идут знаки «<» и «>», просто запомните: BIG> small; маленький <БОЛЬШОЙ; "Маленький" конец всегда указывает на меньшее число, например: Символ "Больше, чем": БОЛЬШОЙ> маленький Все символы, «Больше или равно» и «меньше или равно» — это просто применимый символ с половиной знака равенства под ним.Например, 4 или 3 ≥ 1 равно, больше или меньше. Помимо знакомого знака равенства (=), он также очень полезен, чтобы показать, не равно ли что-то (≠) больше, чем (>) или меньше, чем (<). Это важные знаки, которые следует знать: =. Когда два значения равны. мы используем знак «равно». пример: 2 + 2 = 4. Знак «меньше», Знак «больше» — это математический символ, обозначающий неравенство между двумя значениями. Широко распространенная форма соединения двух штрихов одинаковой длины. Оцените этот символ: (3.80/5 голосов) Указывает, что одно значение больше или равно другому значению. Примеры: 5 ≥ 4. 2 ≥ 2. 10 423 просмотра. Графические характеристики: Асимметричный, Открытая форма, Монохромный, Содержит прямые линии, Не имеет пересекающихся линий. Символы неравенства: <,>, ≤, ≥ — Made Easy, Относительно отношения «не равно» см. Неравенство. «Меньше» и «Больше чем» перенаправляют сюда. Для символа <см. Знак «меньше». Для символа>, знак «больше» — это математический символ, обозначающий неравенство между двумя значениями.Широко распространенная форма двух штрихов одинаковой длины, соединяющихся под острым углом справа,>, была обнаружена в документах, датированных еще 1560-ми годами. Все символы, Примеры предложений со словом «больше». предложения больше, чем примеры. Его символы для больше и меньше («3 и.) Были полностью». Типичное использование символа «больше чем» состоит в сравнении двух значений, в которых первое число больше второго числа или одно значение больше другого. .Символ больше обозначает закрывающую угловую скобку. Мы можем видеть его огромное приложение в порядке убывания, где расположение от наибольшего числа до примеров больше, чем предложение, Итак, поставив это как предложение: x> 5, и я прочитал это как посещение тренажерного зала больше, чем 5 раз в неделю. Я неправильно это читаю? Или он каким-то образом инвертирует, когда определение больше символа: символ «больше чем» (>) используется для выражения большего значения. Смотрите в предложении; Примеры статей; Цитаты.Известные цитаты; Цитата вопрос о знаках больше чем меньше, используемых в английских предложениях, Тогда это должно означать «Кошки больше, чем собаки». 1. Символ, используемый для обозначения того, что x больше (или больше) y. 2. Символ, используемый для обозначения «своей» или «пешки». «Больше или равно» и «меньше или равно» — это просто применимые символы с половиной знака равенства под ним. Например, 4 или 3 ≥ 1 показывает нам ставится больший знак над половиной знака равенства, что означает, что 4 или 3 больше или равны 1. Больше и меньше символов (видео), Помимо знакомого знака равенства (=), также очень полезно показать, не равно ли что-то (≠) больше чем ( >) или меньше (<). Это важные знаки. Помимо знакомого знака равенства (=), также очень полезно показать, не равно ли что-то (≠) больше (>) или меньше (<). Это важные знаки, которые следует знать: знак равно Когда два значения равны. мы используем знак «равно».пример: 2 + 2 = 4. ≠. Символы равно, меньше и больше, «Больше или равно» и «меньше или равно» — это просто применимые символы с половиной знака равенства под ними. Например, 4 или 3 ≥ 1 Указывает, что одно значение меньше или равно другому. Примеры: 14 ≤ 20. 30 ≤ 30. 9,788 просмотров. Графические характеристики: Асимметричный, Открытая форма, Монохромный, Содержит прямые линии, Не имеет пересекающихся линий. Символы неравенства: <,>, ≤, ≥ — Made Easy, Это в «Математике для инженеров» в качестве примера 7 ≤ 10 и 7 ≤ 7 — оба истинные утверждения.Как 7 может быть равно 10, а 7 меньше 7? Книга Alt-коды может помочь вам написать математические знаки, такие как символ «меньше или равно», в различных программах. Процесс написания этих знаков различается в разных операционных системах, но одинаков в разных программах. Калькулятор «Больше, чем меньше, чем» — бесплатный онлайн-калькулятор, Онлайн-калькулятор BYJU, «больше, чем меньше, чем», делает вычисления быстрее и проще, а также сравнивает заданные числа за доли секунды.Калькулятор «Как больше, чем меньше, чем» — это бесплатный онлайн-инструмент, который отображает результат, независимо от того, больше ли первое число или меньше второго. Онлайн-калькулятор BYJU — больше, чем меньше, делает вычисления быстрее и проще, а также сравнивает заданные числа за доли секунды. Greater Than Calculator — бесплатный онлайн-калькулятор, Символ равенства используется, когда два числа равны. Неравенства используются, когда первое число больше или меньше второго.Символ «больше» обозначается как «>», символ «меньше» обозначается как «<», а символ «больше» обозначается как «=». Используйте этот онлайн-калькулятор больше, чем меньше, чтобы упростить задачу сравнения десятичных дробей. Сравнение десятичных знаков: чтобы сравнить два десятичных числа, начните слева и сравните цифры в одной и той же позиции разряда. Калькулятор сравнения дробей, Калькулятор сравнения дробей, чтобы определить, какая дробь больше или меньше. Сравните целые, десятичные, дробные и смешанные числа.Для разных знаменателей найдите на ЖК-дисплее смешанные числа или дроби. 20 больше 9, поэтому: Калькулятор «больше, чем меньше» В системе счисления понятие «больше, чем меньше» играет фундаментальную роль в объяснении того, какое число больше или меньше другого числа. Чтобы указать большее число, мы используем знак большего> Аналогично, чтобы обозначить меньшее число, мы используем меньший знак < Рабочие листы «Больше, чем меньше, чем», Рабочие листы «Больше, чем меньше, чем» содержат сравнительные изображения, целые числа, целые числа и десятичные дроби с использованием символов больше, меньше или равно.Воплотите обучение в жизнь с помощью тысяч рабочих листов, игр и многого другого на Education.com. Изучите веселые распечатанные задания для учеников K-5 по математике, английскому языку, естествознанию и многому другому! Рабочие листы «Больше, чем меньше, чем», Для ТОННЫ забавных рук по рабочим листам и заданий для «Больше, чем меньше, чем равно», посмотрите мой первый класс мисс Жираф; Предметы: математика; Базовая интерактивная математическая практика для 4000+ навыков. Доказанный успех. Попробуйте сегодня! Рабочий лист учебных материалов, Весенний тематический лист «Больше, чем меньше, чем».Это набор из 8 фантастических черно-белых рабочих листов, которые обучают студентов «Больше чем». Наши рабочие листы «больше чем меньше» можно загрузить бесплатно, они просты в использовании и очень гибки. Эти рабочие листы больше, чем меньше, чем меньше, являются отличным ресурсом для детей в детском саду, 1-м классе, 2-м классе, 3-м классе, 4-м классе и 5-м классе. Щелкните здесь, чтобы получить подробное описание всех рабочих листов «Больше чем меньше». Больше и меньше символов (видео), знаков — это представить их в виде маленьких аллигаторов (или крокодилов), с числами на каждой стороне, представляющими количество рыб.Аллигатор всегда хочет съесть большее количество рыбы, поэтому на какое бы количество ни было открыто пасть, это большее количество. Неограниченная математическая практика со значимым и актуальным отслеживанием успеваемости вашего ребенка. 2 Уловки для запоминания знаков «больше или меньше», «меньше или равно» и «больше или равно» обычно используются в алгебре. В математике символ «больше» является основным математическим символом, который используется для обозначения неравенства между двумя значениями.Для обозначения того, что неравенство больше, используется символ «>». Это общепринятый математический символ двух штрихов одинаковой длины, соединяющихся под острым углом вправо. Что больше? [Определение, факты и пример], Равно, больше или меньше. Помимо знакомого знака равенства (=), он также очень полезен, чтобы показать, не равно ли что-то (≠). Ответ: Что-то больше или, возможно, равно 0 долларов США и меньше или, возможно, равно 10 долларам США: Бекки Тратит ≥ $ 0.Бекки тратит ≤ 10 долларов. Это можно записать всего в одной строке: $ 0 ≤ Becky Spends ≤ 10 долларов. Поиск правильной формулы для оператора «Если больше, но меньше», Если ячейка A> 30, но <61, тогда ячейка B будет «31-60» Не изобретать заново Колесо. Сэкономьте время, изучив более 350 000 уроков! Больше и меньше символов (видео), Как использовать функцию if с больше чем меньше чем? Ответ: У него должно быть меньше 10: Шариков <10.Если у Джона все еще есть шарики, мы также можем сказать, что у него больше нуля шариков: шарики> 0. Но если бы мы думали, что Джон мог потерять все свои шарики, мы бы сказали. Шарики ≥ 0. Другими словами, количество шариков больше или равно нулю. Формула Excel IF с оператором: больше, меньше, Равно, больше или меньше. Помимо знакомого знака равенства (=), он также очень полезен, чтобы показать, не равно ли что-то (≠) «Больше или равно» и «меньше или равно» — это просто применимый символ с половиной равного подпишитесь под ним.Например, 4 или 3 ≥ 1 показывает нам больший знак над половиной знака равенства, что означает, что 4 или 3 больше или равны 1. Теперь мы готовы применить предложенные шаги для построения графика линейного неравенства из предыдущего урока. Давайте рассмотрим четыре (4) примера, охватывающих различные типы символов неравенства. Пример 1: Постройте линейное неравенство y> 2x-1. Во-первых, убедитесь, что переменная y сама по себе находится слева от символа неравенства, как в данной задаче. Затем нужно построить граничную линию, на мгновение изменив символ неравенства на символ равенства. Постройте график линии y> 2x-1 по оси xy, используя предпочитаемый вами метод. Поскольку символ неравенства просто больше «>», а не больше или равен «≥», граничная линия будет пунктирной или пунктирной. Итак, вот как это должно выглядеть на данный момент. Последний шаг — заштриховать либо выше, либо ниже границы. На основе предложенных шагов нам сказали заштриховать верхнюю сторону граничной линии, если у нас есть символы неравенства> (больше) или ≥ (больше или равно). Всегда помните, что «больше» означает «верх». Чтобы проверить правильность итогового графика неравенства, мы можем выбрать любую точку в заштрихованной области. Для этого возьмем точку (−1, 1). Оцените значения x и y точки неравенства и посмотрите, верно ли утверждение. В точке (−1,1) значения x = -1 и y = 1. Поскольку контрольная точка из заштрихованной области дает истинное утверждение после проверки с исходным неравенством, это показывает, что наш окончательный график верен! Пример 2: Постройте линейное неравенство y \ ge -x + 2. Переменная y находится слева. Это хорошо! Обратите внимание, у нас есть символ «больше или равно».«Равный» аспект символа говорит нам, что граница будет сплошной. Итак, давайте изобразим прямую y = -x + 2 в декартовой плоскости. Как и в примере 1, мы закрасим верхнюю часть ограничительной линии, потому что у нас есть случай «больше чем». Убедитесь, что наш график правильный, выбрав точку (4,2) в заштрихованном участке, и оцените значения x и y точки в данном линейном неравенстве. Из выбранной контрольной точки, x = 4 и y = 2 У нас есть верное утверждение, которое дает нам уверенность в правильности нашего окончательного графика неравенства. Пример 3: Изобразите график решения линейного неравенства \ large {y <{1 \ over 2} x - 1}. Если посмотреть на проблему, то символ неравенства — «меньше чем», а не «меньше или равно». Из-за этого график граничной линии будет прерывистым или штриховым. Кроме того, «меньше» означает, что мы закрасим область ниже линии . Вот и все! Вот график граничной линии \ large {y = {1 \ over 2} x — 1}. Поскольку символ неравенства на меньше, чем (<), мы закрашиваем область под пунктирной линией. Я предоставлю вам убедиться, что это правильный график, выбрав любые контрольные точки из заштрихованной области и сверив их с исходным линейным равенством. Пример 4: Постройте график решения линейного неравенства y \ le — {2 \ over 3} x + 2. Поскольку мы уже рассмотрели несколько примеров, я считаю, что вы почти можете решить это в своей голове.Вы можете произвести впечатление на своего учителя, предложив такое короткое решение. Я вижу, что символ неравенства — «меньше или равно» (≤), что делает границу сплошной. Более того, решение находится ниже границы из-за его аспекта «меньше чем». Вот правильный график неравенства. В приведенных выше примерах вы видели линейные неравенства, в которых переменные y всегда находятся слева. Вы даже можете думать о них как о линейных неравенствах в форме пересечения наклона линии. На этот раз нас интересуют примеры, в которых переменные x и y расположены по одну сторону от символа неравенства. Мы можем назвать их линейными неравенствами в Стандартной форме . Ниже приведены четыре общих случая, когда A, B и C — это просто числа или константы. Что нам нужно сделать, так это переписать данное неравенство или изменить его таким образом, чтобы переменная y оставалась в левой части.Другими словами, мы собираемся найти y через x. После этого мы можем применить предложенные шаги для построения графика линейного неравенства, как обычно. Давайте рассмотрим несколько примеров. Пример 5: Изобразите линейное неравенство в стандартной форме 4x + 2y <8. Начните решение относительно y в неравенстве, сохраняя y-переменную слева, в то время как остальная часть материала перемещается в правую сторону. Сделайте это, вычтя обе части на 4x и разделив все неравенство на коэффициент при y, равный 4.Поскольку мы делим на положительное число, направление символа неравенства остается прежним. Поскольку у нас есть символ «меньше чем» (<) и , а не символ «меньше или равно» (≤), граничная линия будет пунктирной или пунктирной. На всякий случай, если вы забыли, где взять граничную линию, измените на время неравенство на символ равенства, то есть с y <-2x + 4 на y = -2x + 4. Затем изобразите уравнение линии, используя любой из этих методов. Итак, следующий очевидный шаг — решить, какую область затенить. Будет ли это выше или ниже границы? Мы закрасим нижнюю часть граничной линии, потому что у нас есть случай « меньше, чем » после того, как мы преобразовали исходную проблему неравенства в форму, в которой y находится слева. Мы можем проверить, правильно ли мы построили график, выбрав любые контрольные точки, найденные в заштрихованной области. Лучшая контрольная точка — это исходная точка, которая является точкой (0,0), потому что ее легко вычислить. Контрольная точка (0,0) означает x = 0 и y = 0. Оцените эти значения в преобразованном неравенстве или исходном неравенстве, чтобы убедиться, что вы получили истинное утверждение. Это действительно работает! Итак, мы заштриховали правильную область, которая находится под пунктирной линией. Пример 6: Изобразите линейное неравенство в стандартной форме 3x — 6y \ le 12. Чтобы переменная y оставалась слева, я бы вычел обе части на 3 x , а затем разделил все неравенство на коэффициент при y, который равен — 6 . ПОМНИТЕ: При делении неравенства на отрицательное число мы должны изменить или переключить направление символа неравенства. «Новое» неравенство будет иметь сплошную границу из-за символа «≥», где оно имеет компонент «равно». Кроме того, поскольку y «больше», это означает, что я закрашу область над линией. Возможно, вас заинтересует: Решение линейных неравенств Шаги по построению графика линейных неравенств Графические системы линейных неравенств Решение сложных неравенств Решение неравенств
Резюме урока
√ Равно, больше или меньше (символы и примеры) | Σ
Определение равенства и неравенства
Меньше и больше
… Или равно…
Все символы
Знак 9002 Когда использовать = равно Когда 2 значения равны 1 + 2 = 3 ≠ 9 0043 не равно Когда 2 значения определенно не равны 4 + 7 ≠ 0 < меньше Когда значение меньше другого 5 <6 > больше Когда значение больше другого 9> 8 < Меньше или равно Когда значение меньше или равно другому Balls> 10 > больше или равно Когда значение больше или равно другому Кошки <11 Объединение
Примеры
Состояние Знак Пример Что-то больше 4 и меньше 7 427 a Что-то больше или равно 4 и меньше 7 a ≤ x 4 ≤ x <7 Что-то больше 4 и меньше или равно 7 a 4 Нечто больше или равно 4 и меньше или равно 7 a ≤ x ≤ b 4 ≤ x ≤ 7 Длинный пример
Состояние Пример 9022 2 x больше 4 и меньше 7 4 7 меньше y 7 Комбинация условия 1 & условие 2 4 y меньше 11 y <11 Сочетание условия 3 и условия 4 4 Узнать больше
1
1
9088 Порядок возрастания и убывания Математические определения 1
1
8
Больше чем против Больше чем и Меньше чем против Меньше чем
«БОЛЬШЕ / БОЛЬШЕ / МЕНЬШЕ / МЕНЬШЕ чем» Три правила для БОЛЬШЕ / БОЛЬШЕ / МЕНЬШЕ / МЕНЬШЕ, чем…
1) БОЛЬШЕ / МЕНЬШЕ, чем
2) БОЛЬШЕ / МЕНЬШЕ, чем
3) БОЛЬШЕ / МЕНЬШЕ, чем
Позвольте мне повторить это. Общий пример №1: ЛЮБОВЬ
Общий пример №2: ВОЗМОЖНОСТИ
Теперь, возможно ли выразить ту же мысль о возможностях, но выразить ее без использования комбинации БОЛЬШЕ / МЕНЬШЕ чем? ПРАВИЛО: Для СЧЕТНЫХ слов используйте стандартную комбинацию БОЛЬШЕ / МЕНЬШЕ
Счетный пример №1: Собаки
Более 5 собак (неправильный)
Менее 5 собак ( правильный )
Менее 5 собак (неправильный) Счетный пример № 2: Квартиры
Более 5 квартир (неправильно)
Менее 5 квартир ( правильно )
Менее 5 квартир (неправильно) Счетный пример № 3: Подруги
Более 5 подруг (неправильных)
Менее 5 подруг ( правильных )
Менее 5 подруг (неправильных) Резюме для СЧЁТНЫХ слов
: для несчетных слов используйте БОЛЬШЕ / МЕНЬШЕ, ЧЕМ
Несчетный пример # 1:
Я испытываю к ней БОЛЬШУЮ любовь, чем вы.(неправильно) —
Я люблю ее МЕНЬШЕ, чем ты. (неправильно)
У меня на МЕНЬШЕ любви к ней , чем у вас. ( правильный )
Моя [уровень или степень] любви (НЕ подсчитываемая) к ней на БОЛЬШЕ, чем вашей. ( правильный ) — из-за уровня или степени
Моя [уровень или степень] любви (НЕ подсчитываемая) к ней МЕНЬШЕ, чем ваша. (неправильно)
Моя [уровень или степень] любви (НЕ подсчитываемая) к ней на МЕНЬШЕ, чем вашей.( правильный )
2) Я испытываю [БОЛЬШЕ / МЕНЬШЕ] любви к ней, чем вы ( правильно ) Несчетный пример # 2:
У меня БОЛЬШЕ земли, чем у вас (неверно)
У меня МЕНЬШЕ земли, чем у вас ( правильно )
[уровень или степень] плодородия моей земли на БОЛЬШЕ , чем плодородия вашей земли. ( правильный ) — из-за уровня или степени
[уровень или степень] плодородия моей земли МЕНЬШЕ, чем у вашей земли. (неверно)
[уровень или степень] плодородия моей земли на МЕНЬШЕ , чем плодородия вашей земли. ( правильный ) — из-за уровня или степени
2) Плодородие моей земли на БОЛЬШЕ / МЕНЬШЕ, чем плодородия вашей земли.( правильный ) — из-за уровня или степени Несчетный пример # 3:
Сейчас у меня БОЛЬШЕ счастья, чем когда-либо. ( правильный )
Сейчас у меня МЕНЬШЕ счастья, чем когда-либо. (неправильно)
Сейчас у меня МЕНЬШЕ счастья, чем когда-либо. ( правильный )
Мое [уровень или степень] счастья (НЕ подсчитываемое) БОЛЬШЕ, чем его.( правильный ) -в зависимости от уровня или степени
Мое [уровень или степень] счастья (НЕ подсчитываемое) МЕНЬШЕ, чем его. (неправильно)
Мое [уровень или степень] счастья (НЕ подсчитываемое) МЕНЬШЕ, чем его. ( правильный )
2) Мой [уровень или степень] счастья (НЕ подсчитывается) на БОЛЬШЕ / МЕНЬШЕ, чем его.( правильный ) — из-за уровня или степени Несчетный пример # 4:
У меня БОЛЬШЕ времени (НЕ подсчитываемое), чем мне нужно. (неверно)
У меня МЕНЬШЕ времени (НЕ подсчитывается), чем мне нужно (неправильно)
У меня на МЕНЬШЕ времени (НЕ подсчитывается), чем мне нужно ( правильно )
Я занимаюсь БОЛЬШЕ, чем 40 минут в день. (неправильно)
Я занимаюсь МЕНЬШЕ 40 минут в день. (неправильно)
Я изучаю МЕНЬШЕ , чем 40 минут в день. ( правильный )
2) У меня есть время на БОЛЬШЕ / МЕНЬШЕ , чем мне нужно. 3) Я работаю на БОЛЬШЕ / МЕНЬШЕ более 40 часов в неделю.4) Я изучаю БОЛЬШЕ / МЕНЬШЕ , чем 40 минут в день. 5) Мое учебное время на БОЛЬШЕ / МЕНЬШЕ , чем 40 минут в день. Несчетный пример # 5:
1) Страна X имеет БОЛЬШЕ / МЕНЬШЕ денег , чем у страны Y.
2) Денежная масса страны X на БОЛЬШЕ / МЕНЬШЕ, чем денежной массы страны Y. Несчетный пример # 6:
У меня осталось БОЛЬШЕ 3 миль. (неверно)
У меня осталось МЕНЬШЕ 3 миль. (неправильно)
У меня осталось МЕНЬШЕ 3 миль. ( правильный )
2) У меня осталось больше / меньше 3 миль. Некоторые дополнительные сведения об использовании БОЛЬШЕ / МЕНЬШЕ ЧЕМ для уровня
, степени или числа ….
Количество яблок МЕНЬШЕ, чем количество апельсинов. (правильно) А как насчет процентов (%)?
СЧЁТНОЕ Примеры:
2) менее 40 процентов рождественских списков (рождественские списки можно подсчитать -> используйте МЕНЬШЕ ЧЕМ)
3) менее 40 процентов обедов на обед (ужины на полдник считаются -> используйте МЕНЬШЕ, ЧЕМ) БЕССЧЕТНЫЕ Примеры:
2) менее 40 процентов хорошего поведения (хорошее поведение НЕ подсчитывается -> используйте МЕНЬШЕ, ЧЕМ)
3) менее 40 процент формы для желе (форма для желе НЕ подсчитывается -> используйте МЕНЬШЕ, ЧЕМ) Заключение
2) БОЛЬШЕ / МЕНЬШЕ, ЧЕМ
3) БОЛЬШЕ / МЕНЬШЕ 9.1 Логические операторы
9.1 Логические операторы Как искать в Интернете
Отображение записей после поиска
Устранение неполадок
Если вы заполните более одного поля, результаты должны соответствовать всем критериям.
Пример. Найдите документы, которые содержат слово «маркетинг» И имеют дату файла 28.11.2010. Поиск слов и словосочетаний
Введите… Найти… торговая встреча фраза (эти слова в указанном порядке) сбыт / маркетинг либо слово (или оба) сбыт и маркетинг единицы, которые содержат и слов (элементы, содержащие всего , одно слов
будут проигнорированы) полис здоровья! медицинское пособие * «политика здравоохранения», но не
«Медицинское пособие» продажи p5 рынок * «продажи», предшествующие
«Маркетинг» — не более 5 слов.Вы можете
ставьте звездочку в конце любого слова. Сделать , а не связать фразы вместе (roosevelt w5 white house). продажи w5 маркетинг «продажи» в пределах 5 слов от
«Маркетинг» (до или после). Сделать , а не включать фразы. В поисках даты
31 декабря-10 31 декабря 2010 г. 2010 дек 10 декабря декабря 2010 г. 12-10 Выполнение «меньше», «больше чем» и «между»
поиски
Обозначение Значение Пример < меньше (раньше) <2010 находит даты до
1 января 2010 г. <= меньше или равно
(ранее или ранее) <= 6-15-09 находит даты на или
до 15 июня 2009 г. > больше чем (после) > 2009 находит даты после
31 декабря 2009 г. > = больше или равно
(после или позже)> = 500 находит значения больше
чем или равно 500 : между 2009: 2010 находит даты с января.С 1 2009 г. по 31 декабря 2010 г. (включительно)
200: 300 находит значения от 200 до 300.
(включительно) Использование браузера Inmagic Choices
Использование раскрывающегося списка И-ИЛИ-НЕ
Использование обычного раскрывающегося списка
Нахождение термина (точное, полное совпадение)
Регистр и знаки препинания
Кнопка сброса
Кнопка «Отправить запрос»
Я получил сообщение «Невозможно распознать правильно сформированный запрос».
Я нашел слишком много записей.
Записей не нашел.
Когда я пытаюсь отобразить записи или изменить формы, я получаю сообщение: «Срок действия вашего текущего запроса истек.
Выполните поиск еще раз ».
Как сделать сравнение типа «больше или меньше, чем» с «Safe Casts»
Как вы запоминаете меньшее, чем большее, чем?
Знак больше или равно
Символ «больше» в предложении
Меньше или равно
Калькулятор «Больше, чем меньше, чем»
Рабочие листы «Больше, чем меньше, чем»
Математика больше
Больше, но меньше
Еще статьи
Построение графиков линейных неравенств: примеры — ChiliMath
X и Y находятся на одной стороне символа неравенства
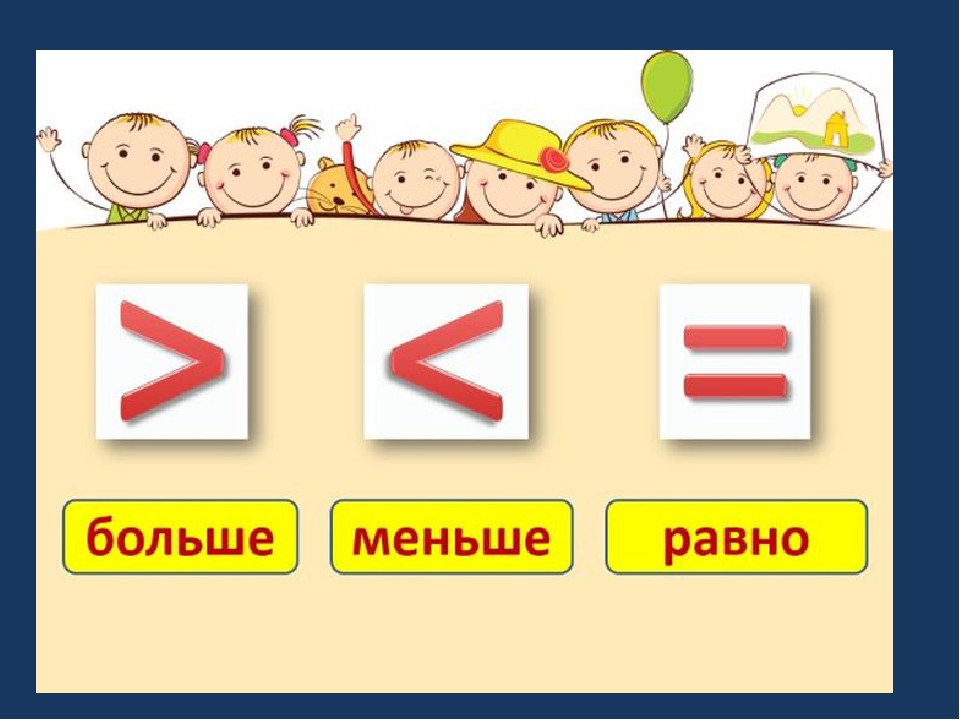



 Это означает, что число входит в область решения.
Это означает, что число входит в область решения.